模電·放大電路的分析方法—

放大電路的分析方法——等效電路法

晶體管的直流模型及靜態工作點的估算法
晶體管共射h參數等效模型
- $h$ 參數等效模型的由來
- 參數的物理意義
- 簡化的h參數等效模型
- ${r\tiny be}$ 的近似表達式
共射放大電路動態參數的分析

??晶體管電路分析的復雜性在于其特性的非線性，如果能在一定條件下將特性線性化，即用線性電路來描述其非線性特性，建立線性模型，就可應用線性電路的分析方法來分析晶體管電路了。針對應用場合的不同和所分析問題的不同，同一只晶體管有不同的等效模型。這里首先簡單介紹晶體管在分析靜態工作點時所用的直流模型;然后重點闡述用于低頻小信號時的 $h$ 參數等效模型，以及使用該模型分析動態參數的方法。

晶體管的直流模型及靜態工作點的估算法

$（ a ）基本共射放大電路$

$（ b ）直接耦合共射放大電路$

$（ c ）阻容耦合共射放大電路$
??在對上面基本共射放大電路、直接耦合共射放大電路、阻容耦合共射放大電路所示各共射放大電路進行靜態分析時，分別得出靜態工作點的下面三個表達式。當將 b - e 間電壓 $U\tiny BEQ$ 取一個固定數值時，也就是認為 b - e 間等效為直流恒壓源，說明已將晶體管輸人特性折線化，如下圖 ( a ) 晶體管的直流模型輸入特性折線化所示。式中集電極電流 ${I\tiny CQ}={\beta I\tiny BQ}$ ，說明 $I\tiny CQ$ 僅決定于 $I\tiny BQ$ 而與靜態管壓降 $U\tiny CEQ$ 無關，即輸出特性曲線是橫軸的平行線，如下圖 ( b ) 晶體管的直流模型輸出特性理想化所示，所以晶體管的直流模型如下圖 ( c ) 晶體管的直流模型輸出特性理想化所示。圖 ( c ) 中的理想二極管限定了電流方向。
$\begin{cases} {I\tiny BQ}=\frac{{V\tiny BB}-{U\tiny BEQ}}{R\tiny b} \\ {I\tiny CQ}={\={\beta}}{I\tiny BQ}={\beta}{I\tiny BQ} \\ {U\tiny CEQ}={V\tiny CC}-{I\tiny CQ}{R\tiny c} \end{cases}$

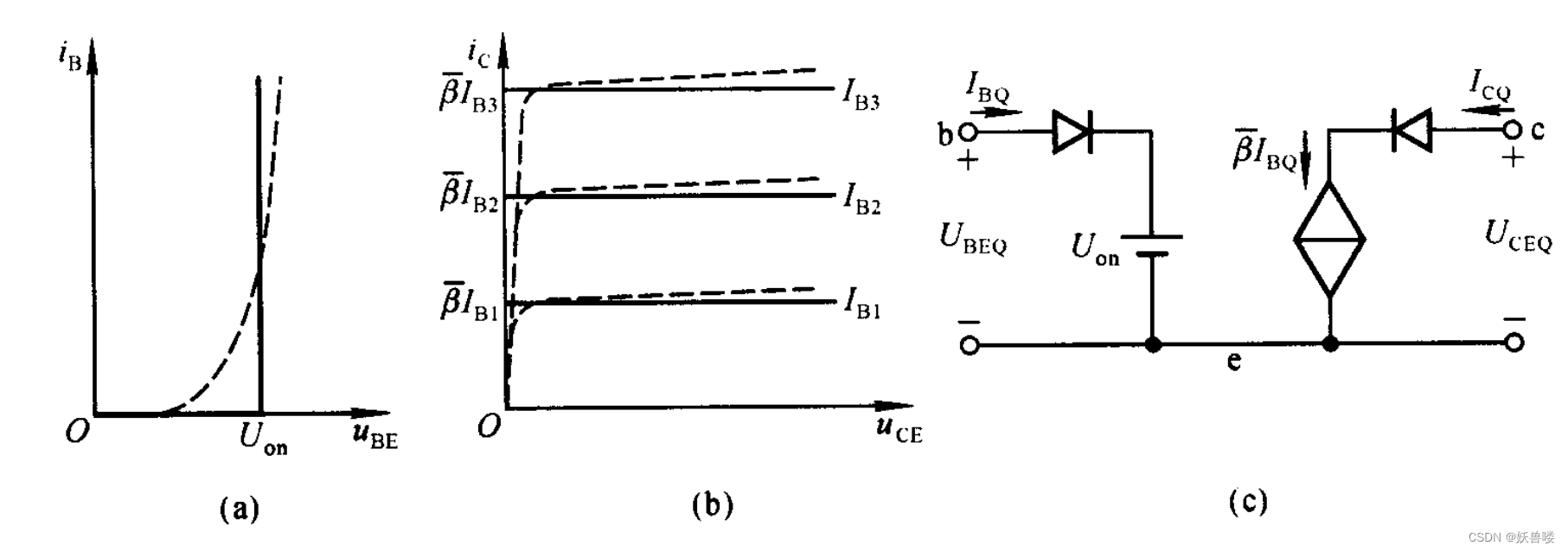
$晶體管的直流模型$ $（ a ）輸入特性折線化（ b ）輸出特性理想化（ c ）直流模型$
??應當特別指出，晶體管的直流模型是晶體管在靜態時工作在放大狀態的模型，它的使用條件是: ${U\tiny BE}＞{U\tiny on}$ 且 ${U\tiny CE}＞{U\tiny BE}$ ，并認為 ${\={\beta}}={\beta}$ 。
??在下圖阻容耦合共射放大電路所示中，若已知 ${V\tiny CC}=12V$ ， ${R\tiny b}=510kΩ$ ， ${R\tiny c}=510kΩ$ ；晶體管的 ${\beta}=0$ ， ${U\tiny BEQ}≈0.7V$ ，則根據 ${I\tiny BQ}=\frac{{V\tiny BB}-{U\tiny BEQ}}{R\tiny b}$ 可得， ${I\tiny BQ}≈22uA$ ， ${I\tiny CQ}≈2.2mA$ ， ${U\tiny CEQ}≈5.35V$ 。

$（ c ）阻容耦合共射放大電路$

晶體管共射h參數等效模型

??在共射接法的放大電路中，在低頻小信號作用下，將晶體管看成一個線性雙口網絡，利用網絡的 $h$ 參數來表示輸入端口、輸出端口的電壓與電流的相互關系，便可得出等效電路，稱之為共射 $h$ 參數等效模型。這個模型只能用于放大電路低頻動態小信號參數的分析。

$h$ 參數等效模型的由來

晶體管的共射h參數等效模型
$晶體管的共射 h 參數等效模型$ $（ a ）將晶體管看成線性雙口網絡（ b ）輸入特性曲線$ $（ c ）輸出特性曲線（ d ）共射 h 參數等效模型$
??若將晶體管看成一個雙口網絡，并以 b - e 作為輸入端口，以 c - e 作為輸出端口，如上圖 ( a ) 所示，則網絡外部的端電壓和電流關系就是晶體管的輸入特性和輸出特性，如上圖 ( b ) 、( c ) 所示。可以寫成關系式
$\begin{cases} {\large u\tiny BE}=f({i\tiny B},{\large u\tiny BE}) \\ {\large i\tiny C}=f({i\tiny B},{\large u\tiny BE}) \\ \end{cases}$

式中 ${\large u\tiny BE}$ 、 ${I\tiny B}$ 、 ${\large u\tiny CE}$ 、 ${i\tiny C}$ 均為各電量的瞬時總量。為了研究低頻小信號作用下各變化量之間的關系，對上邊兩式求全微分，得出

$\begin{cases} d{\large u\tiny BE}=\frac{\large ? u\tiny BE}{{\large ? i}{\tiny B}}{\huge \mid_{\small U\tiny CE}}di{\tiny B} +\frac{\large ? u\tiny BE}{{\large ? u}{\tiny CE}}{\huge \mid_{\small I\tiny B}}d{\large u}{\tiny CE}\\ \\ d{\large i\tiny C}=\frac{\large ? i\tiny C}{{\large ? i}{\tiny B}}{\huge \mid_{\small U\tiny CE}}di{\tiny B} +\frac{\large ? i\tiny C}{{\large ? u}{\tiny CE}}{\huge \mid_{\small I\tiny B}}d{\large u}{\tiny CE}\\ \end{cases}$

??由于 ${\large du}{\tiny BE}$ 代表 ${\large u}{\tiny BE}$ 的變化部分，可以用 ${\.{U}}{\tiny be}$ 取代；同理 ${\large di}{\tiny B}$ 可用 ${\.{I}}{\tiny b}$ 取代， ${\large di}{\tiny C}$ 可用 ${\.{I}}{\tiny c}$ 取代， ${\large du}{\tiny CE}$ 可用 ${\.{U}}{\tiny ce}$ 取代。根據電路原理網絡分析知識，可從上面兩式子得出 $h$ 參數方程
$\begin{cases} {\.{U}}{\tiny be}={h\tiny 11e}{\.{I}}{\tiny b}+{h\tiny 12e}{\.{U}}{\tiny ce} \\ {\.{I}}{\tiny c}={h\tiny 21e}{\.{I}}{\tiny b}+{h\tiny 22e}{\.{U}}{\tiny ce} \\ \end{cases}$
下標e表示共射接法，式中
$\begin{cases} {h\tiny 11e}=\frac{\large ? u\tiny BE}{{\large ? i}{\tiny B}}{\huge \mid_{\small U\tiny CE}} \\ \\ =\frac{\large ? u\tiny BE}{{\large ? u}{\tiny CE}}{\huge \mid_{\small I\tiny B}} \\ \\ =\frac{\large ? i\tiny C}{{\large ? i}{\tiny B}}{\huge \mid_{\small U\tiny CE}}\\ \\ =\frac{\large ? i\tiny C}{{\large ? u}{\tiny CE}}{\huge \mid_{\small I\tiny B}} \\ \\ \end{cases}$

?? ${\.{U}}{\tiny be}={h\tiny 11e}{\.{I}}{\tiny b}+{h\tiny 12e}{\.{U}}{\tiny ce}$ 表明，電壓 ${\.{U}}{\tiny be}$ 由兩部分組成：
第一項表示由 ${\.{I}}{\tiny b}$ 產生一個電壓，因而 ${h\tiny 11e}$ 為一電阻；
第二項表示由 ${\.{U}}{\tiny ce}$ 產生一個電壓，因而 ${h\tiny 12e}$ 無量綱；所以 b - e 間等效成一個電阻與一個電壓控制的電壓源串聯。
?? ${\.{I}}{\tiny c}={h\tiny 21e}{\.{I}}{\tiny b}+{h\tiny 22e}{\.{U}}{\tiny ce}$ 表明，電流 ${\.{I}}{\tiny c}$ 也由兩部分組成：
第一項表示由 ${\.{I}}{\tiny b}$ 控制產生一個電流，因而 ${h\tiny 21e}$ 無量綱;
第二項表示由 ${\.{U}}{\tiny ce}$ 產生一個電流，因而 ${h\tiny 22e}$ 為電導；所以 c - e 間等效成一個電流控制的電流源與一個電阻并聯。
??這樣，得到晶體管的等效模型如下圖所示。由于 ${h\tiny 11e}$ 、 ${h\tiny 12e}$ 、 ${h\tiny 21e}$ 、 ${h\tiny 22e}$ 四個參數的量綱不同，故稱為 $h$ （混合)參數，由此得到的等效電路稱為h參數等效模型。
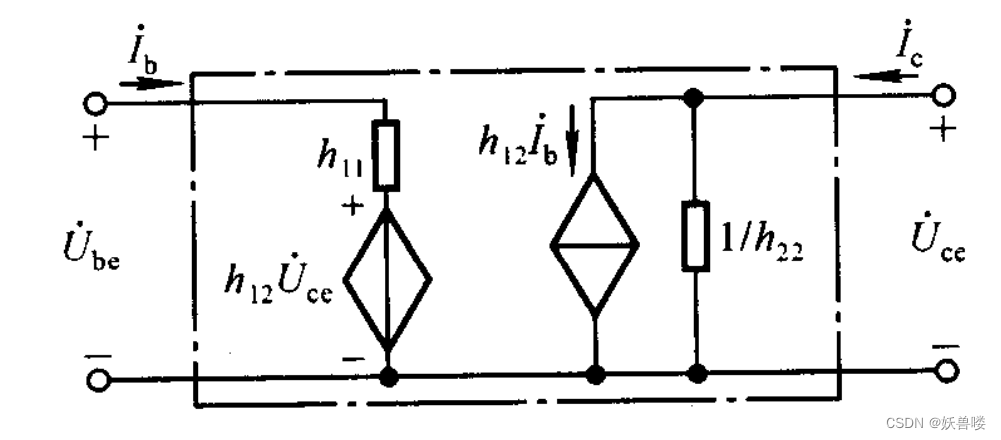
晶體管的共射h參數等效模型
$晶體管的共射 h 參數等效模型$

參數的物理意義

??研究 $h$ 參數與晶體管特性曲線的關系，可以進一步理解它們的物理意義和求解方法。

?? ${h\tiny 11e}$ 是當 ${\large u}{\tiny CE}={U\tiny CEQ}$ 時 ${\large u}{\tiny BE}$ 對 ${i\tiny B}$ 的偏導數。從輸入特性上看，就是 ${\large u}{\tiny CE}={U\tiny CEQ}$ 那條輸人特性曲線在Q點處切線斜率的倒數。小信號作用時， ${h\tiny 11e}=\frac{\large ? u\tiny BE}{{\large ? i}{\tiny B}}≈\frac{\large \Delta u\tiny BE}{\large \Delta i\tiny B}$ ，見下圖所示。因此 ${h\tiny 11e}$ 表示小信號作用下 b - e 間的動態電阻，常記作 ${\large r\tiny be}$ 。Q點越高，輸入特性曲線越陡， ${h\tiny 11e}$ 的值也就越小。
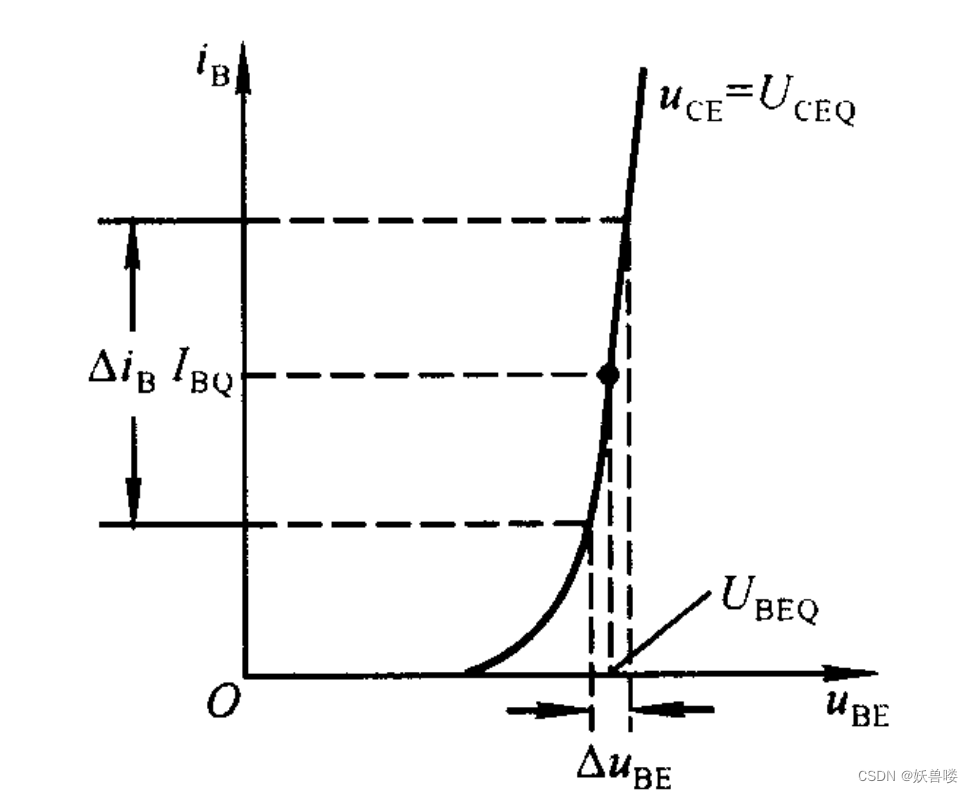
h參數的物理意義及求解方法——求解h11e
$h參數的物理意義及求解方法——求解{h\tiny 11e}$
?? ${h\tiny 12e}$ 是當 ${\large i}{\tiny B}={I\tiny BQ}$ 時 ${\large u}{\tiny BE}$ 對 ${\large u}{\tiny CE}$ 的偏導數。從輸人特性上看，就是在 ${\large i}{\tiny B}={I\tiny BQ}$ 的情況下 ${\large u}{\tiny CE}$ 對 ${\large u}{\tiny BE}$ 的影響，可以用 $\frac{\large \Delta u\tiny BE}{\large \Delta u\tiny CE}$ 求出 ${h\tiny 12e}$ 的近似值，見下圖所示。 ${h\tiny 12e}$ 描述了晶體管輸出回路電壓 ${\large u}{\tiny CE}$ 對輸入回路電壓 ${\large u}{\tiny BE}$ 的影響，故稱之為內反饋系數。當 c - e 間電壓足夠大時，如 ${U}{\tiny CE}≥1V$ ， $\frac{\large \Delta u\tiny BE}{\large \Delta u\tiny CE}$ 的值很小，多小于 $10^{-2}$ 。
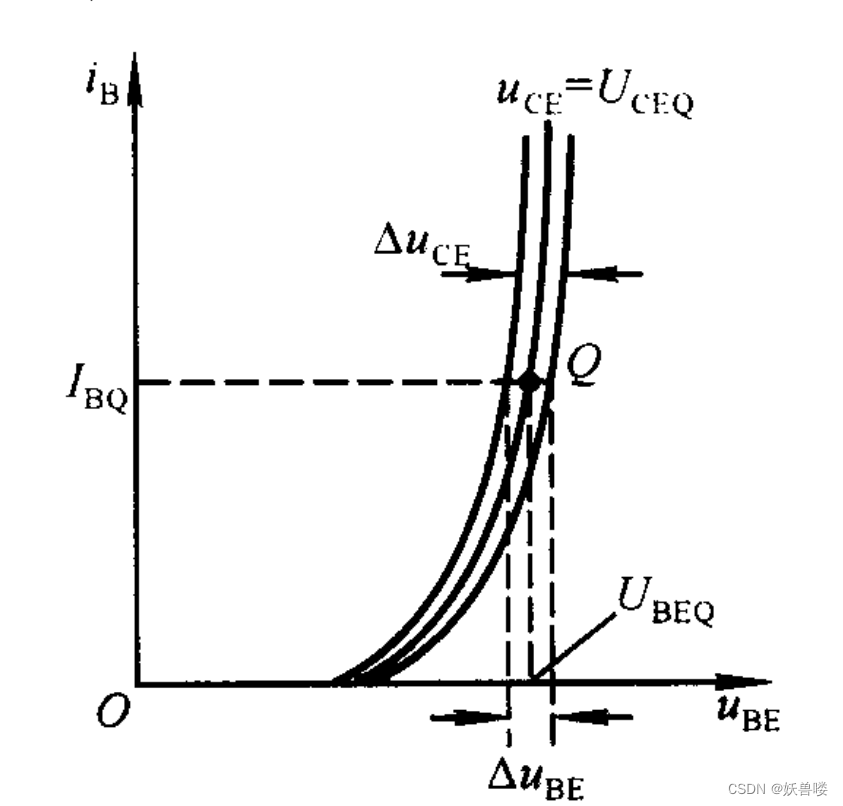
h參數的物理意義及求解方法——求解h12e
$h參數的物理意義及求解方法——求解{h\tiny 12e}$

?? ${h\tiny 21e}$ 是當 ${\large u}{\tiny CE}={U\tiny CEQ}$ 時 ${i\tiny C}$ 對 ${i\tiny B}$ 的偏導數。從輸出特性上看，當小信號作用時， ${h\tiny 12e}=\frac{\large ? i\tiny C}{{\large ? i}{\tiny B}}≈\frac{\large \Delta i\tiny C}{{\large \Delta i}{\tiny B}}$ ，見下圖所示。所以， ${h\tiny 21e}$ 表示晶體管在Q點附近的電流放大系數 $\beta$ 。
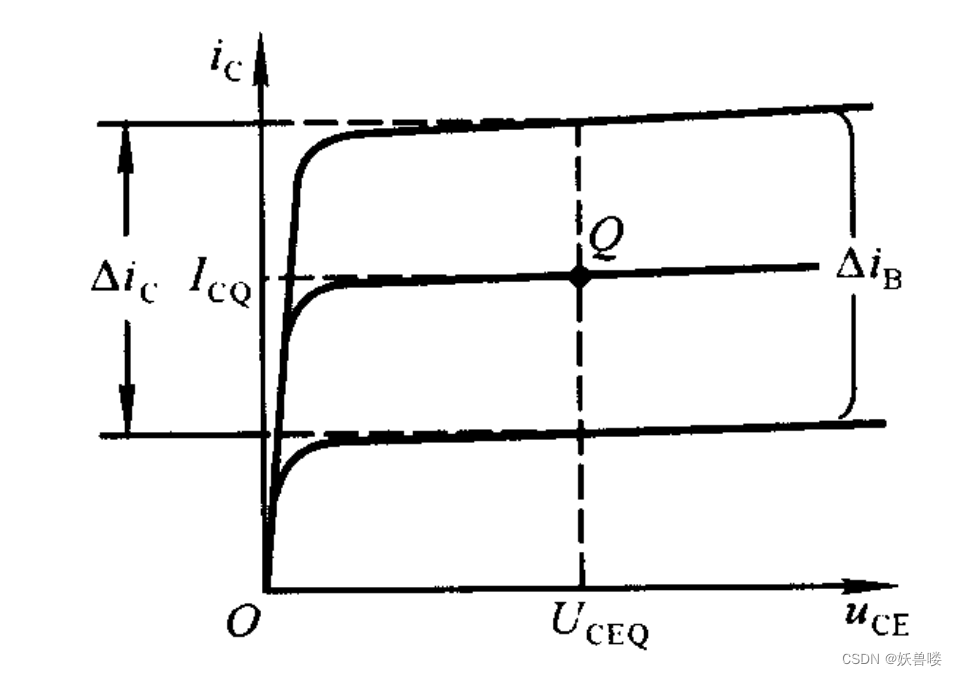
h參數的物理意義及求解方法——求解h21e
$h參數的物理意義及求解方法——求解{h\tiny 21e}$

?? ${h\tiny 22e}$ 是當 ${i\tiny B}={I\tiny BQ}$ 時， ${i\tiny C}$ 對 ${\large u}{\tiny CE}$ 的偏導數。從輸出特性上看， ${h\tiny 22e}$ 是在 ${\large i}{\tiny B}={I\tiny BQ}$ 的那條輸出特性曲線上Q點處導數，見下圖所示，它表示輸出特性曲線上翹的程度，可以利用 $\frac{\large \Delta i\tiny C}{\large \Delta u\tiny CE}$ 得到其近似值。由于大多數管子工作在放大區時曲線均幾乎平行于橫軸，所以其值常小于 $10^{-5}S$ 。常稱 $\frac{-1}{h\tiny 22e}$ 為 c - e 間動態電阻 ${r\tiny ce}$ ，其值在幾百千歐以上。
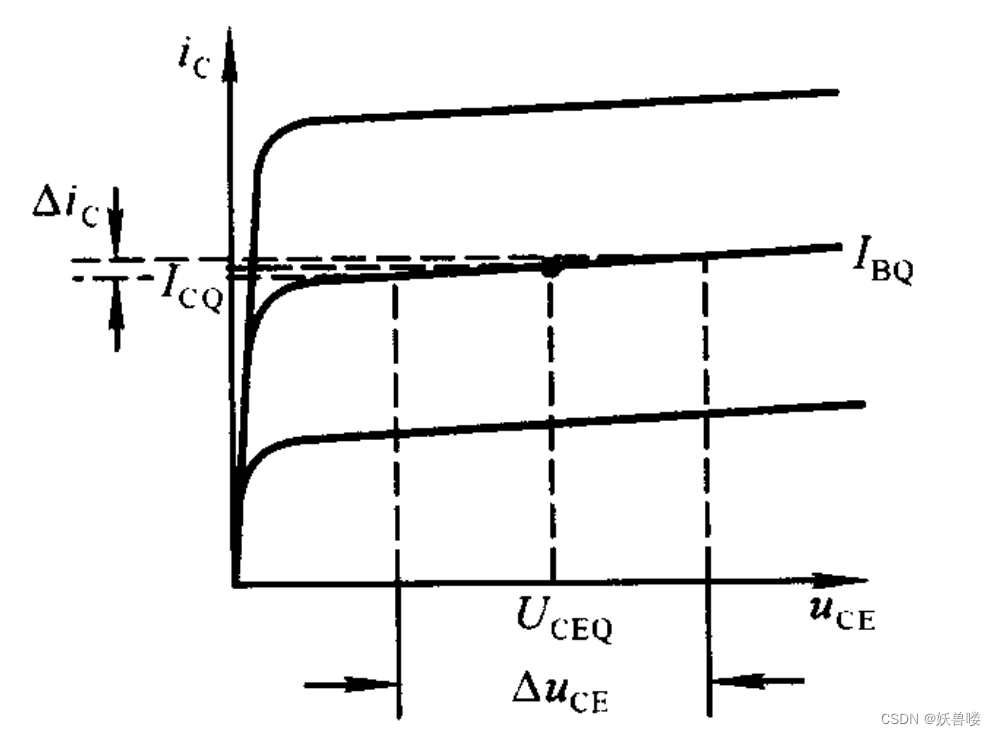
h參數的物理意義及求解方法——求解h22e
$h參數的物理意義及求解方法——求解{h\tiny 22e}$

簡化的h參數等效模型

??由以上分析可知，在輸入回路，內反饋系數 ${h\tiny 12e}$ 很小，即內反饋很弱，近似分析中可忽略不計，故晶體管的輸入回路可近似等效為只有一個動態電阻 ${r\tiny be}({h\tiny 12e})$ ；在輸出回路， ${h\tiny 22e}$ 很小，即 ${r\tiny ce}$ 很大，說明在近似分析中該支路的電流可忽略不計，故晶體管的輸出回路可近似等效為只有一個受控電流源 ${\.{I}}{\tiny c}$ ， ${\.{I}}{\tiny c}={\beta \.{I}{\tiny b}}$ ；因此，簡化的 $h$ 參數等效模型下圖所示。
??應當指出，如果晶體管輸出回路所接負載電阻 ${R\tiny L}$ 與 ${r\tiny ce}$ 可比，則在電路分析中應當考慮 $r\tiny ce$ 的影響
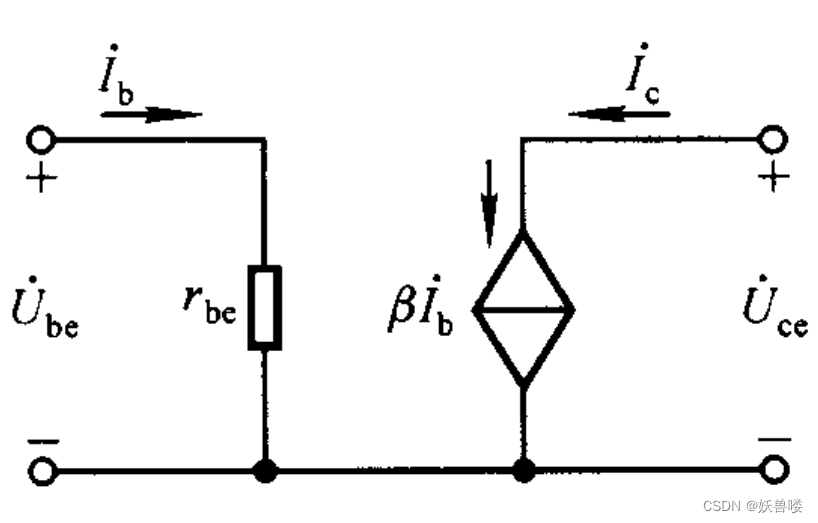
簡化的h參數等效模型
$簡化的 h 參數等效模型$

${r\tiny be}$ 的近似表達式

??在簡化的 $h$ 參數等效模型中，可以通過實測得到工作在Q點下的 $\beta$ ，并可以通過以下分析所得的近似表達式來計算 ${r\tiny be}$ 的數值。

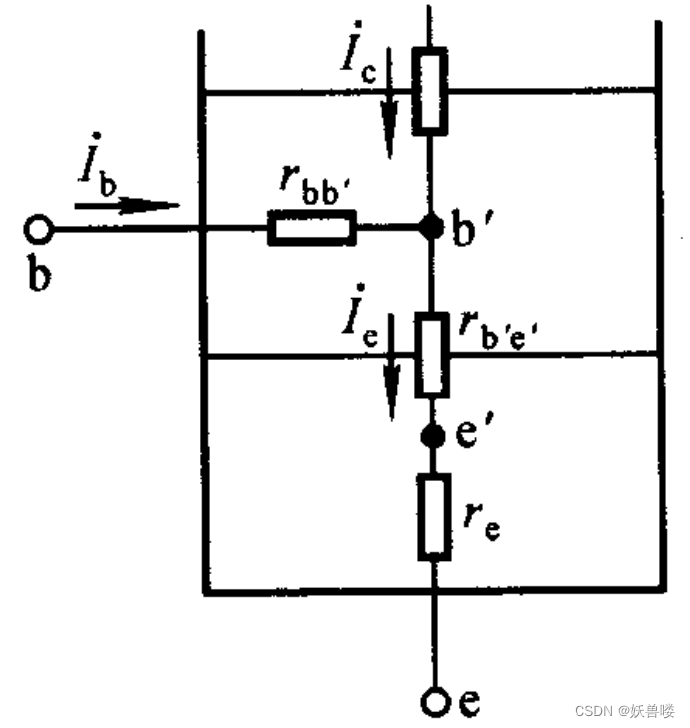
$晶體管輸入回路的分析結構$
??從上圖所示晶體管的結構示意圖中可以看出，b - e 間電阻由基區體電阻 ${\large r\tiny bb'}$ 、發射結電阻 ${\large r\tiny b'e}$ 和發射區體電阻 ${\large r\tiny e}$ 三部分組成。 ${\large r\tiny bb'}$ 與 ${\large r\tiny e}$ 僅與雜質濃度及制造工藝有關，由于基區很薄且多子濃度很低， ${\large r\tiny bb'}$ 數值較大，對于小功率管，多在幾十歐到幾百歐，可以通過查閱手冊得到。由于發射區多數載流子濃度很高， ${\large r\tiny e}$ 數值很小，只有幾歐，與 ${\large r\tiny bb'}$ 和 ${\large r\tiny b'e}$ 相比可以忽略不計。因此，晶體管輸入回路的等效電路如下圖所示。

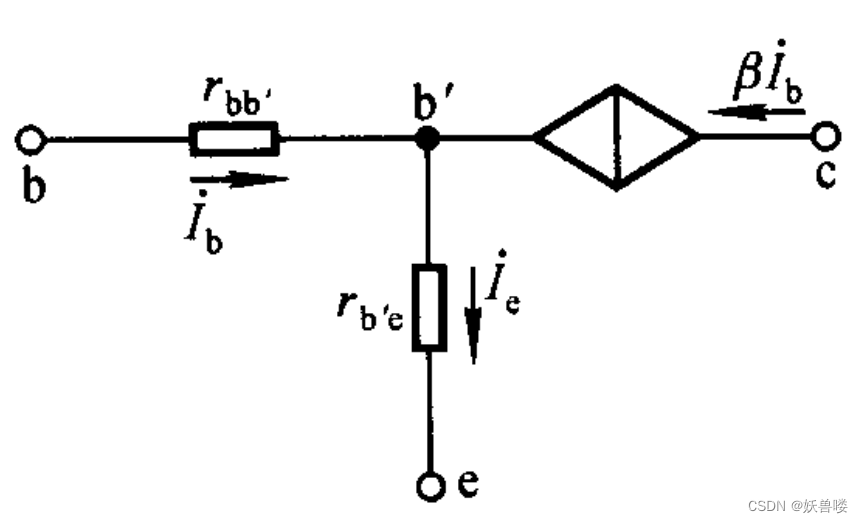
$晶體管輸入回路的分析等效電路$
流過 ${\large r\tiny bb'}$ 的電流為 ${\.{I}{\tiny b}}$ ，而流過 ${\large r\tiny b'e}$ 的電流為 ${\.{I}{\tiny e}}$ ，所以
${\.{U}{\tiny be}}≈{\.{I}{\tiny b}}{\large r\tiny bb'}+{\.{I}{\tiny e}}{\large r\tiny b'e}$
??根據對PN結電流方程的分析可知，發射結的總電流為：
${i\tiny E}={I\tiny S}({\small e}^{\frac {\small u}{\small U\tiny T}}-1)（u為發射結所加總電壓）$
因而
$\frac{1}{\large r\tiny b'e}=\frac{di\tiny E}{d\tiny u}=\frac{1}{U\tiny T}*{I\tiny S}*{{\small e}^{\frac {\small u}{\small U\tiny T}}}$
由于發射結處于正向偏置，u大于開啟電壓 (如硅管 $U\tiny on$ 為0.5 V左右)，而常溫下 ${U\tiny T}≈26mV$ ，因此可以認為 ${i\tiny E}≈{I\tiny S} *{{\small e}^{\frac {\small u}{\small U\tiny T}}}$ ，代入上式可得
$\frac{1}{\large r\tiny b'e}≈\frac{1}{U\tiny T}*{i\tiny E}$
??當用以Q點為切點的切線取代Q點附近的曲線時
$\frac{1}{\large r\tiny b'e}≈\frac{1}{U\tiny T}*{I\tiny EQ}$
??根據 $r\tiny be$ 的定義
${\large r\tiny be}=\frac{U\tiny be}{I\tiny b}≈\frac{{U\tiny bb'}+{U\tiny b'e}}{I\tiny b}=\frac{U\tiny bb'}{I\tiny b}+\frac{U\tiny b'e}{I\tiny b}={\large r\tiny bb'}+\frac{{I\tiny e}\large r\tiny b'e}{I\tiny b}$
由此得出 $\large r\tiny be$ 的近似表達式
${\large r\tiny be}≈{\large r\tiny bb'}+(1+{\beta})\frac{U\tiny T}{I\tiny EQ}或{\large r\tiny be}≈{\large r\tiny bb'}+{\beta}\frac{U\tiny T}{I\tiny CQ}$
上進一步表明，Q點越高，即 ${I\tiny EQ}({I\tiny CQ})$ 越大， ${\large r\tiny be}$ 越小。
?? $h$ 參數等效模型用于研究動態參數，它的四個參數都是在Q點處求偏導數得到的。因此，只有在信號比較小，且工作在線性度比較好的區域內，分析計算的結果誤差才較小。而且，由于 $h$ 參數等效模型沒有考慮結電容的作用，只適用低頻信號的情況，故也稱之為晶體管的低頻小信號模型。

共射放大電路動態參數的分析

$（ a ）基本共射放大電路$
??利用 $h$ 參數等效模型可以求解放大電路的電壓放大倍數、輸人電阻和輸出電阻。在放大電路的交流通路中，用h參數等效模型取代晶體管便可得到放大電路的交流等效電路。上圖所示基本共射放大電路的交流等效電路下圖所示。

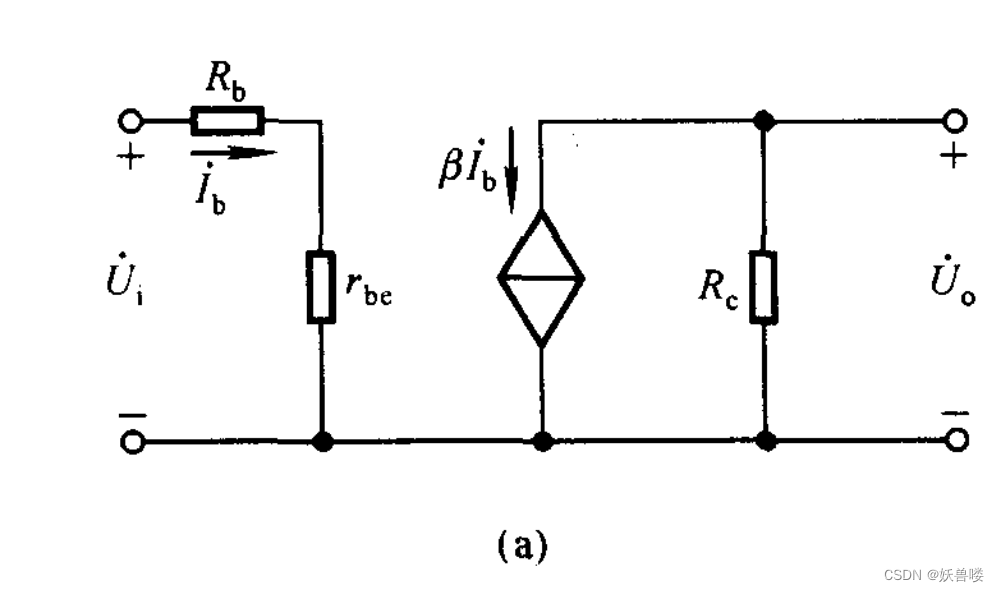
$基本共射放大電路的動態分析交流等效電路$

電壓放大倍數 $\.{A}\tiny u$

??根據電壓放大倍數的定義，利用晶體管 ${\.{I}}{\tiny b}$ 對 ${\.{I}}{\tiny c}$ 的控制關系，可得 ${\.{U}\tiny i}={\.{I}\tiny b}({R\tiny b}+{\large r}{\tiny be})$ ， ${\.{U}\tiny o}=-{\.{I}\tiny c}{R\tiny c}=-{\beta}{\.{I}\tiny b}{\large R}{\tiny c}$ 因此電壓放大倍數的表達式為:
${\.{A}\tiny u}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=\frac{\beta R\tiny c}{{R\tiny b}+{\large r}{\tiny be}}$

輸入電阻 ${R\tiny i}$

?? ${R\tiny i}$ 是從放大電路輸入端看進去的等效電阻。因為輸入電流有效值 ${I\tiny i}={I\tiny b}$ ，輸入電壓有效值 ${U\tiny i}={I\tiny b}({R\tiny b}+{\large r}{\tiny be})$ ，故輸入電阻為:
${R\tiny i}=\frac{U\tiny i}{I\tiny i}={R\tiny b}+{\large r}{\tiny be}$

輸出電阻 ${R\tiny o}$

??根據諾頓定理將放大電路輸出回路進行等效變換，使之成為一個有內阻的電壓源，如下圖基本共射放大電路的動態分析輸出電阻的分析所示，可得
${R\tiny o}={R\tiny c}$

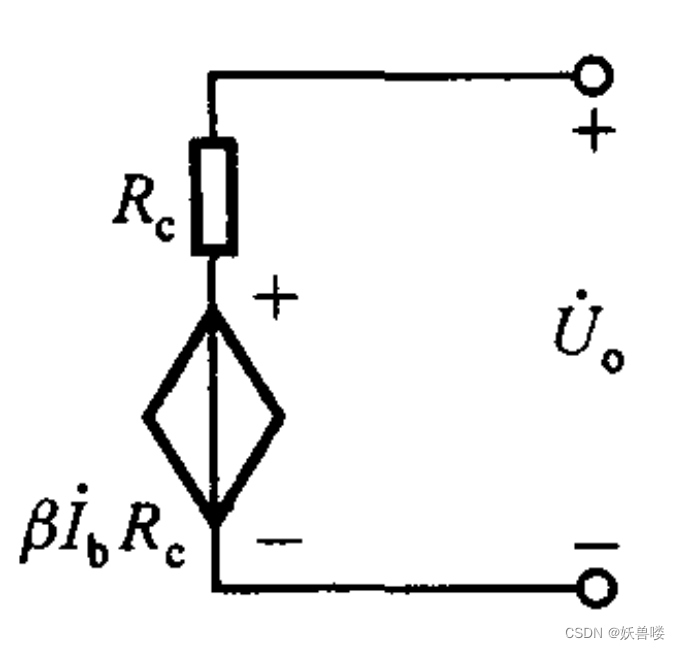
$基本共射放大電路的動態分析輸出電阻的分析$
??對電子電路輸出電阻進行分析時，還可令信號源電壓 ${\.{U}\tiny S}=0$ ，但保留內阻 ${R\tiny s}$ ；然后，在輸出端加一正弦波測試信號 ${U\tiny o}$ ，必然產生動態電流 ${I\tiny o}$ ，則
${R\tiny o}=\frac{U\tiny o}{I\tiny o}{\huge \mid_{\small U{\tiny s}=0}}$
??在基本共射放大電路的動態分析交流等效電路所示電路中，所加信號 ${\.{U}\tiny i}$ 為恒壓源，內阻為0。當 ${\.{U}\tiny i}=0$ 時， ${\.{I}\tiny b}=0$ ，當然 ${\.{I}\tiny c}=0$ ，因此，
${R\tiny o}=\frac{U\tiny o}{I\tiny o}=\frac{U\tiny o}{{U\tiny o}{R\tiny c}}={R\tiny c}$
??應當指出，雖然利用 $h$ 參數等效模型分析的是動態參數，但是由于 ${\large r}{\tiny be}$ 與Q點緊密相關，因而使動態參數與Q點緊密相關;對放大電路的分析應遵循“先靜態，后動態”的原則，只有Q點合適，動態分析才有意義。
??上述分析方法為等效電路法，有些文獻也稱之為微變等效電路法。

??在下圖所示電路中，已知 ${V\tiny BB}=1 V$ ， $R{\tiny b}= 24 kΩ$ ， ${V\tiny CC}=12V$ ， $R{\tiny c}= 5.1 kQ$ ；晶體管的 ${\large r}{\tiny bb'}=100Ω$ ， ${\beta}=100$ ，導通時的 $U\tiny BEQ$ =0.7 V。
??(1)求靜態工作點Q;
??(2)求解 $\.{A}\tiny u$ 、 ${R\tiny b}$ 和 ${R\tiny o}$ 。

$（ a ）基本共射放大電路$
解:
(1）根據
$\begin{cases} {I\tiny BQ}=\frac{{V\tiny BB}-{U\tiny BEQ}}{R\tiny b} \\ {I\tiny CQ}={\={\beta}}{I\tiny BQ}={\beta}{I\tiny BQ} \\ {U\tiny CEQ}={V\tiny CC}-{I\tiny CQ}{R\tiny c} \end{cases}$
求出Q點
${I\tiny BQ}=\frac{{V\tiny BB}-U{\tiny BEQ}}{R\tiny b}=\frac{{1-0.7}}{24*10^{3}}A=({12.5*10^{-6}})A=12.5uA$
${I\tiny CQ}={\={\beta}}{I\tiny BQ}={\beta}{I\tiny BQ}=(100*12.5*10^{-6})A=1.25mA$
${U\tiny CEQ}={V\tiny CC}-{I\tiny CQ}{R\tiny c}=(12-1.25*5.1)V≈5.63V$
$U\tiny CEQ$ 大于 $U\tiny BEQ$ ，說明晶體管工作在放大區。
(2）動態分析時，先求出 ${r\tiny be}$ 。
${\large r\tiny be}≈{\large r\tiny bb'}+{\beta}\frac{U\tiny T}{I\tiny CQ}=(100+100\frac{26}{1.25})Ω≈2200Ω=2.2kΩ$
根據
${\.{A}\tiny u}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=\frac{\beta R\tiny c}{{R\tiny b}+{\large r}{\tiny be}}$ ${R\tiny i}=\frac{U\tiny i}{I\tiny i}={R\tiny b}+{\large r}{\tiny be}$ ${R\tiny o}={R\tiny c}$
可得
${\.{A}\tiny u}=-\frac{\beta R\tiny c}{{R\tiny b}+{\large r}{\tiny be}}≈-\frac{100*5.1}{24+2.2}≈-19.5$
${R\tiny i}={R\tiny b}+{\large r}{\tiny be}≈(24+2.2)kΩ=26.2kΩ$
${R\tiny o}={R\tiny c}=5.1kΩ$

【例2.3.3】在下圖阻容耦合共射放大電路所示電路中，已知 ${V\tiny CC}=12V$ ， $R{\tiny b}= 510 kΩ$ ， ${R\tiny c}=3kΩ$ ;晶體管的 ${\large r\tiny bb'}= 150Ω$ ， $\beta =80$ ， ${U\tiny BEQ}=0.7V$ ; ${R\tiny L}=3kΩ$ ;耦合電容對交流信號可視為短路。
(1）求出電路的 $\.{A}\tiny u$ 、 ${R\tiny b}$ 和 ${R\tiny o}$ 。
(2)若所加信號源內阻 $R{\tiny s}= 2 kΩ$ ，求出 $\.{A}{\tiny us}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny s}}=?$

$（ c ）阻容耦合共射放大電路$
解:
(1）首先求出Q點和 ${r\tiny be}$ ，再求出 $\.{A}\tiny u$ 、 ${R\tiny b}$ 和 ${R\tiny o}$ 。
根據
$\begin{cases} {I\tiny BQ}=\frac{{V\tiny CC}-{U\tiny BEQ}}{R\tiny b}\\ {I\tiny CQ}={\={\beta}}{I\tiny BQ}={\beta}{I\tiny BQ} \\ {U\tiny CEQ}={V\tiny CC}-{I\tiny CQ}{R\tiny c} \end{cases}$
可得
${I\tiny BQ}=\frac{{V\tiny CC}-U{\tiny BEQ}}{R\tiny b}=\frac{{12-0.7}}{510}mA≈(0.0222)mA=22.2uA$
${I\tiny CQ}={\beta}{I\tiny BQ}=(80*0.0222)mA≈1.77mA$
${U\tiny CEQ}={V\tiny CC}-{I\tiny CQ}{R\tiny c}≈(12-1.77*3)V=6.69V$
$U\tiny CEQ$ 大于 $U\tiny BEQ$ ，說明Q點晶體管工作在放大區。
${\large r\tiny be}≈{\large r\tiny bb'}+{\beta}\frac{U\tiny T}{I\tiny CQ}=(150+80\frac{26}{1.77})Ω≈1325Ω=1.33kΩ$
畫出交流等效電路，如下圖所示。
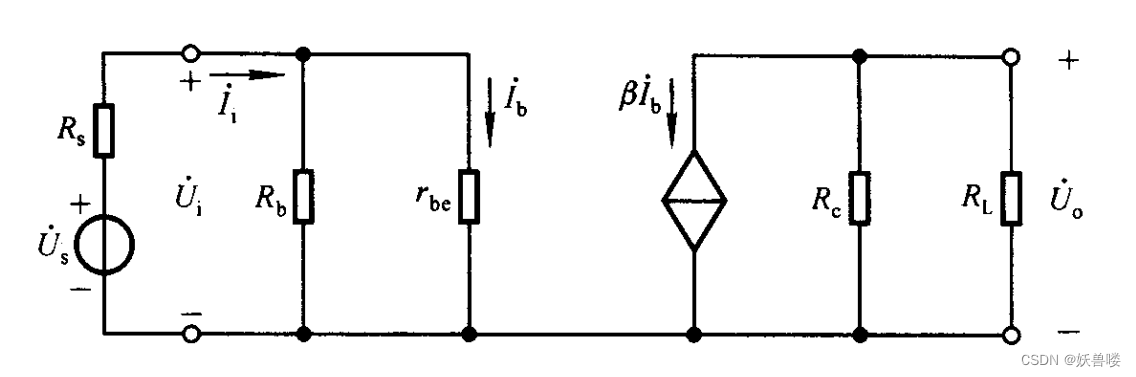
在這里插入圖片描述

從圖上圖可知， ${\.{U}{\tiny o}}={\.{I}{\tiny c}}({R\tiny c}//{R\tiny L})=-\beta{\.{I}{\tiny b}}({R\tiny c}//{R\tiny L})$ ， ${\.{U}{\tiny i}}={\.{I}{\tiny b}}{\large r\tiny be}$ ，根據 $\.{A}\tiny u$ 的定義可以得出
${\.{A}\tiny u}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=-\frac{\beta R'\tiny L}{{\large r}{\tiny be}}（{ R'\tiny L}={R\tiny c}//{R\tiny L}）$
帶入數據
${\.{A}\tiny u}=-80*\frac{\frac{3*3}{3+3}}{1.33}≈-90$
根據 $R\tiny i$ 定義可以得出
${R\tiny i}=\frac{U\tiny i}{I\tiny i}={R\tiny b}//{\large r}{\tiny be}$
通常情況下 ${R\tiny b}>>{\large r}{\tiny be}$ ，所以 ${R\tiny i}≈{\large r}{\tiny be}≈1.33kΩ$ 。
${R\tiny o}={R\tiny c}$
代入數據，得 ${R\tiny o}=3kΩ$ 。
應當指出，放大電路的輸入電阻與信號源內阻無關，輸出電阻與負載無關。

(2)根據 $\.{A}{\tiny us}$ 的定義
${\.{A}{\tiny us}}=\frac{\.{U}{\tiny o}}{\.{U}{\tiny s}}=\frac{\.{U}{\tiny i}}{\.{U}{\tiny s}}*\frac{\.{U}{\tiny o}}{\.{U}{\tiny i}}=\frac{R\tiny i}{{R\tiny s}+{R\tiny i}}*{\.{A}{\tiny u}}$
代入數據后，得
${\.{A}{\tiny us}}==\frac{1.33}{2+1.33}*(-90)≈-36$
$|\.{A}{\tiny us}|$ 總是小于 $|\.{A}{\tiny u}|$ ，輸入電阻越大， $|\.{U}{\tiny i}|$ 越接近 $|\.{U}{\tiny s}|$ ， $|\.{A}{\tiny u}|$ 也就越接近 $|\.{A}{\tiny us}|$