目錄

解法：

官方解答：

方法一：深度優先搜索

方法二：廣度優先搜索

思路與算法

復雜度分析

時間復雜度：

空間復雜度：

---

給定一個二叉樹?root?，返回其最大深度。

二叉樹的?最大深度?是指從根節點到最遠葉子節點的最長路徑上的節點數。

示例 1：

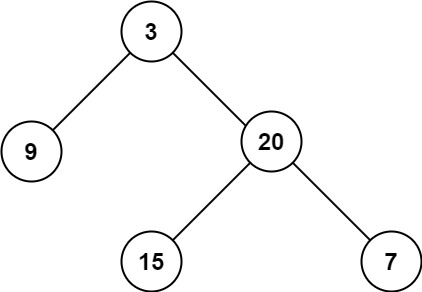
輸入：root = [3,9,20,null,null,15,7]
輸出：3

示例 2：

輸入：root = [1,null,2]
輸出：2

提示：

• 樹中節點的數量在?[0, 104]?區間內。
• -100 <= Node.val <= 100

解法：

直接使用深度優先遍歷方法遍歷到最深然后返回數字。

class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;}
}

---

官方解答：

方法一：深度優先搜索

與上面所寫思想差不多

方法二：廣度優先搜索

思路與算法

我們也可以用「廣度優先搜索」的方法來解決這道題目，但我們需要對其進行一些修改，此時我們廣度優先搜索的隊列里存放的是「當前層的所有節點」。每次拓展下一層的時候，不同于廣度優先搜索的每次只從隊列里拿出一個節點，我們需要將隊列里的所有節點都拿出來進行拓展，這樣能保證每次拓展完的時候隊列里存放的是當前層的所有節點，即我們是一層一層地進行拓展，最后我們用一個變量 ans 來維護拓展的次數，該二叉樹的最大深度即為 ans。

class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);int ans = 0;while (!queue.isEmpty()) {int size = queue.size();while (size > 0) {TreeNode node = queue.poll();if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}size--;}ans++;}return ans;}
}

復雜度分析

時間復雜度：

O(n)O，其中 n 為二叉樹的節點個數。與方法一同樣的分析，每個節點只會被訪問一次。

空間復雜度：

此方法空間的消耗取決于隊列存儲的元素數量，其在最壞情況下會達到 O(n)。

---

官方解答部分：

作者：力扣官方題解
鏈接：https://leetcode.cn/problems/maximum-depth-of-binary-tree/
來源：力扣（LeetCode）
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請注明出處。