數學,改變世界的基石。微積分十九世紀的三大自然發現之一,迪卡爾建立了解析幾何,把數與圖結合在一起,微積分的發現與創立,是數學新的里程碑,解決了常規方法無法解決的問題,是一次偉大的革命。迪卡爾的解析幾何,牛頓的微積分,都是創造,互相關聯,缺一不可。
前言
數學,改變世界的基石。偉大的數學家有牛頓、阿基米德、萊布尼茨、歐拉、拉格朗日、拉普拉斯、高斯、約翰·伯努利、龐加萊、黎曼、歐幾里得、克萊因、笛卡爾、狄利克雷、費馬、畢達哥拉斯、洛必達等。
阿基米德、牛頓、高斯是站在金字塔頂端的人物,是數學史上的天才,再加上一個歐拉,這四人是數學史上公認的4名最偉大的數學家。
數學其實挺美,并不枯燥。你覺得枯燥只是因為你被灌輸的知識,習慣了死背公式,沒搞懂原理并把它用起來。拿微積分舉例,看下它的起源和強大的用途。
微積分十九世紀的三大自然發現之一,迪卡爾建立了解析幾何,把數與圖結合在一起,微積分的發現與創立,是數學新的里程碑,解決了常規方法無法解決的問題,是一次偉大的革命。迪卡爾的解析幾何,牛頓的微積分,都是創造,互相關聯著,缺一不可。
微積分是數學中的一門重要分支,涉及到函數、極限、導數、積分、微分方程等多個概念,在工程、科學、經濟等領域都有廣泛的應用。微積分分為五個主要的章節:導數與微分、積分與定積分、微分方程與應用、多元函數與偏導數、向量函數與曲線積分。
真正理解了“微積分的基本定理”,就會覺得這東西并不復雜。但是,這個定理的厲害之處在于應用范圍很廣。雖然看起來很普通,但是很實用。可惜大學的課程往往只講公式,不講原理,聽的人云里霧里的。
以下拿一個真實的應用,來分析下什么是微積分。微積分不是一個獨立的詞,它包含了微分和積分。
先從積分開始
先來了解下積分,為何先從積分開始?
阿基米德在公元前 3 世紀就研究了用于計算面積的積分,牛頓和萊布尼茨在 17 世紀才想出微分的方法。二者中間相差了1800年以上的時間。
幾乎所有的大學數學教科書都先說明微分后再引入其逆運算—不定積分。而且,用于計算面積的定積分被定義為不定積分的差。雖然按照上述順序有邏輯地教授數學當然合乎情理,但歷史上的發展順序恰好相反。阿基米德在公元前?3?世紀就研究了用于計算面積的積分,牛頓和萊布尼茨在 17 世紀才想出微分的方法。二者中間相差了1800年以上的時間。
在歷史上積分先被發現,這其中存在一定原因。積分與面積、體積等具體量的計算有著直接的關系。另外,研究微分前,首先必須準確地理解無窮小和極限等概念。例如物體運動的速度需要通過微分定義,不過因為在古希臘時期并沒有確定極限的概念,所以出現了芝諾的“飛矢不動”悖論。
因此在學習復雜的微分前,最好還是正確把握從直覺上相對容易理解的積分,再來思考其逆運算微分。因此,先解釋積分。不管你是在大學的微積分課上聽得不明不白,還是正在打算開始學習微積分,都可以試著“先從積分開始”。
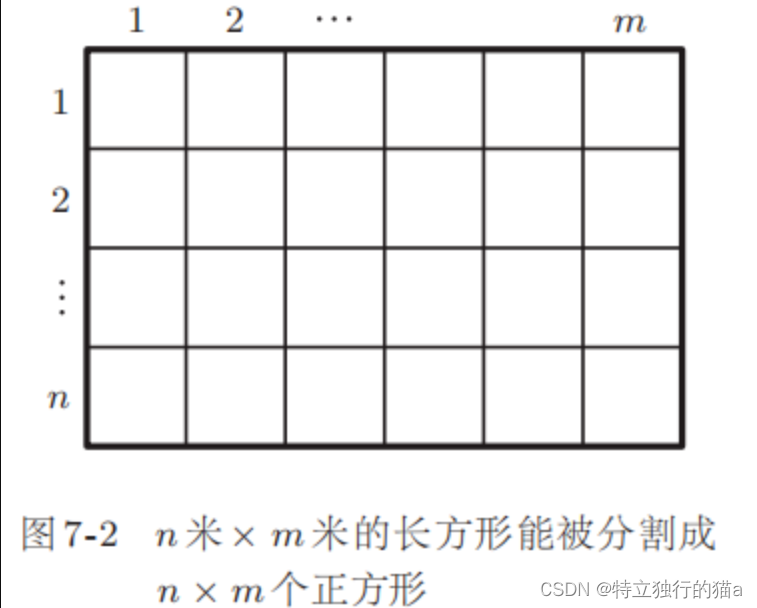
積分是從計算圖形面積開始的。面積的單位包括平方米、平方千米等,即都帶有“平方”二字。邊長為1米的正方形面積等于1平方米。也就是說,面積是以正方形作為單位,計算圖形的面積相當于幾個正方形。如果是長方形,該如何計算面積呢?在小學階段,我們就學過長方形的面積是長和寬的乘積,不過現在我們先假裝不知道長方形面積如何計算的,只知道正方形的面積計算,沒有學過長方形這個計算公式。
假設已知長方形寬 1 米,長 2 米,那么豎著從正中間將長方形分成兩個部分,就得到兩個邊長為 1 米的正方形,所以長方形的面積就等于 2 平方米。也就是說,長和寬的乘積等于長方形的面積。
接下來再假設 n 和 m 均為自然數,已知長方形寬 n 米,長 m 米,那么只要寬被等分成 n 部分,長度被等分成 m 部分,就能得到 n × m個邊長為 1 米的正方形(圖 7-2)。該長方形的面積正好等于正方形面積的 n × m 倍,即 n × m 平方米。結果還是等于長和寬的乘積。
積分究竟計算什么
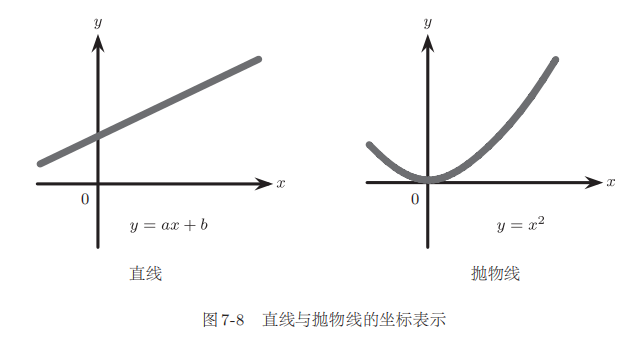
使用阿基米德的夾逼定理,能計算更復雜的曲線圖形的面積。用笛卡兒坐標表示的話,如圖?78?所示,直線可以表示為?y?=?ax?+?b,拋物線表示為
![]()
假設已知某函數?f(x),那么我們來思考一下曲線?y?=?f(x)。如圖7-9?所 示,假 設 在 區 間?a?≤?x?≤?b上?f(x)?的值始終大于?0,那么我們來研究一下曲線?y?=?f(x)?和y?= 0、x?=?a、x?=?b?這三條直線圍成的圖形?A(圖中的陰影部分)。如果知道如何計算圖形?A?的面積,就能通過拼組的方法計算任何曲線圍成的圖形面積。
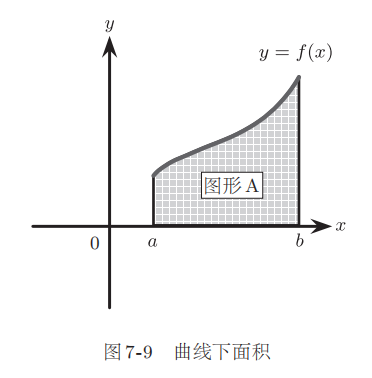
曲線?y?=?f(x)?沿著?y?軸方向上升或下降。為了便于計算,假設在區間?a?≤?x?≤?b?上,y?=?f(x)?一直在增大。在其他情況下,將區間a?≤?b?分成兩部分,即?f(x)?不斷增大的區間和?f(x)?不斷減小的區間。只要將以下方法分別代入上述兩個區間即可。
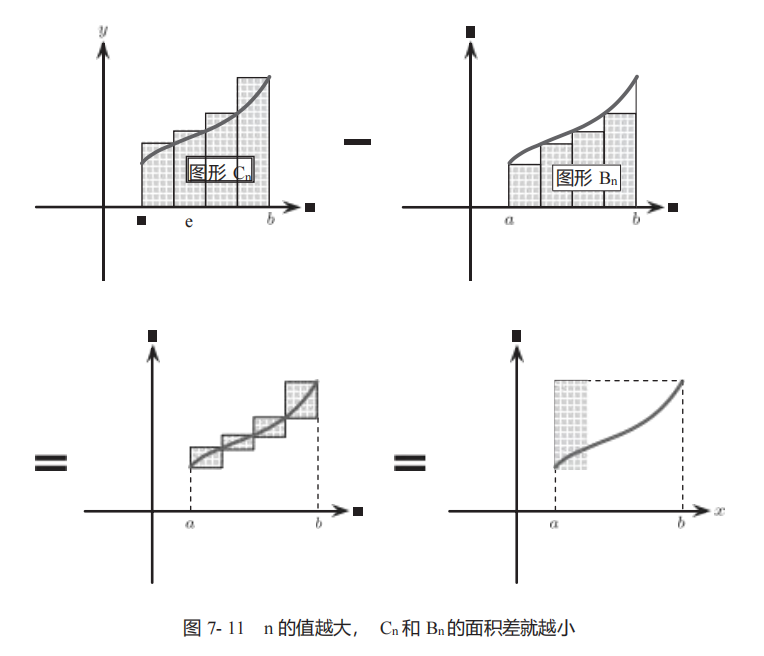
為了用阿基米德的夾逼定理來計算圖形?A?的面積,首先將區間a?≤?x?≤?b?分成?n?部分,如圖?710?中的圖形?Bn?和?Cn。圖形?A?包含圖形?Bn,同時被包含在圖形?Cn?中。圖形?Bn?和?Cn?均是長方形集合,所以能夠計算出面積。
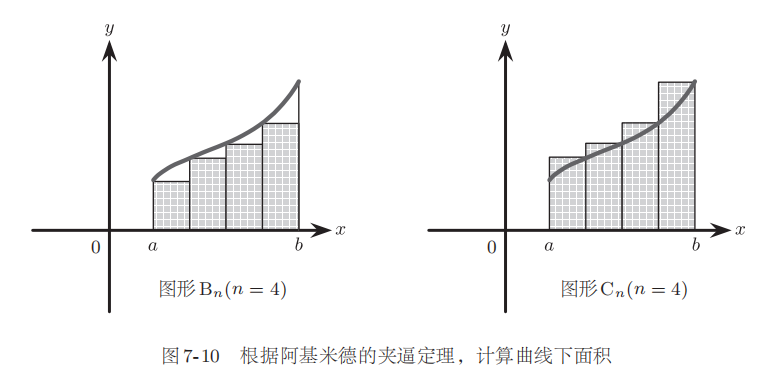
如圖?711?所示,面積?(Cn)?和面積?(Bn)?的差等于
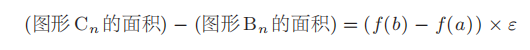
也就是底?ε?= (b???a)/n、高?= (f(b)???f(a))?的長方形的面積。n?的值越大,ε?的值就越小,因此圖形?Bn?和圖形?Cn?的面積就越接近。當?ε?的值達到極限即等于?0?時,兩個圖形的面積相等。達到極限時的值也就是圖形?A?的面積。
按照上述方法計算的圖形?A?的面積叫作“函數?f(x)?在區間?a?≤?x?≤?b上的積分”,用公式記作
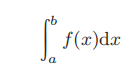
與牛頓同時創立微積分法的萊布尼茨發明了符號
![]()
是“求和”(sum)的首字母“S”的拉長。而且,“dx”的 d 是指“求差”(difference)的首字母。當將圖形近似為長方形集合時, 一個長方形的底長等于 x + ε 和
x 的“差”。高為 f(x)、底為 e 的長方形面積等于 f(x)e, 因此可以用符號 dx 代替 e,即 f(x)dx。也就是說,
![]()
中包含著萊布尼茨的想法, 即“積分是指在 x = a 到 b 的區間上排列出高等于 f(x)、底為 dx 的長方形,并求出它們的面積之和”。

上文中解釋的積分沿用了 19 世紀德國數學家波恩哈德 ·黎曼的定義,所以稱作“黎曼積分”。其實積分包括許多類,例如法國數學家亨利 ·勒貝格提出的“勒貝格積分”、日本數學家伊藤清提出的“伊藤積分”等。黎曼積分足以處理我們在高中所學的函數問題,不過當我們需要處理類似股票價格等隨機波動的數值時,則需要用到伊藤積分。伊藤積分還被用于決定期權的價格, 因此伊藤清被認為是“在華爾街最有名的日本人”。
不定積分與定積分
定積分和不定積分是微積分中兩個重要的概念。定積分可以理解為函數在某個區間內的面積,而不定積分是函數的反導數(原函數)。積分是微積分理論的另一個重要分支,它可以用來計算曲線下方的面積、弧長、體積以及質心等。
積分分為不定積分和定積分,定積分是一個數,而不定積分是一個表達式。在計算定積分時,我們需要先找到被積函數的原函數,然后進行定積分的計算。通過牛頓-萊布尼茨公式,我們可以將定積分的計算轉化為不定積分的計算。不定積分和定積分的存在性也有所不同。連續函數一定存在不定積分,而只有當函數在有限區間內只有有限個間斷點且函數有界時,才存在定積分。
總之,不定積分是微積分中的一個重要概念,它是求一個函數的原函數或反導數的過程。

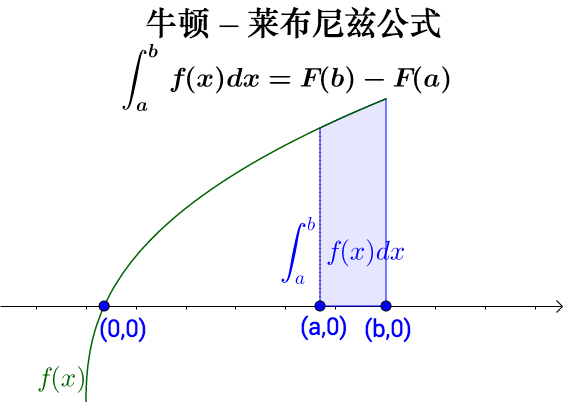
牛頓-萊布尼茨公式
牛頓-萊布尼茨公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函數的原函數或者不定積分之間的聯系。公式的內容是一個連續函數在區間 [ a,b ] 上的定積分等于它的任意一個原函數在區間[ a,b ]上的增量。
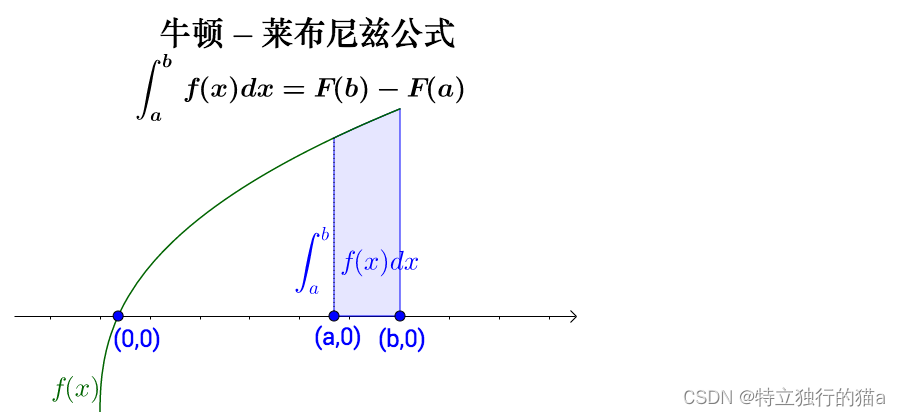
牛頓-萊布尼茨公式的發現,使人們找到了解決曲線的長度,曲線圍成的面積和曲面圍成的體積這些問題的一般方法。它簡化了定積分的計算,只要知道被積函數的原函數,總可以求出定積分的精確值或一定精度的近似值。
牛頓-萊布尼茨公式是聯系微分學與積分學的橋梁,它是微積分中最基本的公式之一。它證明了微分與積分互為逆運算,同時在理論上標志著微積分完整體系的形成,從此微積分成為一門真正的學科。
牛頓-萊布尼茨公式簡化了定積分的計算,利用該公式可以計算曲線的弧長,平面曲線圍成的面積以及空間曲面圍成的立體體積,這在實際問題中有廣泛的應用,例如計算壩體的填筑方量。
牛頓-萊布尼茨公式在物理學上也有廣泛的應用,計算運動物體的路程,計算變力沿直線所做的功以及物體之間的萬有引力。
牛頓-萊布尼茨公式促進了其他數學分支的發展,該公式在微分方程,傅里葉變換,概率論,復變函數等數學分支中都有體現。
牛頓 - 萊布尼茨公式提供了計算定積分的簡便的基本方法,即求定積分的值,只要求出被積函數f(x)的一個原函數F(x),然后計算原函數在區間[a,b]上的增量F(B)-F(a)即可。該公式把計算定積分歸結為求原函數的問題,揭示了定積分與不定積分之間的內在聯系。
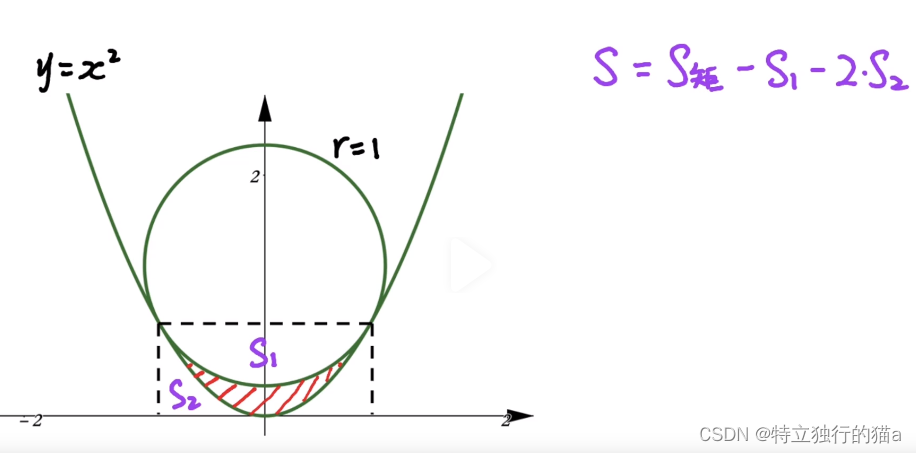
舉例,如何求解以下紅色區域的陰影面積?S = S矩-S1-2S2,類似求解陰影面積的題,學生時代的你是否覺得很恐怖?心想不如先求下我的心里陰影面積。
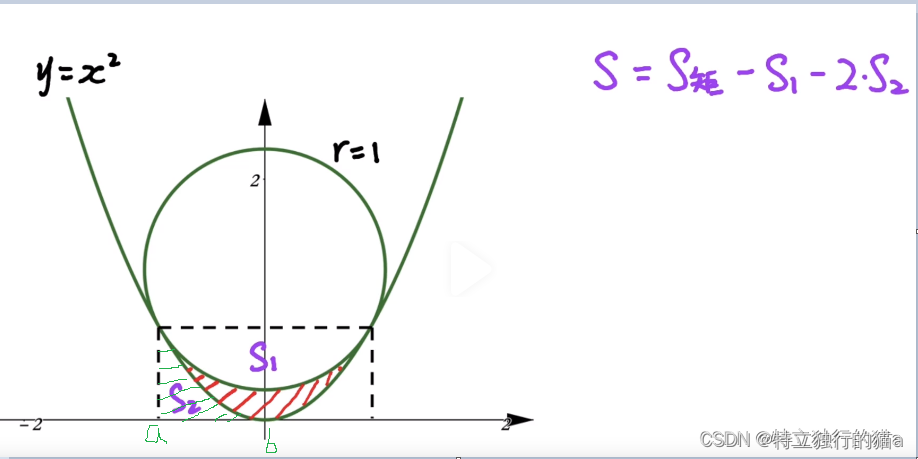
S2的綠色陰影面積如何求得?可以借助積分,從a點到b點的積分,
可以寫作:
![]()
其中包含著萊布尼茨的想法, 即“積分是指在 x = a 到 b 的區間上排列出高等于 f(x)、底為 dx 的長方形,并求出它們的面積之和”。
那么接下來呢?表示是表示出來了,如何計算從a到b的綠色陰影的面積?即定積分如何計算?
用定義來計算定積分一般是很困難的,下面將要介紹的牛頓一萊布尼茨公式不僅為定積分的計算提供了一個有效的方法,而且在理論上把定積分與不定積分聯系了起來。

F(x)叫做f(x)的原函數,f(x)叫做F(x)的導數。
根據牛頓-萊布尼茲公式,求積分變得簡單了,變成了一>求原函數。
計算由拋物線y=x^2和x軸(假設從0到1),所圍成的曲邊梯形的面積A:

F(b) - F(a), 就等于1/3 - 0? =? 1/3。因此所圍成的那一部分曲線面積為1/3。?
因此上上圖中的s2部分的綠色陰影面積可以利用微積分求解出來。s2 = (1/3)*b^3 - (1/3)*a^3
上述的f(x) = x^2是一條拋物線,如果換成是一條直線就更容易看出來了。如果f(x) = x,則可以看做是一條從0坐標開始的勻速運動:

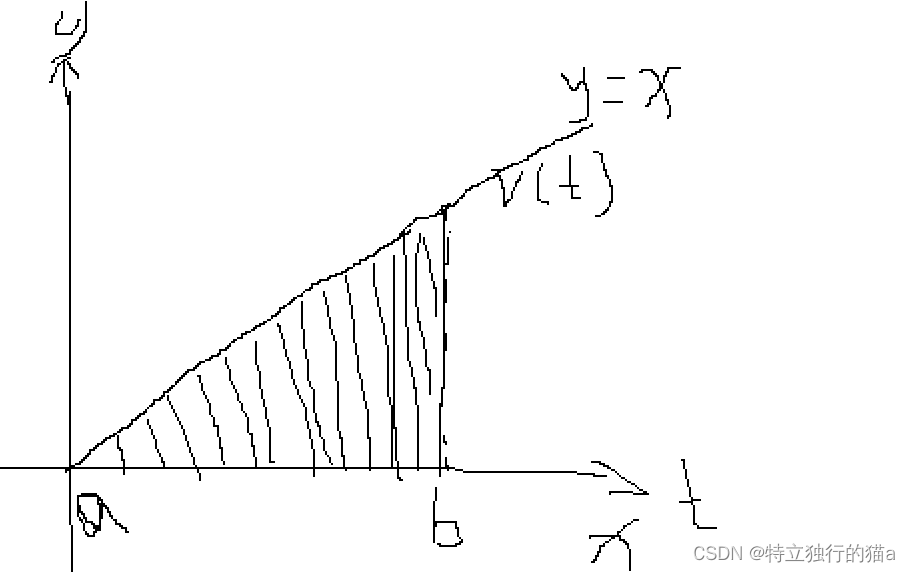
?設a=0,b=2 ,則圖上三角形的面積 = 底*高/2 ,等于2*2/2 = 2。如果用積分算一算:
S(b) = x^2/2 = 2, S(a) = 0, S(b) - S(a) = 2。會發現使用三角形面積公式和使用積分算出來是一致。
計算示例
以下再給出幾個就定積分的例子,方便理解。

函數y=sinx的反函數叫做反正弦函數,記作x=arcsiny,習慣上用x表示自變量,用y表示函數,所以反正弦函數寫成y=arcsinx,定義域是 [-1,1] ,值域是y∈ [-π/2 , π/2]?; 如果x = sin t,則t = arcsin x。其中arcsin x是反正弦函數,表示對于給定的x值,對應的sin t值。arcsin 1 的值為 π/2。在三角函數中, arcsin x 表示對于給定的 x 值,對應的 sin t 值。在這個例子中,x 的值為 1, 對應的 sin t 值為 sin(π/2) = 1。

ln是對數運算符,e是指數運算符,它們的關系和加減、乘除的關系一樣,表示相逆的兩種運算。若y=lnx,則x=e^y(e的y次方)。?e^x和ln(x)分別是自然指數函數和自然對數函數,是一對函數與反函數,e是自然常數,約等于2.718182
e與In的轉化公式,公式如下:e^ln(x)=x,ln(e^x)=x,lne=1,lnx=y,x=e^y
對數函數的求導:


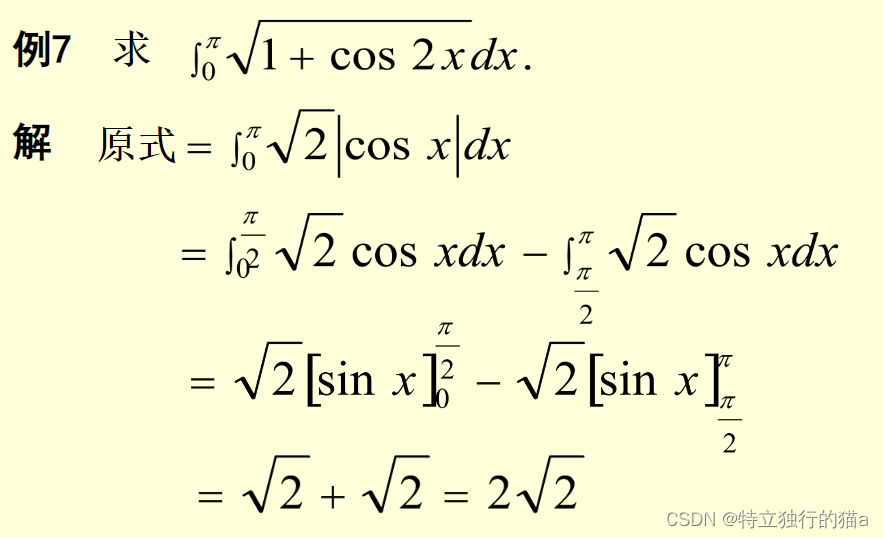


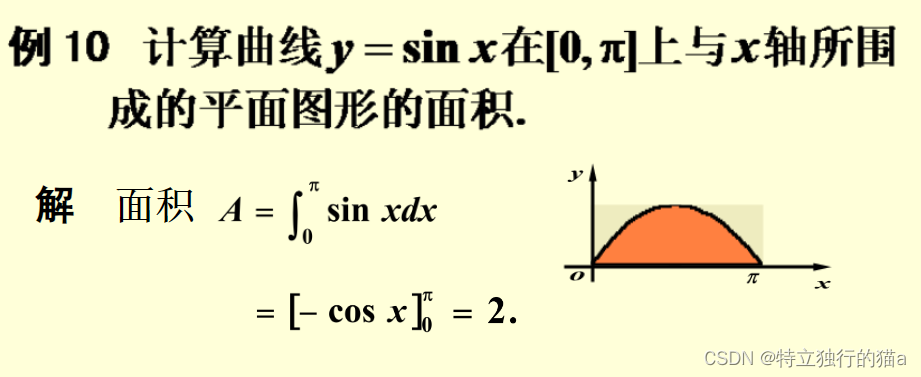
導數與微分
既然上面使用牛頓-萊布尼茲公式已經表達出來了積分,為什么還要提導數和微分呢?因為上面你只是簡單的使用了公式,如何求解積分?公式是怎么來的?這就跟導數和微分有關系了。

導數描述了函數在某一點的變化率,而微分則描述了函數在整個定義域上的變化情況。導數(求切線)是微積分重要的組成部分,在此基礎上,數學家由研究了它的反運算(積分),完成了面積的求解。
通過研究函數的導數和微分,我們可以獲得更多關于函數性質的信息,從而更好地理解和分析函數的行為。 此外,導數和微分也在數值計算中發揮著重要作用。通過計算函數的導數,我們可以確定函數的極值點、拐點和切線方程等信息。微分方程則是研究自然界中許多現象的重要工具。
導數和微分是微積分理論的基礎,它們可以用來描述曲線的變化率、切線斜率以及局部增長和減少的趨勢等。導數是函數在某一點的變化率,用極限的概念表示;微分是函數在某一點的切線的近似值,用微分算子的形式表示。導數和微分是密切相關的,在求解導數的同時,也可以求出函數在某一點的微分值。
以函數 f(x) = x^2 為例,其導數的計算公式為:

在微積分中,由于極限的存在性,我們可以通過逐步縮小?△x 的值,從而求得 f(x) 在某一點的導數值。此外,微分也是導數的一種幾何意義,它表示函數在某一點的切線斜率,是函數在某一點處的變化率。微分的計算可以使用基本微分公式。
基本微分公式是微積分中最基礎的公式之一,它可以用來計算各種函數的微分。基本微分公式包括常數微分公式、冪函數微分公式、指數函數微分公式、對數函數微分公式、三角函數微分公式等。
常數微分公式是指對于任意常數c,其微分為0。冪函數微分公式是指對于任意冪函數y=x^n,其微分為y'=nx^(n-1)。指數函數微分公式是指對于任意指數函數y=a^x,其微分為y'=a^xlna。對數函數微分公式是指對于任意對數函數y=loga(x),其微分為y'=1/(xlna)。三角函數微分公式是指對于任意三角函數y=sin(x)、y=cos(x)、y=tan(x),其微分分別為y'=cos(x)、y'=-sin(x)、y'=sec^2(x)。
基本微分公式的應用非常廣泛,它可以用來求解各種函數的導數,從而幫助我們更好地理解函數的變化規律。在實際應用中,微分還可以用來求解曲線的切線、極值、凹凸性等問題,因此掌握基本微分公式對于學習微積分和解決實際問題都非常重要。
微積分的歷史
這首先歸功于笛卡爾創立的解析幾何,它是代數與幾何相結合的產物,使變量之間關系的定量表述成為可能,從而為微積分的創立搭起了舞臺。
牛頓(1643 - 1727),偉大的物理學家、數學家、天文學家、自然哲學家和煉金術士。在2005年更是力壓愛因斯坦,被評為“科學史上最有影響力的人”。牛頓生于英格蘭一個農民家庭,是早產兒,生后勉強存活。童年時的牛頓不是神童,成績并不突出,但喜愛讀書與制作玩具。17歲時,還在讀中學的牛頓被母親召回田莊務農,但在牛頓的舅父和中學校長的竭力勸說下,牛頓在務農9個月后又被母親允許返校學習。這位校長對牛頓母親的勸說辭中,有一句話可以說是科學史上最幸運的預言,他對牛頓的母親說:“在繁雜的農務中埋沒這樣一位天才,對世界來說將是多么巨大的損失!”
1661年,牛頓考入劍橋大學三一學院,受教于巴羅,他在大學時鉆研伽利略、開普勒、笛卡爾和沃利斯等人的著作。就數學思想的形成而言,笛卡爾的《幾何學》和沃利斯的《無窮算術》對他影響最深,正是這兩部著作引導牛頓走上了創立微積分之路。
牛頓是一個天才,這一點也是無可否認的。
1665年,牛頓22歲,他當時剛獲得了學位,大學因為倫敦大瘟疫關閉,牛頓不得不回家。在家的十八個月中,他提出了二項式定理,后來發展成一套新的數學理論,就是高等數學中的微積分。在此期間,他還研究了光學和萬有引力定律。

牛頓在1665-1966年間發明了微分(求導)和積分,他稱之為“正流數術”和“反流數術”,整理成了《流數簡論》僅供同事傳閱,從命名中可以看到牛頓微積分的運動學背景。關于流數的命名,牛頓解釋道:“我把時間看作是連續的流動或增長,而其它量則隨著時間而連續增長,我從時間的流動性出發,把所有其它量的增長速度稱之為流數。”
牛頓將微積分的基本問題表述為“已知流量間的關系,求流數關系” 和“已知變量的流數間的關系的方程,求流量間的關系”。
牛頓用“導數”求解了已知位移求速度的問題,用“積分”求解了已知速度求位移的問題,并指出如何通過這種逆運算來計算面積,從而建立了微積分基本定理。
面積計算與求切線的互逆關系,以往雖然也曾被少數人在特殊場合模糊地指出(如巴羅的《幾何學講義》),但牛頓卻能以足夠的敏銳與能力將這種互逆關系明確地作為一般規律,揭示出來,并將其作為建立微積分普遍算法的基礎,正如牛頓本人在《流數簡論》中所說:一旦積分問題可解,許多問題都將迎刃而解。牛頓將他建立的統一的算法應用于求曲線切線、曲率、拐點、曲線求長、求面積與體積、求引力與引力中心等16類問題,展示了他的算法的極大的普遍性與系統性。
這樣,牛頓就將自古希臘以來求解無限小問題的各種特殊技巧統一為兩類普遍的算法——正、反流數術亦即微分(求導)與積分,并證明了二者的互逆關系,而將這兩類運算進一步統一成整體,這是他超越前人的功績,正是在這樣的意義上,我們說牛頓發明了微積分。
當時在瑞士有個著名的數學家家族——伯努利家族,約翰·伯努利向他的哥哥雅克布·伯努利提出了最速降線問題。約翰·伯努利解決完后,又向歐洲的數學家發起挑戰。
面對挑戰,牛頓很快就解決了這個問題。值得一提的是當時的歐洲有很多天才數學家,萊布尼茲、洛比達、雅克布·伯努利等人也紛紛解決了這個問題。
要說牛頓有多厲害,在麥克·哈特所著的《影響人類歷史進程的100名人排行榜》中,穆罕默德位列第一,牛頓名列第2位,在耶穌之前。
更厲害的是,牛頓活了八十歲,但他的后四十年都在研究神學。也就是說,牛頓的成果都是前半生發展的,22歲左右是個重要時期。
牛頓研究微積分,主要還是為了物理上的計算服務的,我們來看下牛頓是怎么推導微積分:
牛頓的微積分
牛頓歸納微積分的整體思路是:
- 證明求導是不定積分的逆運算,即微積分第一基本定理(《高等數學》同濟版為求積分上限函數的導數)。
- 進而推出牛頓-萊布尼茲公式,即微積分第二基本定理。
1.1 微積分第一基本定理
牛頓嘗試證明下面這個結論:


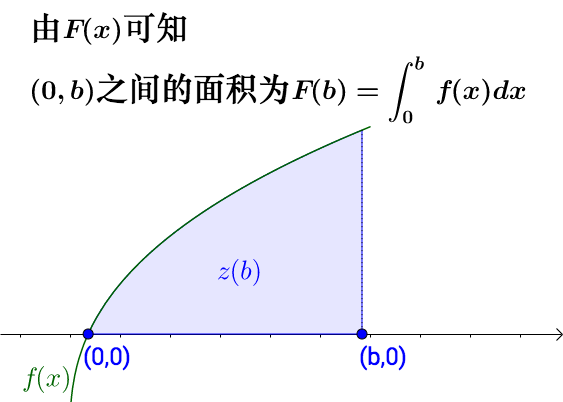
已知函數曲線下,?區間的面積為:

如果把上限 a換為 x,那么曲線下面積就為一個函數,我們稱為積分上限函數:
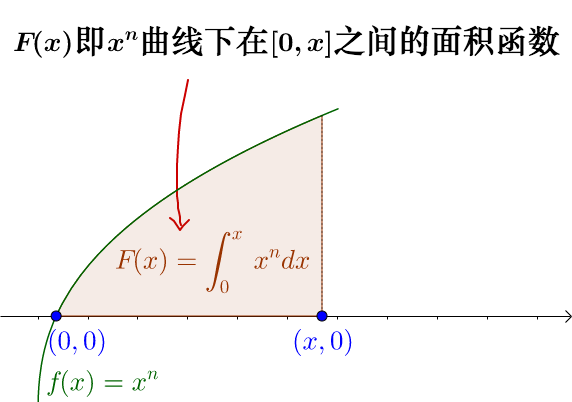


下面我會分別介紹這兩個步驟,從這兩個步驟我們可以分別看出:
- 步驟一,推出微積分第一基本定理
- 步驟二,展示一下牛頓是怎么求解導數的
1.1.1 步驟一
在當時,導數這個詞還沒有,不過有一個等價的詞,就是變化率,因此牛頓就從求 F(x)
的變化率出發。為了求變化率,牛頓是這么思考的:
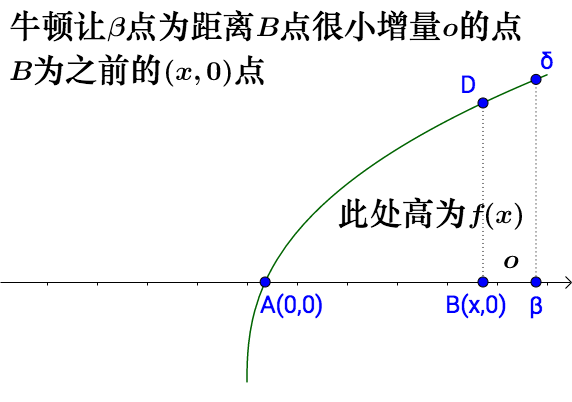
以 B,b為底做一個矩形,圖中虛線圍起來的部分。

可以看出 o越小, 圖上虛線所圍成的的面積越接近 o與f(x)的乘積。
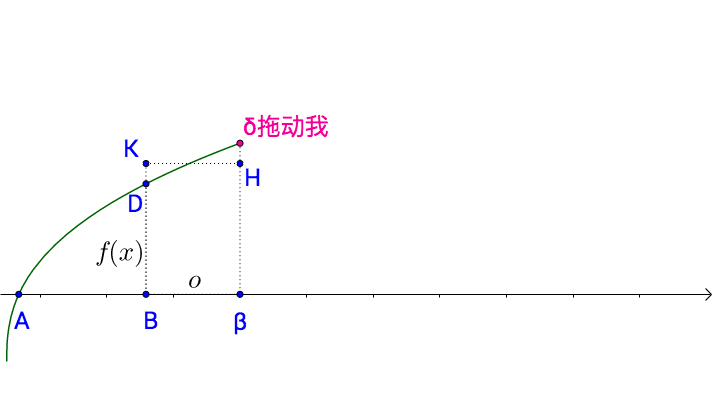
牛頓斷言,當 o足夠小的時候
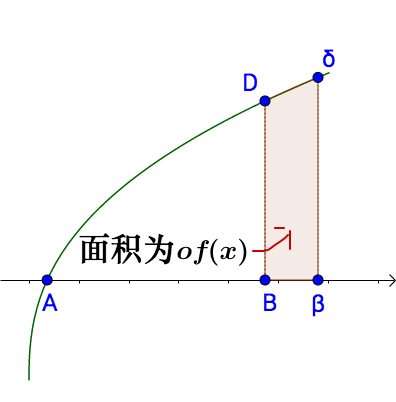
F(x)關于o的增量為o*f(x),根據變化率的定義,

?注意頭上有個小點的為F(x)的流數(這里流數就是指的變化率),也就是現在的導數 。
至此:

實際上到了這里已經得出了微積分第一基本定理:

從這里可以看出,面積函數F(x)實際上是 f(x)的一個原函數。
1.1.2 步驟二
下面就是要計算出f(x)等于多少了。費馬和卡瓦列里計算出了:

替換一下就可以得出:

基于此結論,牛頓繼續推了下去(二項式指的是 n?為自然數,而廣義二項式指的是 n為有理數,廣義二項式公式是牛頓非常得意的一個數學推論):

證明完畢

1.2 牛頓-萊布尼茲公式
順著積分第一基本定理出發,要推出了大名鼎鼎的牛頓-萊布尼茲公式(微積分第二基本定理)就很容易了。


也就是:
積分第二定理最大的意義是大大簡化了運算。
1.3 手稿
下面是牛頓的手稿,可以讓我們看看微積分青澀的模樣:

其他資源
Linux Socket SO_LINGER選項_熊大談技術的技術博客_51CTO博客
百度安全驗證
別慌!這篇微積分教程你一定看得懂!
微積分的歷史(二),起源之牛頓 (zhihu.com)
第二講 牛頓-萊布尼茨公式.ppt
頂級數學家可以“恐怖”到什么程度?_牛頓_高斯_歐拉
數學史話:微積分與牛頓、萊布尼茲 - 知乎
高中大學銜接:反三角函數 - 知乎
高中數學-反三角函數 - 知乎
反三角函數的性質? - 知乎
e與ln是什么函數類型 轉換公式是_高三網
有關“x、e^x、lnx”組合函數的考點與題型歸納
從積分法的誕生到牛頓歸納出微積分學竟然經歷了1800年!一文講透微積分的本質|微分|定理|畫家|詩人|牛頓(布萊克)_網易訂閱



















覆蓋優化 - 附代碼)