Cohen E, Halperin E, Kaplan H, et al. Reachability and distance queries via 2-hop labels[J]. SIAM Journal on Computing, 2003, 32(5): 1338-1355.

Abstract

圖中的可達性和距離查詢是許多應用的基礎，從地理導航系統到互聯網路由。其中一些應用程序涉及到巨大的圖形，但還需要快速的查詢回答。我們提出了一種新的數據結構來表示圖中的所有距離。數據結構的分布方式是，它可以被視為為頂點分配標簽，這樣，一個涉及頂點u和v的查詢就可以只使用u和v的標簽來回答。
我們的標簽是基于圖中最短路徑或所有路徑的2跳覆蓋。最短路徑，這樣的封面是一個集合的最短路徑，這樣每兩個頂點u和v，有一個最短路徑從u連接兩個路徑從S我們描述一個算法的幾乎最優2跳覆蓋一個給定的路徑集合。我們的方法是通用的，可以應用于有向或無向圖，精確或近似的最短路徑，或可達性查詢。
我們使用理論和實驗方法的結合來研究所提出的數據結構。我們實現了我們的算法，并從不同的應用領域的幾個真實網絡上檢查了結果數據結構的大小。我們的實驗表明，標簽的總大小通常并不比網絡本身大多少，而且通常比網絡的傳遞閉包的顯式表示要小得多。

1 Introduction

我們考慮了在有向圖或無向圖中及時回答距離或可達性查詢的問題。我們關注的場景是圖/網絡明確地給我們，我們能夠對它進行一些預處理。生成的數據結構應該相當緊湊，并應該盡可能地加快查詢回答的速度。通常，可用于處理查詢的計算資源比在預處理階段可用的計算資源要弱。例如，在地理導航系統中，預處理可以在大型計算機上完成，而查詢則使用安裝在汽車上的一個弱得多的處理器來回答。
對這個問題有兩個幼稚的解決辦法。首先是預先計算所有可能的查詢的答案，例如，通過求解全對最短路徑（APSP）問題，或通過計算網絡的傳遞閉包。然后，就可以在恒定的時間內回答每個查詢。然而，這并不是一個可行的選擇，特別是對于稀疏網絡，因為為n-頂點圖產生的數據結構將是大小的（n2）。第二種方法是完全不進行預處理，并回答每個查詢，例如，使用單源最短路徑（SSSP）計算。這里的空間要求是最小的，但是回答一個在m個邊圖上的查詢可能需要(m)個時間。
本文提出了一種新的處理方案和相應的查詢回答算法，用于回答可達性和距離查詢。我們的預處理方案生成了一個合理大小的數據結構，即不比原始網絡大多少，并且通常比網絡的傳遞閉包的顯式表示要小得多。考慮到預先計算的數據結構，我們的查詢回答算法可以快速回答距離和可達性查詢，比不進行預處理要快得多。
由我們的預處理算法生成的數據結構是分布式的。我們為網絡的每個頂點分配了一個距離或可達性標簽，這樣我們以后就可以只使用這兩個頂點的標簽來計算兩個頂點之間的距離（或可達性關系）。Peleg [10]、加沃耶等人[4]、Thorup和Zwick [12]都考慮了距離標簽。然而，所有這些論文都只考慮無向圖，并且只考慮最壞情況下的結果。我們主要感興趣的是有向圖，以及在實踐中發生的網絡上所提出的標記方案的性能。
我們的標簽是基于2跳封面的概念。設G = (V；E）是一個（有向或無向）圖。對于每一個u；v 2 V，讓Puv是G中從u到v的路徑的集合（例如，Puv可能是從u到v的所有最短路徑的集合）我們沒有一個跳是一對（h；u），其中h是G和u 2 V中的路徑，跳的手le，是h的端點之一。我們說一個跳H的集合是集合P=的2跳覆蓋[uvPuv，如果對于每個u；v 2 V，如果Puv =；，那么有一個路徑p 2 Puv和兩個跳（h1；u）2 H和（h2；v）2 H，這樣p是連接h1h2。我們將展示如何通過將每個跳映射到其處理節點的標簽中的一個項目，從這樣的封面獲得一個2跳標簽。
每個這樣的項目的性質和標簽的解釋取決于我們想要解決的問題的規格c變體。例如，考慮無向距離查詢。每一組路徑Puv包含u和v之間的所有最短路徑。u的標簽L (u)中對應于跳(h = (u = v0；：：：：vk）的項目為（w (h)；vk），其中w (h)為路徑h的權重。兩個節點u和v之間的距離可以從它們的標簽中得到，通過取兩個權值和在L (u)和L (v)中出現的所有節點的最小和的方法。
因此，標簽的總大小是jHj（我們在這里計算封面上的跳躍數，而不是它們的總長度）。每個距離/可達性查詢都可以及時回答，相應標簽的大小是線性的。因此，平均而言，在O（jHj=n）時間內。
我們證明了確定一個最小大小的2跳覆蓋（因此，也是一個2跳標記）是一個np困難的問題。然而，我們提出了一個有效的和實用的算法，我們實現了，以獲得幾乎最優的2跳覆蓋。該算法返回的2跳覆蓋的大小大于最小可能的2跳覆蓋，最多為一個對數因子。在實際應用中，我們期望該算法的性能比率會更好。
我們的算法產生了任何輸入圖的一個幾乎最優的2跳標記。有些圖可能有較短的標簽，而不是2跳標簽。但是，對于許多有趣的圖族，如平面圖，最優的2跳標記幾乎和最優的標記一樣短。因此，沒有為任何這樣的圖族設計，我們的算法產生幾乎最優的標簽。正如我們的實驗所述，它也可以很好地工作，例如，主要是平面，或主要是樹狀，就像許多實際問題一樣。
我們推測任何n頂點的m邊有向圖都有一個2跳覆蓋，因此有一個2跳標記，總大小為~O（nm1=2）。我們展示了存在任何距離或可達性標記大小的圖（nm1=2）。
我們的方法的一個有用的特性是，通過正確地選擇底層路徑集，可以為最短路徑問題的兩個不同變體產生標簽：可達性或距離，有向或無向，精確或近似的距離，以及對于頂點對的完整或部分集。盡管所有頂點對的精確有向距離標記是最一般的變體，因為所有其他變體都可以簡化為它，但這種區別是重要的，因為約束較少的變體通常享有更緊湊的標記。其中一個例子是有向平面圖：可達性或（1 +）近似最短路徑的2跳標簽大小O（n日志2n）（使用一些輕微的修改構造Thorup [11]）而精確距離，有一個已知的（n4=3）下限任何標簽方案[4]。構造允許更緊湊標記的譜c圖也不是太難的。因此，應該總是為最小約束的適當變體產生2跳標簽。
我們對我們提出的標記方案進行了實驗研究。我們使用了幾個真實世界的網絡，并獲得了很有希望的結果，表明所產生的標簽的大小通常明顯小于顯式表示所需要的大小。

2 Reachability and distance queries

設G =（V；E）是一個具有n個= jV j和m個= jEj的加權圖（可以是有向的，也可以是m個=jEj）。如果（uv）2E是一條邊，我們讓w（uv）為附加該邊的重量（或成本或長度）。在應用中使用的網絡中，附加到邊緣的權值是非負的。然而，我們的方法在存在負權重的邊緣時也有效。我們設（u；v）為圖中從u到v的距離，也就是說，圖中從u到v的路徑的最小權重，如果有一個存在，否則為1。（我們假設在圖中沒有負的權值循環，所以所有的距離都是很好的。）
我們希望對圖G進行預處理，并得到它的緊湊表示，這樣給定一對頂點u；v 2 E，我們就可以快速回答以下查詢：
在圖中有從u到v的路徑嗎？
dist (u；v）：圖中從u到v的距離是多少？有時，我們會滿足（1 +e）近似的距離。
從u發出的哪一條邊是從u到v的（最短）路徑上的第一條邊？
路徑（u；v）：在圖中找到從u到v的（最短）路徑。
可達性查詢當然是（定向）距離查詢的特殊情況，因為當且僅當從u到v的距離是有限時，才有一個從u到v的路徑。如果我們只對可達性性質感興趣，我們可以假設圖中所有邊的權值為0。路徑查詢可以使用重復的第一邊查詢來回答。在某些情況下，有可能加快處理重復的邊緣查詢，如果從u最短路徑包含，比如，邊緣，然后邊緣查詢的處理時間產生它需要更少的時間然后的一個典型的邊緣查詢所需的時間。

3 2-hop labels

一個可能的方案實現上述目標如下：在預處理階段，我們附加到每個頂點u的圖一個相對較短的標簽L(u)，這樣對于任何兩個頂點u和v，兩個標簽L (u)和L (v)將包含足夠的信息來回答所需的查詢。更正式：
定義3.1。（距離標記）一個加權的、有向的或無向的，圖G = (V；E）是一對（L；F），其中L：V！f0；1g和F： f0；1gf0；1g！（IR [ f1g）（E [ f g），對于每個uv2V，如果F（L(u)L(v)=（de），則d=（uv），圖中u到v的距離。如果d=為1，則為e=。否則，e是圖中從u到v的（最短）路徑上的第條邊。標記的總位大小為P v2V jL (v)j，其中jL (v)j為L (v)的長度。最大的標簽尺寸是自然的maxv2V jL (v)j。如果F（L (v)；L(u)可以在O（jL(u)+（+）+）時間內計算，則假設標記方案具有線性復雜度。
可達性標簽也是類似的，和（1 +e）-近似的距離標簽是通過要求（u；v）<=d<=（1 +e）（u；v）：我們關注以下形式的可達性/距離標簽：
定義3.2。（2跳距離標記）讓G =（V；E）是一個加權有向圖，G的2跳距離標記給每個頂點v 2 V分配一個標簽L (v) =（Lin (v)；Lout (v)），這樣Lin (v)是一對的集合（x；（x；v）），其中x 2 V，類似地，Lout (v)是一對的集合（x；（v；x）），其中x 2 V。只要稍微濫用符號，我們也認為Lin (v)和Lout (v)是v的子集，對于任何兩個頂點u；v 2 V，我們要求：
（u；v）=最小值x2Lout (u)\Lin (v)（u；x）+（x；v）：
標簽的大小被定義為P v2V jLin (v)j + jLout (v)j。
對于近似的距離，我們放寬了對minx2Lout (u)\Lin (v)（u；x）+（x；v）（1 +）（u；v）的要求。
對于無向圖，我們可以簡化理解：對于每個頂點v，只有一個集合L (v)對（x；(x)），這樣對于每個u；v 2 V，我們有（u；v）= minx2L (u)\L (v)（u；x）+（x；v）。標簽的大小是P v2V jL (v)j。
一種稍微一般的距離標簽如下：
定義3.3。（Steiner2跳距離標簽）Steiner2跳距離標簽是Lin (v)和Lout (v)分別由形式（x（x(x)和(x)d(x)對組成的標簽，其中x 2 X、x(v)d(x)2IR，以及X是任意的夜間集。我們要求
（u；v）=最小x2Lout (u)\Lin (v) d（u；x）+ d（x；v）
（對于無向圖和近似距離，也可以得到近似的理解。）
請注意，任何2跳距離標記都是斯坦納2跳標記，帶有X = V和d（x；v）=（x；v）。我們還使用了以下2跳可達性標簽的識別。
定義3.4。（2跳可達性標記）設G = (V；E）為有向圖。G的2跳可達性標記為每個頂點v 2 V分配一個標簽L (v) =（Lin (v)；Lout (v)），這樣Lin (v)；Lout (v)V，從每個x 2 Lin (v)到v，從v到每個x 2 Lout (v)。此外，對于任意兩個頂點u；v 2 V，我們應該有：
標簽的大小被定義為P v2V jLin (v)j + jLout (v)j
2跳斯坦納可達性標記也是類似，但我們允許Lin (v)和Lout (v)包含來自任意夜間集X的頂點。
在認知3.1中，我們以位為單位測量標簽的大小。另一方面，在deniten3.2和3.4中，我們通過它們包含的跳數總數來測量2跳標簽的大小。2)我們的2跳標簽，如de ned，不支持初始邊緣查詢。但是，很容易向跳點中添加rst邊緣信息，這樣它們就可以支持這樣的查詢。
給定標簽L (u) =（Lin (u)；Lout (u)）和L (v) =（Lin (v)；Lout (v)），我們可以很容易地計算（u；v），從+(u)（+）jjLin(v)+)時間。（我們保持Lout (u)和Lin (v)按排序順序，并合并為它們的交點。）事實上，我們也可以在O（minfjLout(u)j；jLin(v)j）jg)時間中這樣做，如果我們為集合Lout (u)和Lin (v)保留哈希表。作為2跳可達性標記的示例，考慮圖1中的圖和旁邊表中顯示的2跳標記。我們假設每個頂點v默認都包含在Lin (v)和Lout (v)中。

4 2-hop covers

與2跳標簽密切相關的是圖中路徑集合的2跳覆蓋的概念。
定義4.1。（2跳蓋）讓G = (V；E）是一個圖。對于每一個u；v 2 V，讓Puv是從u到v的路徑的集合（對于無向圖，我們有PuvPvu）。讓P = fPuv g。我們沒有把一個跳變成一對（h；u），其中h是G中的一條路徑，u 2 V是h的端點之一。我們把你稱為跳躍的手柄。如果每一個=；v 2 V有一個路徑，=2，兩個=（h1；u）2=和（h2；v）2=，這樣= h1h2，即=是h1和h2的連接。封蓋的大小為jHj，即H中的跳數。
直觀地說，如果p是兩個跳點路徑的連接，并且跳點的句柄是p的端點，則路徑p可以被兩個跳點覆蓋。通過將帶有句柄v的跳映射到節點v標簽中的一個項目，我們從2跳覆蓋中獲得2跳標簽。因此，這個標簽的大小等于2跳蓋的大小。
此外，通過設置Lin (v) = fx j（（x；v）；v）2 Hg和Lout(v)=fxj（（x；x）；v）2 Hg，我們可以從G中所有路徑集合的2跳覆蓋H中獲得可達性標簽。反之也適用：從G的可達性標簽，我們可以通過向H添加一個相同大小的2跳蓋，一個任意路徑v；如果x 2 Lout (v)，一個任意路徑x組成的跳；如果x 2 Lin (v)，v和端點v。同樣地，我們也可以從G中所有最短路徑集的2跳覆蓋物中獲得2跳距離標簽，反之亦然。我們還可以從所有近似最短路徑集的2跳覆蓋中獲得近似的距離標簽，反之亦然。因此，我們得到了一個最優的所有路徑集和所有近似最短路徑集的大小分別等于2跳的可達性標簽、2跳的距離標簽和2跳的近似距離標簽。
所有路徑的集合、所有最短路徑的集合和所有近似最短路徑的集合的共同性質，使它們的2跳覆蓋對應于2跳標簽如下：
定義4.2。（跳不變性）圖G =（V；E）中的一組路徑P = fPuvg被稱為跳不變性，如果存在一個路徑集合Q，使
對于任意兩個頂點vi和vj，最多有一個路徑qij 2 Q，使vi；qijvj。
只要vi；v1vj；p2vk是P的路徑，那么qij和qjk存在，qij qjk 2 P存在。
引理4.1。由特定頂點對集合（在有向圖或無向圖中）之間的所有最短路徑組成的集合P是2跳不變的。特別是，所有最短路徑的集合都是跳不變的。對于(1 +e（近似最短路徑）和所有有向路徑的集合。
證明：在所有這些情況下，在Q中放置一條連接每對節點的任意最短路徑是最有效的。
定理4.1。在有向圖中尋找最短路徑集合P的最小2跳覆蓋度是一個np困難問題。
證明：我們將3-SAT簡化為有向圖中最短路徑的最小2跳覆蓋問題的決策版本。設S是3-SAT的一個實例，其中包含變量x1、x2、x3、：：：、xn和子句C1、C2、3：：、Cm。我們為2跳覆蓋問題建立了一個實例。圖G由一個樞軸頂點p以及一組可變小工具和子句小工具組成。對應于一個變量x的變量小工具由我們通過添加圓弧（p；bx )和（p；bx )來將pivot p連接到變量小工具。
設C是一個子句C =（X；Y；Z），其中X、Y和Z分別是變量x、y和z的字面意思。對于每個這樣的子句C，我們添加一個頂點C和弧(bX；c）、(b Y；c）和(bZ；c）（即，如果X = x我們加弧(bX；c），如果X = x我們加弧(bX；c），同樣對于y和z）。
對于每個變量x，我們dePaxiexjj2f1；2g，是從ax i到ex j的有向路徑集合。我們也將Ppex j由從p到e x j，j 2 f1的有向路徑組成；2g。我們稱集合Pax i ex j和Ppex j為對應于變量x的變量路徑。對于子句C =（X；Y；Z），我們刪除PbX c、PbY c和PbZ c，分別為包含從bX到c、從bY到c、從bZ到c的單條邊的有向路徑的集合。我們還認為Ppc由從p到c的三條有向路徑組成。我們認為上面沒有提到的所有東西都是空的。
我們聲稱，當且僅當2跳覆蓋實例具有最多5n + 3m大小的解時，3-SAT實例S是可以滿足的。
這一主張的證據如下。假設S是可以滿足的，設f是一個令人滿意的賦值。我們沒有一個2跳的封面H如下。對于每個變量x，如果f (x) = 1，我們將跳（（ax1）、ax 1 )、(b)、(b)和(1)和H（=1）、p）、（=）、c）和（=）和H。可以直接檢查如果f滿足，則H確實是一個覆蓋。H的大小為5n + 3m。
對于另一個方向，設H是一個尺寸為5n + 3m的2跳蓋。覆蓋所有變量Pbxc和Pbxcx和子句C，封面H必須包括3m不同的跳的形式（bX；c），對于每個條款C和文字X 2 C覆蓋對應x的變量路徑我們需要至少5跳組成的弧與變量設備的頂點對應x，和p。由于H是一個大小為5n+ 3m的2跳覆蓋，我們覆蓋每個變量的可變路徑。很容易檢查覆蓋5跳的可變路徑的唯一方法是包括H中的跳點（ax1、bx )、（ax2、bx )、ax 2 )、（p、bx )、p）、（bx、ex 1 )、ex 1 )和（bx、ex 2 )、ex 2 )或（ax2）、（ax2）、（bx、ex 1 )、ex 2 )、ex2）=1，當且僅當前一組跳點在H中。由于H也覆蓋所有子句C的Ppc，因此S必須是令人滿意的真實分配。
然而，如果路徑P的集合是跳不變的，我們就可以單獨得到一個幾乎最優的2跳覆蓋。
定理4.2。設G =（V；E）是一個具有jV j =的圖，設P是G中的一個跳不變路徑集。然后，有一個算法來確定一個2跳覆蓋的P，其大小大于最小的覆蓋最多一個O（log n）因子。
在證明這個定理之前，我們先介紹一下一些符號。如前一樣，讓Puv，對于u；v 2 V，是P從u開始，到v結束的路徑。設BuvV是出現在來自Puv的路徑上的頂點集。（請注意，u；v 2 Buv，如果是Puv =。）一個重新研究的結果表明，對于u；v2v，P的最小2跳覆蓋度的大小僅取決于集合Buv。我們還需要討論最密集的子圖問題，并陳述一些已知的結果。
定義4.3。（最密度子圖）最密集的子圖問題如下：給定一個無向圖G =（V；E）和一個子集的子圖的平均度是最大化的，即一個使jE(S)=jSj最大化的集合，其中E (S)是連接S的兩個頂點的邊的集合。
利用flow技術可以在多項式時間內精確地求解最密集的子圖問題。Lawler [8，第4章]給出了這樣一種算法。由于加洛、格里戈里亞迪斯和Tarjan [3]，目前該問題的最佳可用時間限制是O（mnlog（n2=mn））。將最密集子圖問題簡化為參數最小割問題，然后利用參數極大割算法的運行時間與戈德堡算法的運行時間相同，和Tarjan [5]算法的非參數極大割算法進行求解。
更實際的興趣的是針對最密集子圖問題的一個更簡單的線性時間2-逼近算法，它是對Kortsarz和Peleg [7]提到的算法的一個輕微的修改。根據計算算法迭代地從圖中刪除一個最小度的頂點。這將生成原始圖的n個子圖的序列。該算法返回這些子圖中最密集的一個。不是迪崇拜檢查這個算法可以實現運行在線性時間，這是一個2-近似算法最密集的子圖問題，也就是說，平均度子圖返回至少一半的平均度最密集的子圖。
我們現在可以給出定理4.2的一個證明。
證明：（根據定理4.2），我們將P的一個最小2跳覆蓋的問題轉換為一個最小集覆蓋問題。然后，我們應用貪婪算法和一個覆蓋，最多大于一個對數因子（Chvatal[1]，約翰遜[6]，Lovasz[9]）。產生的一個結果是產生的集合覆蓋實例是巨大的。然而，我們證明，可以將貪婪算法應用到這個集合覆蓋實例，而不顯式地生成它。
我們首先回顧了集合覆蓋問題的貪婪算法的行。集合覆蓋問題的實例是一個地面集T，和一個T的子集的集合S。對于每個S 2 S，都有一個關聯的權重w (S)。目標是建立一個子集US，使[S2U S = T和P S2U w（Si）最小化。針對該問題的貪心算法如下。我們維護未覆蓋元素t0的集合，它被初始化為T 0 = T。在算法的每次迭代中，我們在U中添加一個集合S，它使jS\T 0 j w (S)的比率最大化。我們迭代到T 0 =。
與2跳覆蓋實例對應的集合覆蓋實例構造如下。要覆蓋的元素的地面集合是T = f（u；v）j==g。對于每個頂點w 2 V和兩個子集連接；CoutV，我們有一個集合

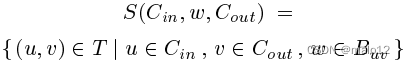
附加到這個集合上的權重是jCinj + jCoutj。頂點w被稱為集合S的中心（Cin；w；Cout）。目標是建立一個覆蓋T的最小總重量集合的集合。（請注意，集合集合的大小是指數級的。）
該集合覆蓋實例等同于2跳覆蓋問題的證明如下：如果H是一個最小尺寸的2跳定向覆蓋，我們讓Cin (w) = fuj（（u；w）；u）2 Hg和Cout(w)=fuj（w；u）；u) 2 Hg。然后，我們可以使用w 2 V的集合S（Cin(w)；w；Cout (w)）來覆蓋集合T。
相反地，我們首先聲稱，我們可以假設為w.l.o.g.最小覆蓋度最多包含一個具有給定中心的集合。如果蓋包含具有相同中心的兩組，即S (C0 in；w；C0輸出）和S (C00 in；w；C00輸出），則可以由組S (C0輸入[ C00輸入；C0輸出[ C00輸出）替換。
因此，設S（Cin(w)；w；Cout (w)）為與w 2 V對應的集合。現在可以通過以下方式設置相應的2跳蓋：（(u)u）當且僅當u 2 Cin (w)和（（wu）u）2H當且僅當u 2 Cout (w)。
接下來我們必須證明我們可以將貪婪算法應用于這個指數大小集覆蓋實例。設t0是T中仍然未被發現的部分。最初是T 0 T。在貪心算法的每一步中，我們都應該得到一個具有最佳比率jS\T 0 j w (S)的集合S。在有向情況下，我們尋找一個集合S（Cin；w；Cout）的比率

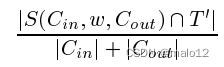
是最大化的。
為了做到這一點，我們，對于每一個w 2 V，集合S (w)在所有集合S（Cin；w；Cout）上最大化上述比率，其中w是它們的中心。我們構造了一個輔助的無向二部圖Gw =（Vw；Ew），我們稱之為w的中心圖。頂點集vw包含兩個頂點的每個頂點v的原始圖g和vout。我們有無向邊（uout）2Ew當且僅當（u；v）2 T 0和w 2 Buv。Gw中的許多頂點可能是孤立的，因此可以從圖中刪除。直接證明了最大化jS（Cout）\T0j=（jCinj+jCoutj=）的問題恰恰是確定Gw最密集子圖的問題。
我們解決了這個問題，計算每個中心w 2 V的S (w)，然后選擇S (w)具有最佳比率的頂點w。然后，我們將相應的集合S (w)添加到封面上，更新t0，并重復，直到t0為空。
由約翰遜[6]，Lovasz[9]和Chvatal[1]表明，貪婪啟發式對集合覆蓋問題的性能比率為Ht，其中t是被覆蓋的元素數，Ht是調和數。對于我們的問題，元素的數量等于頂點對的數量，這樣在它們之間至少有一條路徑。因此，我們得到了一個近似的比值

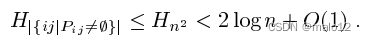
這種構造對無向路徑略有不同。要覆蓋的集合T是一組（無序的）頂點對fu；vg，使Buv =；。對于每個頂點w 2 V和一個子集CV，我們有一個集合S（C；w）= f fu；vg j u 2 C；v 2 C；w 2 Buv g。證明該集合覆蓋問題與我們原來的2跳覆蓋問題是等價的，本質上是對于有向情況：設S（C(w)；w）為w then（（u；w）；w）2 H i u 2 C (w)對應的集合。為了解決集合覆蓋實例，我們感興趣的是S (C；w），它可以最大化jS（C；w）\T0jjCj。我們再次首先為每個w分別解決這個最大化問題。這里的輔助圖Gw =（V；Ew）包含V的每個頂點的一個副本，通常不是二部圖的。我們有邊（uv）2Ew當且僅當（uv）2T0和w2Buw。類似地，最大化jS(w)（C；w）的集合S(w)=jCj的問題就是確定Gw最密集子圖的問題。
我們的逼近算法與Kortsarz和Peleg [7]給出的關于2-扳手問題的逼近算法有相似的成分。
圖2：一個路徑的2跳點覆蓋物。彈跳是虛線或原始邊。菱形表示哪個端點是跳的端點。

4.1 A simple example

為了更好地可視化我們的算法的工作原理，我們演示了它在一種特殊情況下的操作，其中輸入是一個由單個有向路徑組成的圖。我們用連續的整數（1；2；3；：：：：；n）來命名路徑上的節點。考慮頂點j的中心圖Gj。對于每一個i，k，這樣的i < j和k > j在Gj中有一條從iout到親屬的邊，它對應于從i到k經過j的路徑。由x跳l；j引起的誘導子圖的密度使l < j和y跳j；l使l > j是xx+y。對于x和y，它們的和最多為n。
注意，如果我們考慮相應的2跳標簽，那么一個節點的最大標簽（該節點構成標記端點的跳數）是O（log n）。請注意，即使算法傾向于選擇較大的中心圖，相應的標簽也只存儲在\外部的“節點”上。因此，它往往在最大標簽度量上也表現良好。
該算法在樹上的工作原理類似，迭代地選擇子樹的重心作為一個中心。因此，生成標簽大小為O（n log n）的最大標簽大小為O（log n）的標記，我們的算法實際上產生了最佳跳標簽。

4.2 Speci c graph families

我們已經看到，我們的算法為所有樹（對于問題的任何變體）生成大小為O（n log n）的2跳標記。這與任何樹標記的位大小的（n log2 n）的下界相匹配，由于加瓦耶等人[4]。
其他一些圖族已知具有緊湊的2跳標記：具有大小為O（n）的分隔符分解的圖具有大小為O（n1+log n）的2跳標簽（例如，參見[2]）。小分隔符圖的最優2跳標記可能是o（n1+log n）。（如果我們的猜想5.1是真的，情況就就是這樣。）
對于平面圖，Thorup [11]表明O（n log n）大小的可達性和近似的距離標簽是可能的。根據他的構造，有相應的大小為O（n log2 n）的2跳標簽。我們沒有發現2躍可達性標記的匹配下界，因此，對于平面圖，有可能存在大小為O（n log n）的最優2躍可達性標記。Thorup的結果特別有趣，因為在平面圖的精確距離標簽上有一個（n4=3）的下界。
另一個特殊的家族由有界度+的圖組成，對于每一對頂點，它們之間至少有一條路徑，長度最多為==logdn+（logd+）邊。例如，一個隨機d正則圖具有高概率的性質。對于這樣的圖，我們可以通過選擇每兩個節點的跳（（v；u）；v）和（（v；u；u）；u）得到大小為O（n1：5+）的2跳標簽，這樣最多有一個dD=2e邊從v到u的路徑。觀察總跳數為O（ndD=2）=O（n3=2+）。

5 Lower bounds on reachability and distance labelings

在本節中，我們證明了有向圖中可達性標簽和2跳可達性標簽大小的下界。我們證明的界也適用于有向圖和無向圖中的距離標記，并且可以直接推廣這些情況下的證明。我們從下面簡單的引理開始，它給出了任何可達性標記的大小（不一定是2跳可達性標記）的下界。
引理5.1。任何可達性標記方案都必須分配一些總大小（m log（n2 =m））位的n頂點m邊圖可達性標簽。
證明：考慮頂點集合V = f1上的所有有向m邊圖；2；：：：；ng，其中所有邊都從V1 = f1；2；：：：；n=2g到V2 = fn=2 + 1；n=2 + 2；：：：；ng。（假設n為偶數。）有
請注意，引理5.1證明中考慮的圖族中的每個圖都可以被分配總大小為O（m log n）位的2跳可達性標簽。我們簡單地讓Lout(v)=fu2V2j(v)2Eg對于每個v 2 V1，Lin (v) = fvg為每個v 2 V2，所有其他集合都是空的。因此，2跳可達性標簽對于這類圖幾乎是最優的。下面的推論總結了這一討論，并表明2跳標簽在以下意義上幾乎是最優的。
推論5.1。設g (n；L）為大小為L (L log n位）的2跳標簽（距離或可達性）的n個節點圖的集合。然后，任何通用的標記方案都會在g (n；L）上分配最大大小（L log（n2 =m））位的標簽。
證明：考慮在引理5.1的證明中所考慮的圖族，其中有n個節點和L條=m條邊。這些圖有大小為l的2跳標簽。推論遵循引理的證明。
接下來，我們使用引理5.1來獲得可達性標簽的總大小的一個更強的下界。
定理5.1。任何可達性標記方案都必須分配給一些具有n個頂點和m個邊邊（nm1=2）位的圖。9
證明：考慮以下形式的圖：從頂點集V1和V2上的二部圖開始，其中jV1j=jV2j=m1=2，m=2有向邊從V1到V2。接下來，使V1的每個頂點成為帶有n=m1=2葉子的星的中心。所有這些葉子都是不相交的，這些葉子的邊都指向V1的頂點。同樣地，使V2的每個頂點成為帶有n=m1=2葉子的星的中心。這一次的邊緣被指向遠離V2的頂點。此圖中的頂點總數為2m1=2n=m1=2+2m1=2=2（n+m1=2）=(n)，邊數為2m1=2n=m1=2 + m=2 = m=2 + 2n = (m)。（注意，nmn2，因此，m1=2n。）
設Ui，對于1=m1=2，是由每顆星的第i葉組成的集合。對于每一個i，限制于Ui的可達性關系與集合v1上的可達性關系是同構的[v2]。從引理5.1可以得出，對于至少一個這樣的圖，我們需要總大小至少為(m)位的可達性標簽。因此，附加到所有頂點上的標簽的總大小必須至少為（n=m1=2m）=（nm1=2）位。
我們的下一個引理將允許我們在2跳可達性標記的大小上得到一個比定理5.1中的一個稍微更好的下界。該引理建立了一組路徑的最優2跳覆蓋層大小的下界。為了指定這個引理，我們需要以下定義。給定一個路徑和v2v的集合P，我們將hv (w)是通過P中的路徑從v到達的頂點數。我們也將hv (w)是通過P路徑到達v的頂點的數量。形式上，hv (w) = jfu j w 2 Bvugj，和hv (w) = jfu j w 2 Buvgj。對于每一對節點（；），我們沒有覆蓋的能力

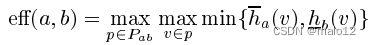
引理5.2。為任何一個2跳的覆蓋

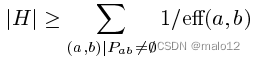
證明：任何一對（a；b）最終被2跳覆蓋。其中一個跳數最多參與e（a；b）路徑。因此，如果每個跳的成本在它所覆蓋的對之間劃分，（a；b）的份額至少為1=e (a；b）。因此，跳數的總數至少為P ab 1=e（a；b）。
對于2跳可達性標簽，我們可以得到比定理5.1中的界略強的下界。在定理5.1中，（nm1=2）的下界是標簽的位的大小，是否在下面的定理中，下界是2跳標簽的總跳數。
定理5.2。存在n個頂點的m邊圖，任何2跳可達性標記方案的總大小必須為（nm1=2）。
證明：我們所考慮的圖是在定理5.1的證明中所使用的圖的一個子集。我們從jV1j = jV2j = m1=2的完全二部圖開始。和前面一樣，我們把V1和V2的每個頂點作為一個有n=m1=2葉子的恒星的中心。下面使用引理5.2進行證明。
最后，我們展示了一些具有較大的2跳可達性標簽的圖具有更短的斯坦納標簽。
推論5.2。存在一組大小為O (n)的Steiner可達性標簽的圖，其中最合適的2躍可達性標簽的大小為（nm1=2）。
證明：定理5.2的證明中的圖可以看作是4層圖，當且僅當u的層低于v的層時，才可以從u得到v。我們使用集合X=fx1；2；x1；3；x1；4；x2；3；x2；4；4gxi；j將i層所有v放在Lout (v)中，j層所有v放在Lin (v)中。
一個類似的，稍微涉及一些的結構，可以用來生成O(n)結構的無定向均勻加權版本大小的Steiner標簽：
推論5.3。存在一組大小為O (n)的無向圖，其中最合適的2跳距離標簽大小為（nm1=2）。
我們推測定理5.2中給出的界是最可能的：
猜想5.1。設G =（V；E）是一個具有jV j = n和jEj = m的有向圖，設P是G中al l最短路徑的集合，然后有一個大小為O（nm1=2）的2跳覆蓋。

6 The Pairs-Cover problem

定理4.2證明中的算法適用于以下更一般的問題：
問題6.1問題。（對蓋）輸入：P1Pk，其中每個Pi是一組對或三組整數。輸出：一組最小大小的整數對，這樣對于每一個i = 1以下內容：
存在一個三重（cj）2Pi，使（ci）2H和（cj）2H，或
存在一對（ci）2Pi，使（ci）2H。
計算跳不變路徑集P的2跳覆蓋的問題可以映射到以下對覆蓋實例：讓V = fv0；：：：；j在對覆蓋實例中映射到另二P。
對于Pvivj中某個路徑上的內部節點的每個vc，我們將以下對/三元組附加到相應的P中：（對于無向圖或有向圖，映射略有不同）
對于有向路徑：我們在P中包括三重（c；n + i；j）和對（i；j）和（j；n + i）。
對于無向路徑：我們包括P中的三重（c；i；j）和對（i；j）和（j；i）。
我們對對覆蓋實例的輸出H解釋如下：如果（c；i）2H（i<），則將跳（vc；vi)；vc)放置在蓋中。(回想一下，由于P是跳不變的，所以跳可以是指定的通過他們的端點。)對于無向實例，跳變包含無向路徑。對于有向實例，跳點包含有向路徑。我們也可以有一對（c；i）2 H和（n）在這種情況下我們重新寫（+）2+。在這種情況下，我們將跳（+）、vc)放在蓋子上。
我們現在提到這個框架所涵蓋的另一個自然問題。我們首先考慮2跳蓋問題的一個變體，其中跳躍沒有句柄。因此，每一跳都僅僅是一條路徑，而Puv則是如果有P 2 Puv和兩條路徑h1；h2 2 H，使P = h1h2。請注意，任何帶有手柄的解決方案都可以通過省略手柄轉換為沒有手柄的解決方案。相反，和通過引入兩個端點作為句點的兩個跳點，沒有句柄的解決方案可以轉換為有句柄的解決方案。因此，得到了與手柄有關的變體的最優解Es最多是沒有句柄的變體的兩倍。因此，我們的貪婪算法可以應用于沒有句柄的版本，盡管在近似比中損失了另一個因素2。奇怪的是，似乎沒有對貪婪算法的自然修改，為沒有句柄的變量得到相同的近似比。
有手柄的變體有更好的標記應用程序，因為有把手的2跳蓋和2跳標簽之間有1-1個對應關系，但是沒有手柄的變體可以有應用程序。
這樣一個可能的應用程序是以下問題
問題第6.2節中。（最小2跳表示）設P是字符串的任意集合。P的最小2跳表示是一組子字符串H，這樣每個字符串s 2 P都是一個連接兩個串的= h1h2。

7 Implementation

我們的實現分兩個階段計算封面。第一階段不不同應用（即可達性，近似或精確，有向或無向距離），并產生一個成對覆蓋問題的實例。第二階段是針對成對覆蓋問題的近似算法。

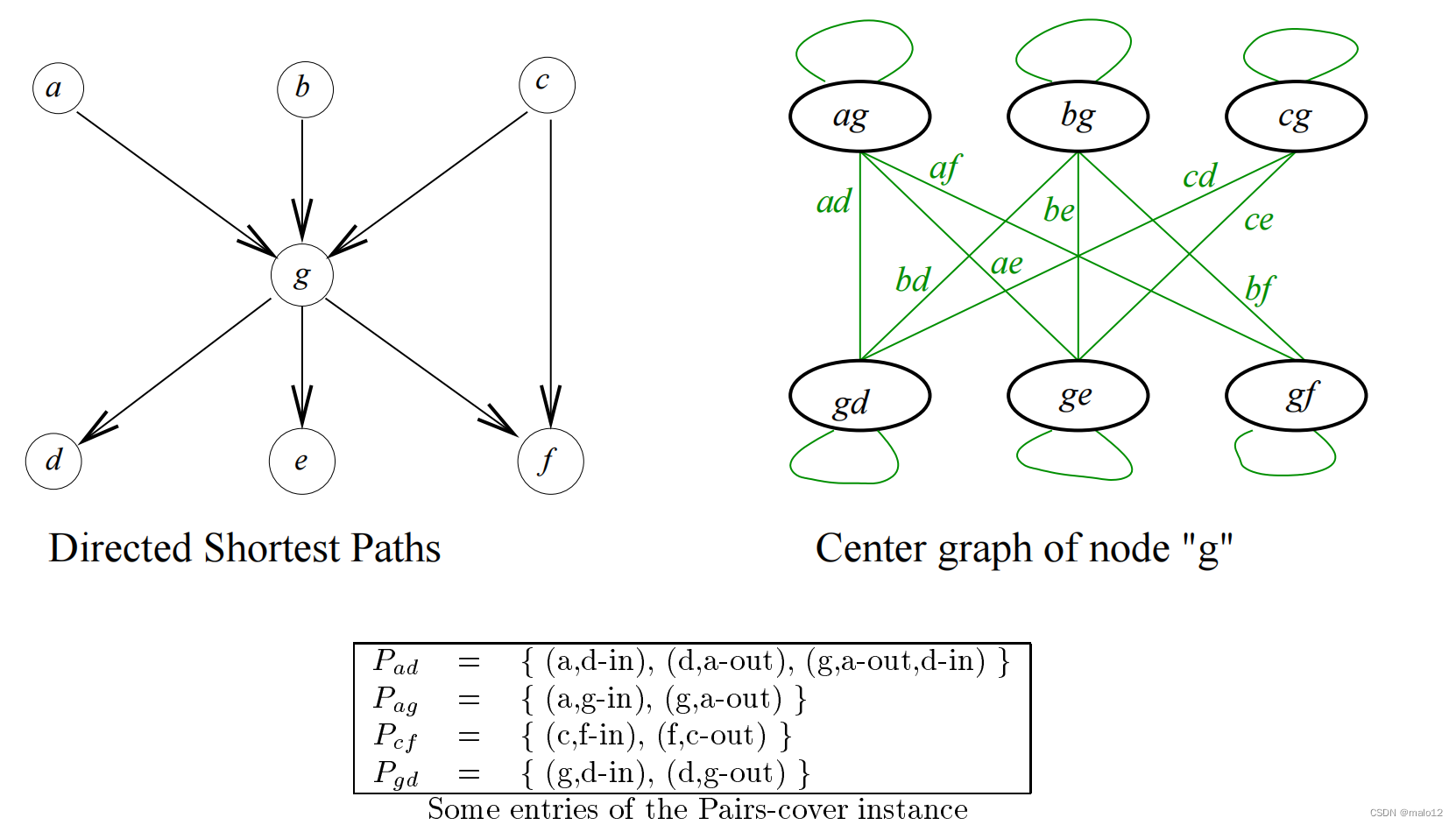
圖3：這是一個構造圖上有向最短路徑問題的一個實例的成對覆蓋實例和中心圖的示例。圖中有7個節點，分別標記為fa；b；c; d; e; f ; gg.這些圖中的夜間距離由7對距離為1的有序對和8對距離為2的有序對組成。相應的對覆蓋實例有一組對/三元組的fo到達這15個有序的節點對。表中顯示了一些條目；其他條目是對稱的：長度為2的所有最短路徑的Pxy條目d與Pad對稱；Pbg和Pcg與Pag對稱；Pge和Pgf與Pgd對稱。該圖顯示了中心g的中心圖。在這個中心g中有6個節點raph，對應于有序對的最短路徑；gf g。在成對覆蓋實例中，這些跳數用a出、b出、c出、d出、ein和fin表示。的邊緣中心圖是有序對，其中兩個跳構成最短路徑；同樣地，如果三重（gx出，yin）(或（gy出，x出）相同，xy標記一條邊s-cover實例。自循環對應于由單個跳點組成的路徑。通過選擇所有節點，得到了這個特定中心圖的最密集子圖；這個子圖因此涵蓋了14個最短路徑使用6跳。請注意，Pcf（從c到f的路徑）沒有被這個中心圖覆蓋，因為沒有穿過節點g的最短路徑。這條路徑可以通過一個s來覆蓋在c的中心圖或中心圖關閉中的ingle跳（具有自循環的單個節點）。在這種情況下，最小的2跳覆蓋物由7跳組成。
第二個階段然后構建一個中心圖的數據結構：對于在某些三組中作為第一個坐標出現的每個數字，我們將一個中心關聯起來。對于每個中心c，我們構造一個(u中心圖。當且僅當輸入中存在一對（c；i）或三重形式（c；；i)或（c；i；）時，c的中心圖中存在一個節點i。對于每個三重（cij）都有一個c的中心圖中的邊緣（i、j）。對于每一對（c；i），在中心圖c中的節點i上有一個自循環。圖3提供了一個構造中心圖的例子。
該算法通過迭代進行，每次迭代的基本操作是子圖選擇：我們選擇一個中心圖，并選擇剩余節點的子集事件剩余的邊緣。選定的節點將被刪除。所選的子圖實際上是這個中心圖中的一個（近似的）最密集的子圖。我們實現的近似最密集的子圖(ADS)在中心圖的大小（邊和節點的數量）上是線性的：節點按剩余度（最初使用桶排序）進行排序，每條邊被一次查看。
每個輸入集P\負責“位于兩個中心圖中的許多邊（每條這樣的邊對應P`中的三重或一對）”。在我們的數據結構中，所有這些邊都是鏈接的(通過doub的鏈接列表)。一旦選擇了其中的一條邊，集合P就被認為是被覆蓋的，并且所有這些鏈接的邊都被從它們各自的中心圖中移除。因此，子圖的選擇在一個中心-圖可能導致刪除其他中心圖上的邊。
主循環引導中心圖的選擇，從中選擇一個子圖。中心被堆地維護。中心c的鍵是最大的邊與節點的比率中心圖Gc的精確計算的ADS。堆通過在每個中心圖中的ADS計算進行初始化。主循環重復以下步驟，直到所有路徑都被覆蓋(所有中心圖的e橋被移除）：
從堆中刪除最大鍵的中心c。
如果自執行上次ADS計算以來從中心圖Gc中刪除邊，則重新計算ADS，c用一個新的鍵放在堆中。
否則，如果中心圖形未被觸及，則選擇ADS。如果未選擇的邊保留在Gc中，則計算一個新的ADS，并使用一個新鍵將c插入到堆中。
為了使這個實現能夠正確地工作，在每一步中選擇一個（近似）最小鍵的中心是很重要的。要看到這一點，請注意一個中心圖的鍵(邊的比率與最密集子圖中的節點)只有在從圖中刪除邊時才能減少。
我們實現了貪婪集覆蓋算法的定理4.2中的證明：算法選擇了幾個對應于sa的子集ME中心：S (C1、w）、S (C2、w）、：：：S (Ck、w），與剩余子集S (C、w）的比率更新為

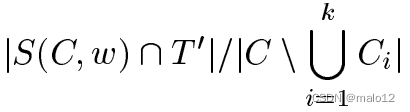
（而不是jS（C；w）\T0j=jCj。）其中t0是中心圖Gw中未覆蓋邊的集合。這是通過刪除已經從中心圖中選擇的節點來實現的(注意，邊只有在選擇兩個端點時才被刪除)。
觀察，這個比率的分子可以隨著其他中心的選擇而減少。分母也可以減少，但只是因為從同一個中心選擇了一個子集。即使與一個特定子集相關的比率可能會增加，但很容易看到，它永遠不會超過來自同一中心的最近選擇的最密集的子圖(如果是，那么這個子集與最近最密集的子圖相結合，就會產生一個更密集的子圖，因此存在矛盾)。因此，一個中心的最密集子圖的最大比率是非遞增的。當一個中心被放回堆中時，我們會計算出一個新的最密集的子圖，因此我們的堆實現仍然可以找到一個具有最大比率的中心。
在我們的數據集上，這個變體比一個子集的比率的分母保持為｜C｜的變體表現得更好。我們證明了最壞情況下的近似比與其他變體相同：
引理7.1。這種變體達到了O（log n）的最壞情況近似比。
證明：對于每一個集合S =（CS；w），設LS是在前幾輪算法中已經選擇的CS的元素。設Sk是我們的算法所使用的集合，按這個順序排列。缺點添加了一個元素v第一次被一個集合=覆蓋。我們讓wv = jCSnLSj jS\T 0 j。請注意

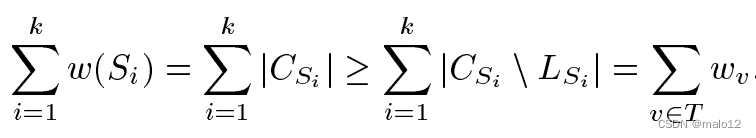
因此，我們可以證明，當是所覆蓋的第j個元素時，那么wvjOPTTj：；Ok0是一個最優覆蓋的集合，其中每兩個集合都有兩個不同的中心。顯然，Pk0 i=1 jCOi j = OP T。此外，Pk0 i=1 jOi \ T 0 jjT 0 jjT j第一個組Oi，這樣

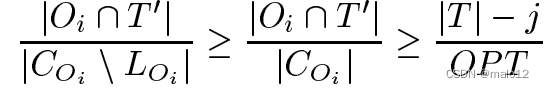
通過對貪心算法的認識，覆蓋v的集合S也將滿足jS\T 0 j jCSnLSjjTjj

8 Experiments

我們使用兩種合成網絡和真實網絡來評估我們的標記算法。我們的數據集的選擇是由我們的標簽方案的兩個重要應用指導的，即路由和地理導航系統對于地理導航，距離查詢可以告訴用戶到達所需目的地的時間或距離。第一邊查詢可用于生成逐匝驅動目錄生態系統。
針對在通信網絡中傳輸的數據包的路由表構成了距離標簽的另一個應用。該模型是，每個數據包都攜帶其目標標簽和當前路由器通過考慮當前路由器上的標簽和目標標簽，獲得下一跳，如果需要，則獲得\距離”。這有點類似于現在的互聯網路由的執行方式： each數據包攜帶其目標ip地址。路由器在其本地路由表中查找ip地址（最長的pre x匹配），以獲得下一跳。然而，路由表正在增長在尺寸方面至于網絡的結構，它們通常的直徑很小。對于as3間圖，圖的核心具有很高的擴展性，而intra-AS網絡可以幾乎是平面的。
ISP-net是一個大型骨干ISP（因特網服務提供商）的網絡。網絡的節點和（有向）邊緣對應于路由器和鏈路。這個特殊的ISP使用OSPF(開放的最短的路由，邊權值是鏈接的OSPF權重。
BGP是由BGP（邊界網關協議）路由器發布的（定向）路徑集4。網絡的節點都是從核心可到達的互聯網上的自主系統（AS）。路徑s都是廣告中的路徑。5我們只考慮3個或更多跳的路徑，因為通過在每個節點上的邊緣信息可以重建更短的路徑。
Roads是阿爾卑斯州（美國）的路線圖，從老虎普查數據[13]。這個圖是無向的，其權值對應于實際的距離。
Grid-k是一個合成網絡。底層網絡是一個k-k個網格。邊緣以曼哈頓的方式指向，偶數和奇數行邊指向相反的方向，同樣，偶數和奇數列邊-邊緣指向相反的方向。邊緣權值從[1；100]中均勻隨機選擇的。
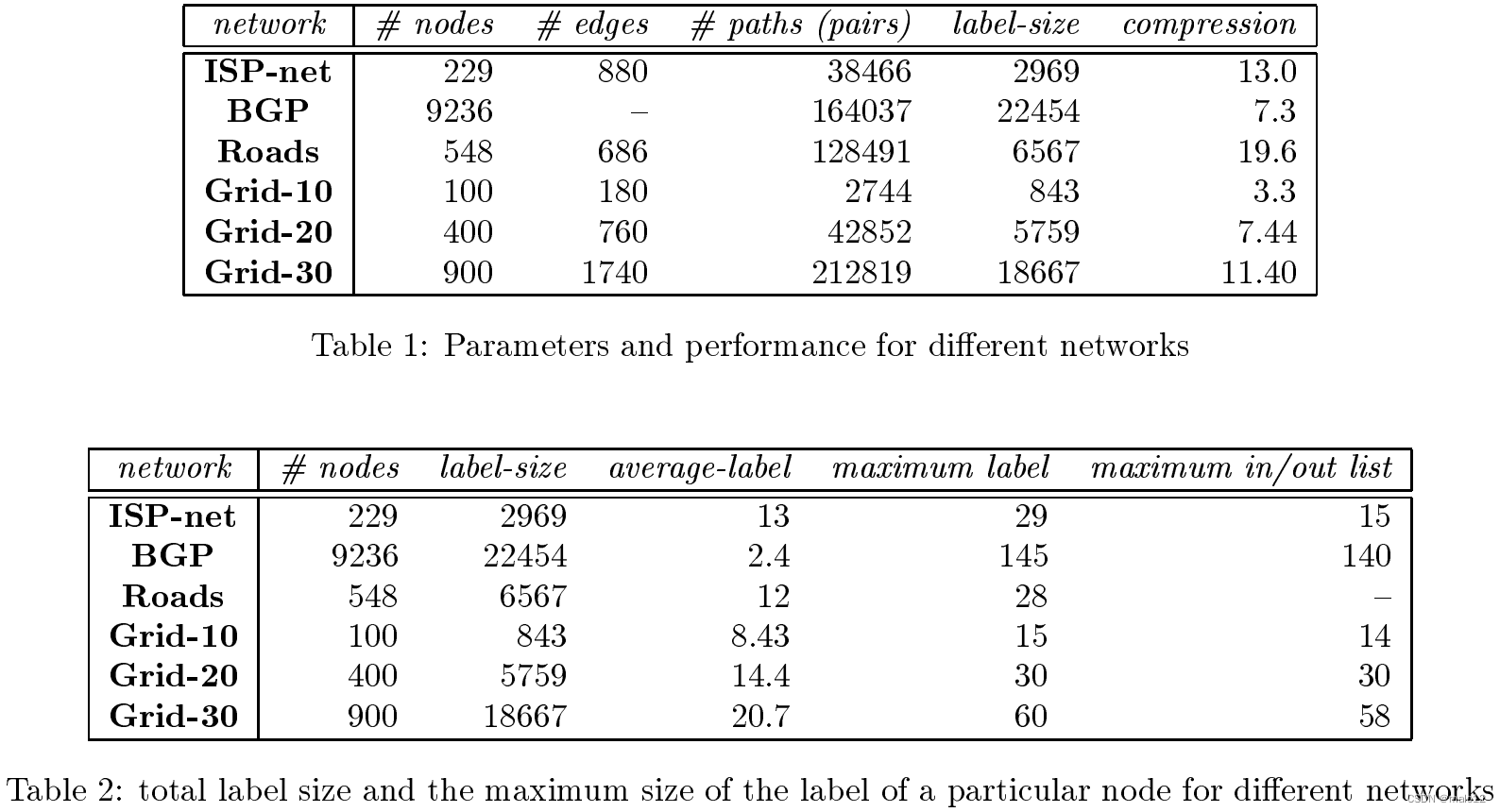
表1列出了每個網絡的節點數量、邊數、從一個路徑到另一個路徑的節點對的數量，以及標簽的總大小（跳數）。補償對比是對數與標簽總大小之比。壓縮比隨圖的大小和結構而變化，在3到19.6之間。一般來說，我們期望對于較大的圖，會有更好的比率。特別地，我們的分析表明，對于平面k網格圖，標簽的總大小為O（k3），而顯式表示為（k4），因此比率為至少(k)。
到目前為止，我們考慮了標簽的總大小。另一個感興趣的參數是特定節點的最大標簽大小。這個參數對于分布式應用程序尤為重要。這也是相關的，因為實際計算的距離標簽的大小是線性的。對于有向圖，我們還考慮列表內或外的最大大小節點的t。表2列出了不同網絡的平均和最大標簽大小。雖然為了最小化總標簽大小，我們的算法似乎也在最大標簽度量方面也表現良好。
另一個有趣的問題是關于標簽的大小對被覆蓋路徑的數量的依賴性。我們的算法可以被設置為在任何給定的路徑部分被覆蓋后停止(實際上，即使在這種情況下，也能提供相同的性能保證。)這種依賴性似乎與Zipf相似（例如，20%-25%的跳數覆蓋了一半的路徑）。

9 Concluding remarks

我們對有向圖和無向圖引入了簡單和自然的距離和可達性標記方案。我們的標簽是由圖中路徑集的2跳覆蓋推導出的。我們給出一個eci構造一個2跳覆蓋的大小比最小的2跳覆蓋大最多O倍（log n）的ent算法。我們推測存在一個尺寸為~O（nm1=2）的2跳覆蓋層具有n個頂點和m條邊的任意加權有向圖中的最短路徑集。證明或反駁這一猜想，也許是剩下的最有趣的問題。我們還演示了通過使用地理導航和互聯網路由等應用的合成和真實網絡的實驗分析，我們的方案。