???? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???????????????🎬慕斯主頁：修仙—別有洞天

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?💜本文前置知識：?紅黑樹

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????????????? ??今日夜電波：漂流—菅原紗由理

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 2:55━━━━━━?💟──────── 4:29
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????🔄 ? ?? ? ? ? ?? ? ????

??????????????????????????????????????💗關注👍點贊🙌收藏您的每一次鼓勵都是對我莫大的支持😍

---

目錄

一、前言

?????????map和set的底層原理????????

?二、紅黑樹的封裝

? ? ? ? ?通過模板使得map和set都可復用紅黑樹

? ? ? ? ?迭代器類

????????operator++()

????????operator--()?

? ? ? ? 紅黑樹類?

? ? ? ? 仿函數

????????map?

? ? ? ? set

? ? ? ? ?封裝后的紅黑樹

? ? ? ? ?begin()和end()

? ? ? ? ?通過仿函數來控制要比較的值

? ? ? ? ?完整封裝?

三、map和set的封裝

????????封裝后的set?

? ? ? ? 封裝后的map?

?四、完整代碼

? ? ? ? RBTree.h

? ? ? ? myset.h?

? ? ? ? mymap.h

---

一、前言

? ? ? ? ?本文主要敘述基于紅黑樹對于map和set的封裝實現，需要有紅黑樹的知識前提。由于前面作者對于紅黑樹主要只是模擬實現了插入的功能。因此本文也只是實現map和set相應的功能，本文的主要要點在于map和set的封裝以及迭代器中++和--的實現。

?????????map和set的底層原理????????

????????C++中的map和set都是STL中的關聯容器，都基于紅黑樹實現。其中set是K模型的容器，而map是KV模型的容器,本文主要講述用一棵KV模型的紅黑樹同時實現map和set。map和set都使用紅黑樹的基本操作，時間復雜度為O(log n)，其中n為元素數量。因此，map和set都是高效的關聯容器。

?二、紅黑樹的封裝

? ? ? ? ?通過模板使得map和set都可復用紅黑樹

? ? ? ? 可以看到我們定義了一個模板參數T，通過T的類型變化來改變紅黑樹中每一個節點的值，從而控制整顆紅黑樹的復用。?

enum Colour
{RED,BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}
};

? ? ? ? ?迭代器類

? ? ? ?迭代器實際上是對于指針進行操作，因此我們實例化并且重新命名了節點類的指針Node,由于迭代器分為是否常量迭代器，對此我們額外定義了兩個模板參數Ref、Ptr用于控制其中重載運算符 T& operator*() 和?T* operator->()。當我們實例化時，區分Ref是const T&還是T&、Ptr是const T*還是T*。后面RBTree中會有所體現。在迭代器中，其中，operator*和operator->返回指向節點的指針，operator++和operator--實現前后綴++/--運算符，operator==和operator!=用來比較兩個迭代器是否指向同一個節點。?

? ? ? ? 以下為大致實現的功能：

template<class T, class Ref, class Ptr>
struct __TreeIterator
{typedef RBTreeNode<T> Node;typedef __TreeIterator<T, Ref, Ptr> Self;Node* _node;__TreeIterator(Node* node):_node(node){}Self& operator--();Self& operator++();Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}};

????????operator++()

????????對于map和set的遍歷我們默認都是中序遍歷，也就是左子樹 根 右子樹。因此對于++操作我們首要的是找到下一個節點，則這個下一個節點便是在這個節點的右子樹，也就是而下一個節點的準確位置為：這個節點的右子樹的最左節點（為什么呢？因為左 根?右我們將這個節點看作為根，則下一個節點位置為右子樹，而右子樹的第一個節點則為最左的節點）。?當這個節點的右為空，意味著包括這個節點在內的左 根 右都遍歷完了，那么我們就需要向上遍歷。則需遵循以下：如果孩子是父親的左就返回父親（這就是意味著遍歷完了左 接下來要遍歷 根），否則就繼續向上遍歷，如果走到nullptr那就是遍歷完成。

總結一下遍歷規則：

1、如果_node的右不為空，找右孩子的最左節點

2、如果_node的右為空，如果孩子是父親的左就返回父親，否則就繼續向上遍歷，如果走到nullptr那就是遍歷完成

	Self& operator++(){if (_node->_right){// 下一個就是右子樹的最左節點Node* cur = _node->_right;while (cur->_left){cur = cur->_left;}_node = cur;}else{// 左子樹 根 右子樹// 右為空，找孩子是父親左的那個祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

????????operator--()?

? ? ? ? ?和上面的operator++()相似，但是我們的遍歷順序變為了右子樹 根 左子樹。

總結一下遍歷規則：

1、如果_node的左不為空，找左孩子的最右節點

2、如果_node的左為空，如果孩子是父親的右就返回父親，否則就繼續向上遍歷，如果走到nullptr那就是遍歷完成

	Self& operator--(){if (_node->_left){Node* cur = _node->_left;while (cur->_right){cur = cur->_right;}_node = cur;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

? ? ? ? 紅黑樹類?

? ? ? ? ?從之前我們所學習的紅黑樹的模擬實現我們可以知道，紅黑樹的插入等等操作中會用到對于key的比較。對此，set和map的比較要求是不同的，set可以直接用key進行比較，而map中對于pair的比較是先按first比較再比價second，而我們想要的結果是只比較first，因此我們定義了個KeyofT來對map和set進行區分。這個KeyofT則是通過傳遞仿函數來進行控制對于要比較值的轉換。

// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, T>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __TreeIterator<T, T&, T*> iterator;typedef __TreeIterator<T, const T&, const T*> const_iterator;iterator begin();iterator end();const_iterator begin();const_iterator end();//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data);Node * Find(const K & key)private:Node* _root = nullptr;
};

? ? ? ? 仿函數

????????注意：這里的仿函數是在map和set中定義的，我們在map和set中的迭代器實際上是就是間接的控制了RBTree的迭代器。

????????map?

		struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};

? ? ? ? ?set

		struct SetKeyOfT{const K& operator()(const K& key){return key;}};

? ? ? ? ?封裝后的紅黑樹

? ? ? ? ?begin()和end()

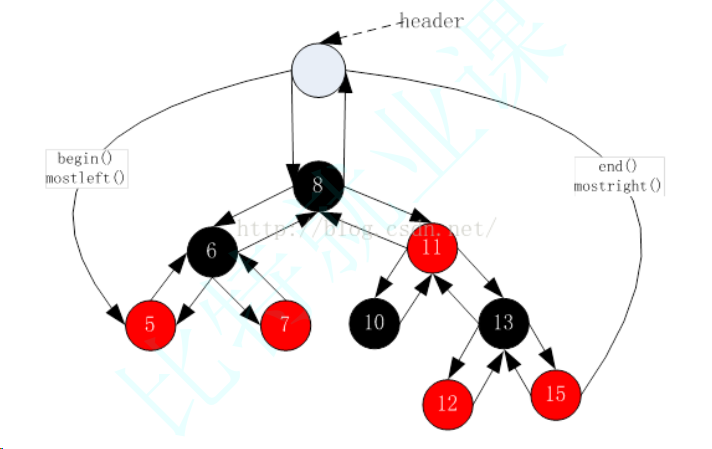
?????????STL明確規定，begin()與end()代表的是一段前閉后開的區間，而對紅黑樹進行中序遍歷后，可以得到一個有序的序列，因此：begin()可以放在紅黑樹中最小節點(即最左側節點)的位置，end()放在最大節點(最右側節點)的下一個位置，關鍵是最大節點的下一個位置在哪塊？能否給成nullptr呢？答案是行不通的，因為對end()位置的迭代器進行--操作，必須要能找最后一個元素，此處就不行，因此最好的方式是將end()放在頭結點的位置：

? ? ? ? ?雖然但是，作者還是將end()給了nullptr，事實上勉強還是可以用的哈哈哈...

	iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}

? ? ? ? ?通過仿函數來控制要比較的值

? ? ? ? ?注意：這里對于insert以及find中都定義了一個KeyOfT kot; 這個就是上面所提到的用于轉化用于比較的數據的仿函數的定義。

?????????其中對于insert有點需要注意：我們運用了pair中的特性，用pair<Node*, bool>接收了make_pair(newnode, true)的返回值，用pair構造了一個新的pair而不是拷貝構造了一個pair。后續會提到為什么（在set封裝中）

	//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}// 新增節點給紅色cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//     g//   p   u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上更新處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 單旋//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 雙旋//     g//   p//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else  // parent == grandfather->_right{//     g//   u   p //          c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p //     c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}Node * Find(const K & key){Node* cur = _root;KeyOfT kot;while (cur!= nullptr){	if (kot(cur->_data) < key){cur = cur->_left;}else if (kot(cur->_data) > key){cur = cur->_right;}else{return cur;}}return nullptr;}

? ? ? ? 完整封裝?

// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, T>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __TreeIterator<T, T&, T*> iterator;typedef __TreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}// 新增節點給紅色cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//     g//   p   u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上更新處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 單旋//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 雙旋//     g//   p//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else  // parent == grandfather->_right{//     g//   u   p //          c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p //     c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}// 根節點->當前節點這條路徑的黑色節點的數量bool Check(Node* root, int blacknum, const int refVal){if (root == nullptr){//cout << balcknum << endl;if (blacknum != refVal){cout << "存在黑色節點數量不相等的路徑" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "有連續的紅色節點" << endl;return false;}if (root->_col == BLACK){++blacknum;}return Check(root->_left, blacknum, refVal)&& Check(root->_right, blacknum, refVal);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;//參考值int refVal = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refVal;}cur = cur->_left;}int blacknum = 0;return Check(_root, blacknum, refVal);}int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}size_t Size(){return _Size(_root);}size_t _Size(Node* root){if (root == NULL)return 0;return _Size(root->_left)+ _Size(root->_right) + 1;}Node * Find(const K & key){Node* cur = _root;KeyOfT kot;while (cur!= nullptr){	if (kot(cur->_data) < key){cur = cur->_left;}else if (kot(cur->_data) > key){cur = cur->_right;}else{return cur;}}return nullptr;}private:Node* _root = nullptr;
};

三、map和set的封裝

????????封裝后的set?

#pragma once
#include"RBTree.h"namespace bit
{template<class K>class set{public:struct SetKeyOfT{const K& operator()(const K& key){return key;}};typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};
}

? ? ? ? ?注意這段代碼：

typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;

? ? ? ? 其中typenam是告訴編譯器這里是類型因為這里是對類模板取內嵌類型。通過set的定義我們知道set不允許被修改數值，因此我們將兩個迭代器實際上都定義為const_iterator。但是這樣定義其中insert又出問題了，因為其中的返回類型會出現不匹配的情況，即pair<iterator, bool> 和_t.Insert(key)不匹配。因為我們return返回的實際上是iterator,而實際上接受的類型為const_iterator。這時我們上面提到的用pair構造了一個新的pair而不是拷貝構造了一個pair就起到作用了，他使得返回的類型匹配！

? ? ? ? 當然我們也有其他的解決辦法：定義一個迭代器的拷貝構造?

????????STL庫中的普通迭代器都可以轉換為const迭代器，這是迭代器類的拷貝構造所支持的。

? ? ? ? ????????如下：

struct __TreeIterator
{typedef RedBlackTreeNode<T> Node;Node* _node;typedef __TreeIterator<T,Ref,Ptr> Self;typedef __TreeIterator<T, T&, T*> iterator;__TreeIterator(const iterator& it):_node(it._node){}__TreeIterator(Node* node):_node(node){}
}

?????????

? ? ? ? 封裝后的map?

????????想較于set，map的key值不可修改，但是value是可以修改的，對于他的迭代器定義按照正常的const和非const就好，但是他主要做文章的地方是在RBTree<K, pair<const K, V>, MapKeyOfT> _t;中，直接將K定義為const K了。??

#pragma once
#include"RBTree.h"namespace bit
{template<class K, class V>class map{public:struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};// 對類模板取內嵌類型，加typename告訴編譯器這里是類型typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end()const{return _t.end();}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};
}

?四、完整代碼

? ? ? ? ?RBTree.h

#pragma once// set ->key
// map ->key/valueenum Colour
{RED,BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}
};template<class T, class Ref, class Ptr>
struct __TreeIterator
{typedef RBTreeNode<T> Node;typedef __TreeIterator<T, Ref, Ptr> Self;Node* _node;__TreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}Self& operator--(){if (_node->_left){Node* cur = _node->_left;while (cur->_right){cur = cur->_right;}_node = cur;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator++(){if (_node->_right){// 下一個就是右子樹的最左節點Node* cur = _node->_right;while (cur->_left){cur = cur->_left;}_node = cur;}else{// 左子樹 根 右子樹// 右為空，找孩子是父親左的那個祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}
};// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, T>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __TreeIterator<T, T&, T*> iterator;typedef __TreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}// 新增節點給紅色cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//     g//   p   u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上更新處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 單旋//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 雙旋//     g//   p//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else  // parent == grandfather->_right{//     g//   u   p //          c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 變色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上處理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p //     c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}// 根節點->當前節點這條路徑的黑色節點的數量bool Check(Node* root, int blacknum, const int refVal){if (root == nullptr){//cout << balcknum << endl;if (blacknum != refVal){cout << "存在黑色節點數量不相等的路徑" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "有連續的紅色節點" << endl;return false;}if (root->_col == BLACK){++blacknum;}return Check(root->_left, blacknum, refVal)&& Check(root->_right, blacknum, refVal);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;//參考值int refVal = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refVal;}cur = cur->_left;}int blacknum = 0;return Check(_root, blacknum, refVal);}int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}size_t Size(){return _Size(_root);}size_t _Size(Node* root){if (root == NULL)return 0;return _Size(root->_left)+ _Size(root->_right) + 1;}Node * Find(const K & key){Node* cur = _root;KeyOfT kot;while (cur!= nullptr){	if (kot(cur->_data) < key){cur = cur->_left;}else if (kot(cur->_data) > key){cur = cur->_right;}else{return cur;}}return nullptr;}private:Node* _root = nullptr;
};

? ? ? ? myset.h?

pragma once
#include"RBTree.h"namespace bit
{template<class K>class set{public:struct SetKeyOfT{const K& operator()(const K& key){return key;}};typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};
}

? ? ? ? mymap.h

#pragma once
#include"RBTree.h"namespace bit
{template<class K, class V>class map{public:struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};// 對類模板取內嵌類型，加typename告訴編譯器這里是類型typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end()const{return _t.end();}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};
}

---

??????????????????????????感謝你耐心的看到這里?( ′･?･` )比心，如有哪里有錯誤請踢一腳作者o(╥﹏╥)o！?

????????????????????????????????? ? ? ?

?????????????????????????????????????????????????????????????????????????給個三連再走嘛~??