C++數據結構：B樹

一.?常見的搜索結構

二. B樹的概念

三. B樹節點的插入和遍歷

3.1?插入B樹節點

3.2 B樹遍歷

四. B+樹和B*樹

4.1 B+樹

4.2 B*樹

五. B樹索引原理

5.1?索引概述

5.2 MyISAM

5.3 InnoDB

六.?總結

一.?常見的搜索結構

表示1為在實際軟件開發項目中，常用的查找結構和方法，包括順序查找、二分查找、二叉搜索樹、平衡二叉樹、哈希表等，這幾種查找方法和數據結構，都適合于內查找（將數據加載到內存中查找）。

搜索結構	數據要求	時間復雜度
順序查找	無要求	O(N)
二分查找	順序排序	O(logN)
二叉搜索樹	無要求	O(N)
平衡二叉樹	無要求	O(logN)
哈希表	無要求	O(1)

如果數據量極大，內存無法存放時，就需要將數據存儲在磁盤當中，而CPU訪問磁盤的速度要遠遠低于訪問內存的速度，假設O(1)的時間復雜度下要執行2次訪問，O(logN)的時間復雜度下要執行30次訪問。如果對內存數據進行訪問，因為訪問內存速度相對較快，所有我們可以認為O(1)和O(logN)時間復雜度算法的性能是一致的。但是如果是對于磁盤上的數據的訪問，由于磁盤數據訪問的效率較低，因此O(1)和O(logN)差別會很大。

采用二叉搜索樹檢索磁盤數據的缺陷為：

二叉搜索樹查找的時間復雜度為O(logN)，磁盤IO效率低，O(logN)的時間復雜度相對于O(1)會很大程度上降低性能。

但是，哈希查找的時間復雜度是O(1)，為什么哈希也不適用于對磁盤數據的檢索呢？這是因為哈希的有這樣的缺陷：

在極端情況下，哈希表中會產生大量的哈希沖突，查找的時間復雜度會接近O(N)。
雖然很多時候當哈希沖突達到一定數量時，在哈希散列中會由掛單鏈表改為掛紅黑樹，但紅黑樹查找的時間復雜度依舊是O(logN)。

為了解決平衡二叉樹和哈希表無法很好的應對內存數據查找的情況，B樹被創造和出來，B樹適用于對磁盤中大量的數據進行檢索，當然B樹也能夠在內存在查找數據，但效果就不如哈希和平衡二叉樹。

由于B樹/B+樹適用于檢索磁盤中大量數據的性質，經常被用于作為數據庫的底層檢索結構。

二. B樹的概念

B樹是一種適合外查找的平衡多叉樹，一顆m階的B樹，是一顆m路的二叉搜索樹，一顆B樹要么為空樹，要么滿足如下幾個條件：

根節點至少有兩個孩子節點。
分支節點（非葉子節點）應當有K-1個鍵值和K個孩子節點，其中 $ceil(m/2)\leqslant K\leqslant M$ ，其中ceil為向上取整函數。
所有葉子節點都在同一層。
每個節點中的鍵值都是自小到大升序排序的，鍵值Key表示子樹的閾值劃分。
對于任意一個節點，孩子節點的數目總是比鍵值多一個。

圖2.1就是一顆3階B樹，注意觀察其根節點，兩個鍵值為50和100，根節點的第一個孩子節點鍵值全部小于50，第二個孩子節點的鍵值位于(51,100)之間，第三個孩子節點鍵值大于100，這就是鍵值Key的閾值劃分功能。

B樹檢索與二叉搜索樹的檢索類似，假設我們要在圖2.1所示的B樹中檢索99，先從根節點開始找起，對比待查找的值和鍵值的大小，發現其位于(50,100)范圍內，這樣就向下遍歷查找p2子樹，在p2子樹的鍵值中找到了鍵值99，檢索完成。

三. B樹節點的插入和遍歷

3.1?插入B樹節點

由于B樹的插入操作過于抽象，因此直接上實例，在示例中講解B樹節點插入的具體操作。假設依次將std::vector<int> v = { 53,139,75,49,145,36,50,47,101}插入到3階B樹中。為了方便插入操作，我們在申請B樹節點空間的時候，階數為M，就為鍵值申請M個空間，為孩子節點申請M+1個空間，這樣做的目的是方便插入時數據挪動，以及后面的分裂操作。

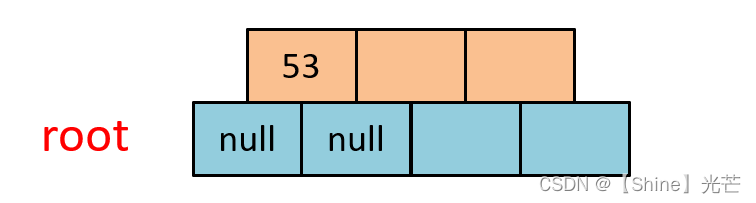
① 插入53

53是B樹插入的第一個節點，因此直接將其插入到根節點的第一個鍵值位置處即可。如果3.1所示，插入53后，有一個B樹根節點，這個根節點附帶有兩個孩子節點nullptr。這里的根節點也是葉子節點，注意B樹插入新節點一定是向葉子節點插入的。

②?插入139

139大于53，且插入后根節點（葉子結點）中鍵值的數目不超過M-1，因此只需將139至于53的后面，并且帶入null子節點即可。

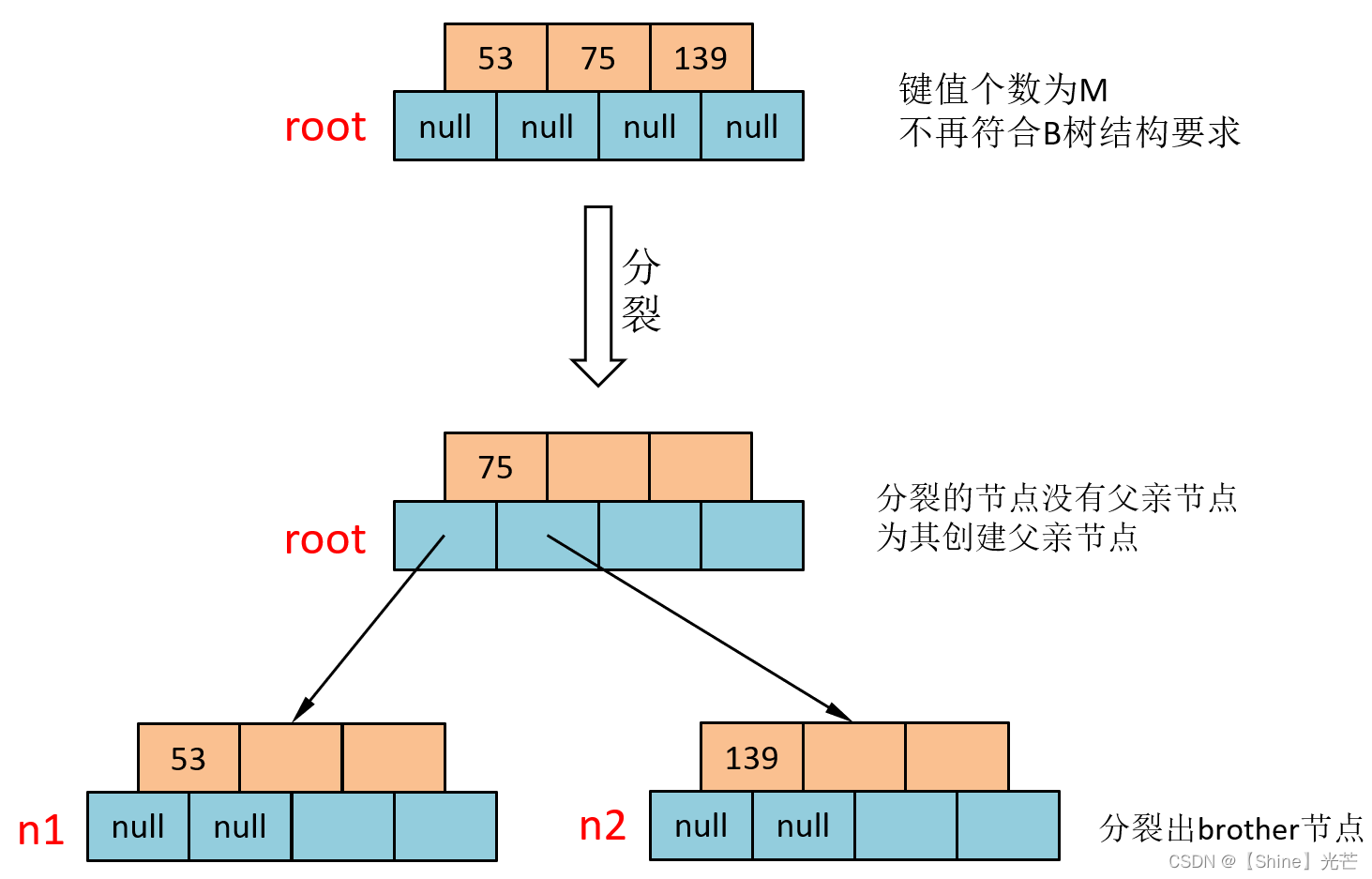
③ 插入75

75位于53和139之間，所以第一步要現將75插入到root節點的這兩個值之間。但是，插入75后root節點就有了3個鍵值，這樣就不符合B樹的結構要求，需要進行分裂。

分裂操作的步驟為：

取中間位置mid = M/2下標處為分界線，創建一個兄弟節點brother，將下標位于[mid+1,M)的鍵值及其左右孩子都拷貝到brother節點中去（設下標為鍵值相同的孩子節點為左孩子，比鍵值下標大1的孩子節點稱為右孩子）。
將mid處的鍵值交給其父親節點，如果沒有父親節點節創建父親節點，父親節點的其中兩個孩子節點就包含原先發生分裂的節點以及分裂出的節點brother。

④?插入49

首先檢索節點插入的位置，發現49小于根節點root的第一個鍵值，因此找到n1節點，n1節點為葉子節點可以執行插入操作，49小于第一個節點53，所以應當將53向后移動一位并將49設置為n1節點的第一個鍵值。

?⑤?插入145

首先檢索插入數據的葉子節點，根節點只有一個鍵值75，145大于75，向n2節點查找，n2為葉子節點可以執行插入操作，將145插入到139后面，插入過后鍵值個數少于階數M，不用分裂。

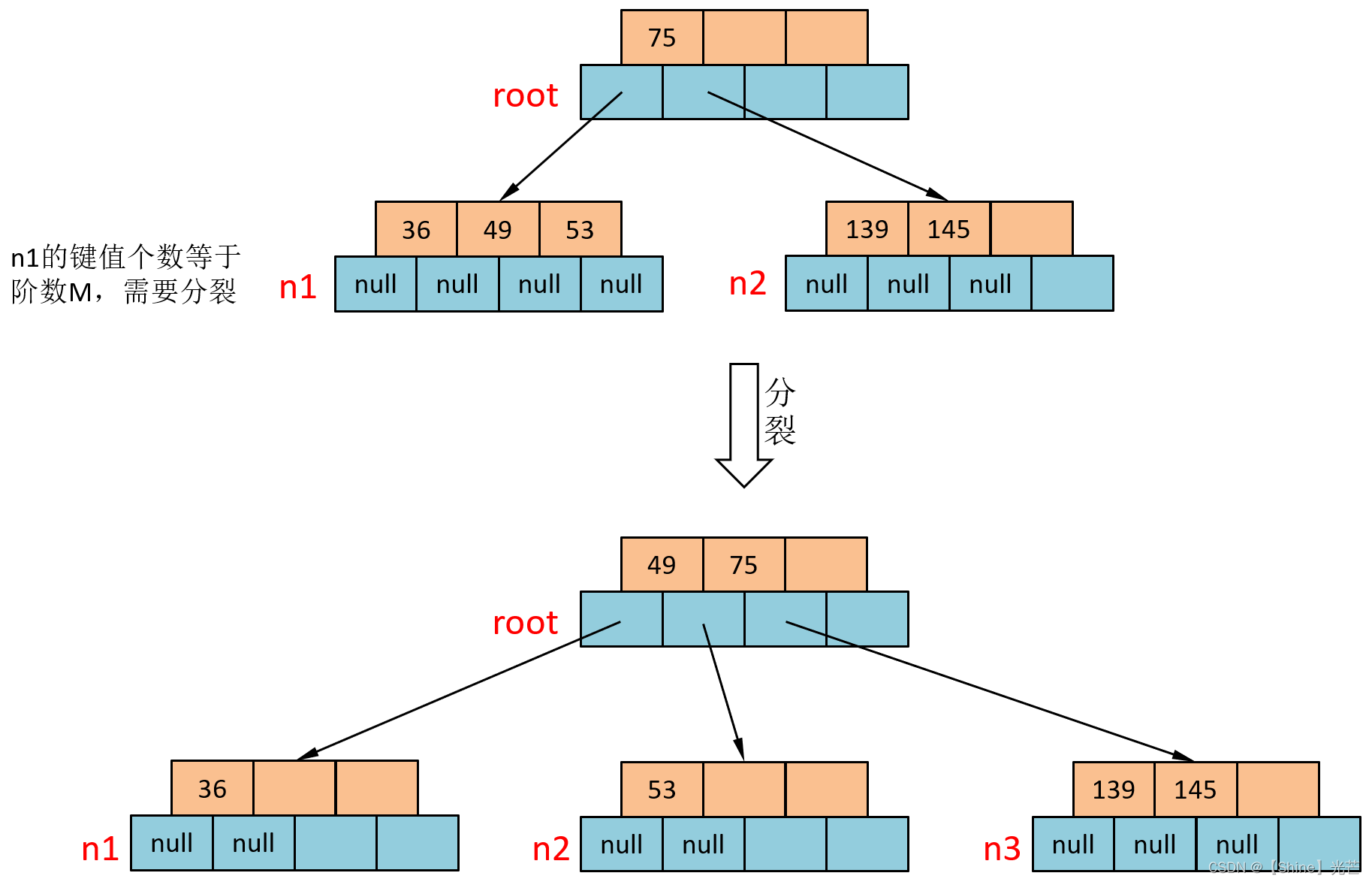
⑥?插入36

查找36的插入位置應該為圖3.5中的n1節點，將35插入n1后n1有3個鍵值需要進行分裂，兄弟節點取走53，49向上交給n1的父親節點，分裂出的兄弟節點要作為root節點的一個孩子節點。

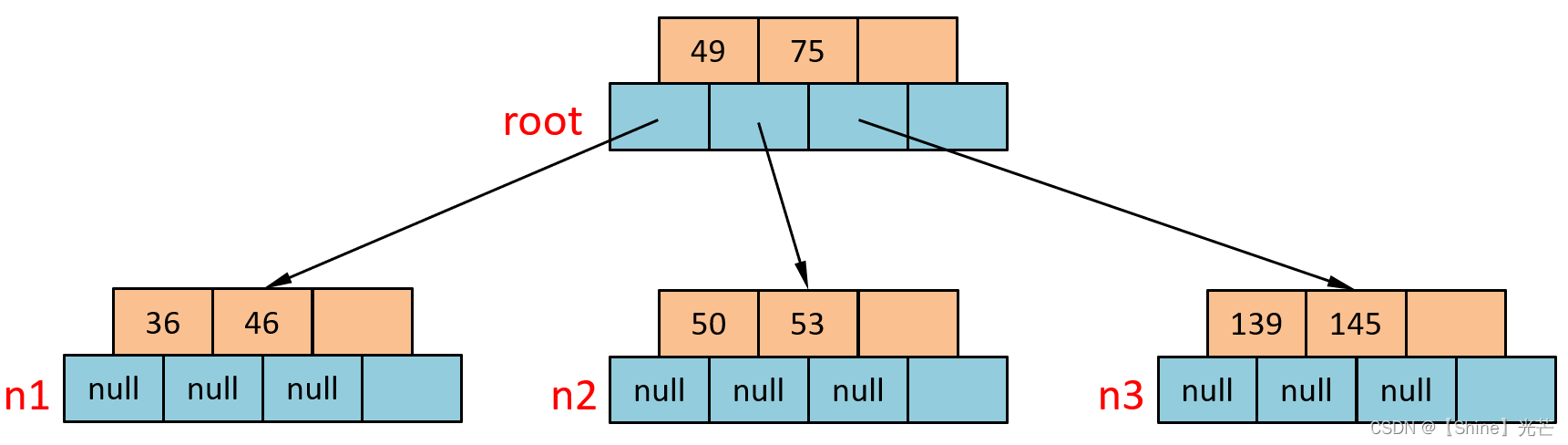
⑦?插入50?

直接找到n2節點，插入到鍵值53之前即可。

⑧?插入47

?插入到n1節點46的后面即可。

⑨?插入101

先初步執行插入操作，即101插入到n3節點的第一個鍵值位置處，插入后n3節點的鍵值數量達到了階數M，要執行分裂操作。然而分裂后將mid處鍵值交給父親節點（root）管理后，root的鍵值數量也達到了階數M，需要進一步分裂，更新root。

3.2 B樹遍歷

B樹是一種特殊的搜索樹，如果按照中選遍歷，那么理應得到升序的一組數據，B樹遍歷的方法與普通的二叉搜索樹中序遍歷并沒有本質區別，區別在于M路遍歷和雙路遍歷。圖3.10為二叉搜索樹的遍歷流程圖，遍歷得到升序排序結果。

代碼3.1：插入B樹節點和前序遍歷B樹

#include <iostream>// B樹節點，K為索引數據類型，M為最大階數
template<class K, size_t M>
struct BTreeNode
{// 存儲鍵值和孩子節點的一維數組// K _key[M - 1];// BTreeNode<K, M> _sub[M];// 為了方便后續的分裂和插入操作，多開辟一個空間K _key[M];BTreeNode<K, M>* _sub[M + 1];BTreeNode<K, M>* _parent;   // 父親節點size_t _n;   // 鍵值個數// 構造函數BTreeNode(): _parent(nullptr), _n(0){// 鍵值全部清零，孩子節點全部為空for (size_t i = 0; i < M; ++i){_key[i] = K();_sub[i] = nullptr;}_sub[M] = nullptr;}
};template<class K, size_t M>
class BTree
{typedef BTreeNode<K, M> Node;   // B樹節點類型重定義
public:// 插入位置查找函數std::pair<Node*, int> Find(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){// 在本層中，查找大于key的鍵值，如果找到這樣的鍵值或者走到了最后一個鍵值// 那么就到下一層去查找，如果找到與key相同的鍵值，那么就直接返回該位置對應pairsize_t i = 0;while (i < cur->_n){// 鍵值按照升序排序，逐個向后查找即可if (key > cur->_key[i]) {++i;}else if (key < cur->_key[i]){break;}else   // 存在相等就直接返回{return std::make_pair(cur, i);}}parent = cur;cur = cur->_sub[i];}return std::make_pair(parent, -1);}// 在一個B樹節點值插入新鍵值的函數void InsertKey(Node* parent, const K& key, Node* child){int end = parent->_n - 1;while (end >= 0){if (parent->_key[end] > key){// 將大于key的鍵值及其對應的右孩子節點全部向后移動一位parent->_key[end + 1] = parent->_key[end];parent->_sub[end + 2] = parent->_sub[end + 1];--end;}else{break;}}// 將新的key值插入到end+1位置處，并引入右孩子節點parent->_key[end + 1] = key;parent->_sub[end + 2] = child;++parent->_n;}// 新節點（鍵值）插入函數bool Insert(const K& key){// 特殊情況：當前B樹根節點為空，插入的是第一個節點if (_root == nullptr){_root = new Node;_root->_key[0] = key;_root->_n++;return true;}// 查找要插入節點的位置std::pair<Node*, int> ret = Find(key);// 如果對應ret.second>=0，那說明key已經在B樹中存在// B樹不允許冗余，因此直接返回falseif (ret.second >= 0){return false;}Node* parent = ret.first;Node* child = nullptr;K newKey = key;// 向上插入，滿足條件就分裂while (true){InsertKey(parent, newKey, child);if (parent->_n <= M - 1){return true;}else   // 需要進行分裂操作{size_t mid = M / 2;   // 中間節點// 將中間mid之后的鍵值全部交給新創建的brother節點Node* brother = new Node;size_t j = 0;for (size_t i = mid + 1; i < M; ++i){// 將key及其左孩子交給brother節點brother->_key[j] = parent->_key[i];brother->_sub[j] = parent->_sub[i];// 如果左孩子節點不為空，那么就要跟新其父親為brotherif (parent->_sub[i] != nullptr){parent->_sub[i]->_parent = brother;}// 將parent節點中被挪走的key和sub清空parent->_key[i] = K();parent->_sub[i] = nullptr;++j;}// 將最后一個右孩子節點插入到brother節點中brother->_sub[j] = parent->_sub[M];if (parent->_sub[M] != nullptr){parent->_sub[M]->_parent = brother;}parent->_sub[M] = nullptr;// 更新鍵值個數，這里parent鍵值個數減去brother->_n + 1，+1是因為要把mid子節點交給父節點brother->_n = j;parent->_n -= (brother->_n + 1);K midKey = parent->_key[mid];parent->_key[mid] = K();if (parent == _root){_root = new Node;_root->_key[0] = midKey;_root->_sub[0] = parent;_root->_sub[1] = brother;parent->_parent = _root;brother->_parent = _root;_root->_n++;return true;}else{newKey = midKey;parent = parent->_parent;brother->_parent = parent;child = brother;}}}return true;}void _InOrder(Node* root){if (root == nullptr){return;}// 依次遍歷每個節點的左孩子for (size_t i = 0; i < root->_n; ++i){_InOrder(root->_sub[i]);std::cout << root->_key[i] << " ";}// 遍歷最后一個右孩子節點_InOrder(root->_sub[root->_n]);}// 中序函數void InOrder(){// 子函數_InOrder(_root);}private:Node* _root = nullptr;
};

四. B+樹和B*樹

4.1 B+樹

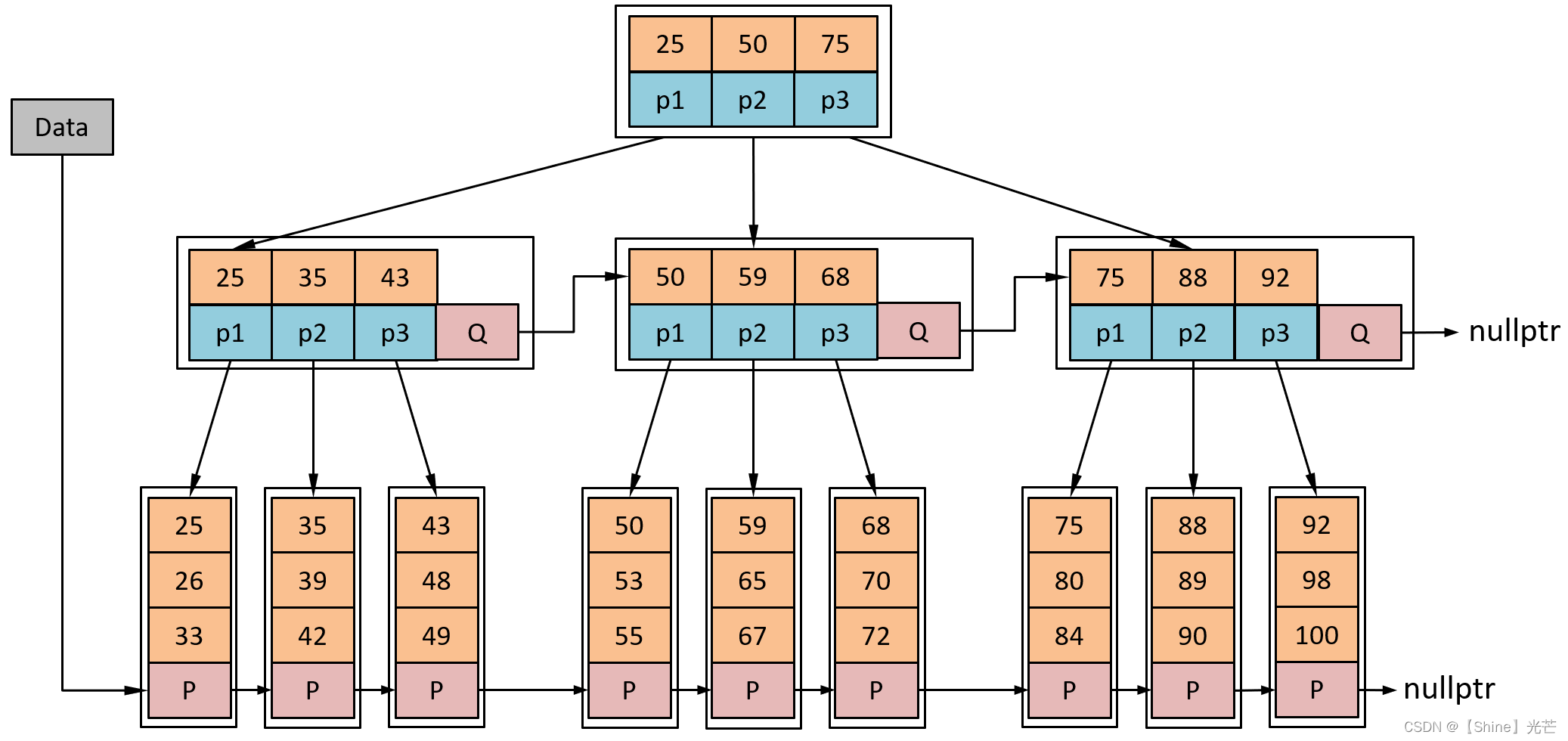
B+樹是在B樹上優化了的多路平衡搜索二叉樹，相比于B樹，B+樹進行了以下幾點優化：

每個節點的鍵值數量和孩子節點數量相同。
孩子節點指針p[i]指向的子B樹鍵值范圍位于 [ k[i], k[i+1] ) 之間。
所有存儲了有效鍵值的節點都在葉子節點上。
所有葉子節點都被連接了起來。

B+樹的節點插入，與B樹類似，同樣由于其過于抽象，本文以具體的實例來展示B+樹節點插入的過程，假設要將std::vector<int> v = { 53,139,75,49,145,36,101 }插入到階數M=3的B+樹中去，插入的流程及操作如下：

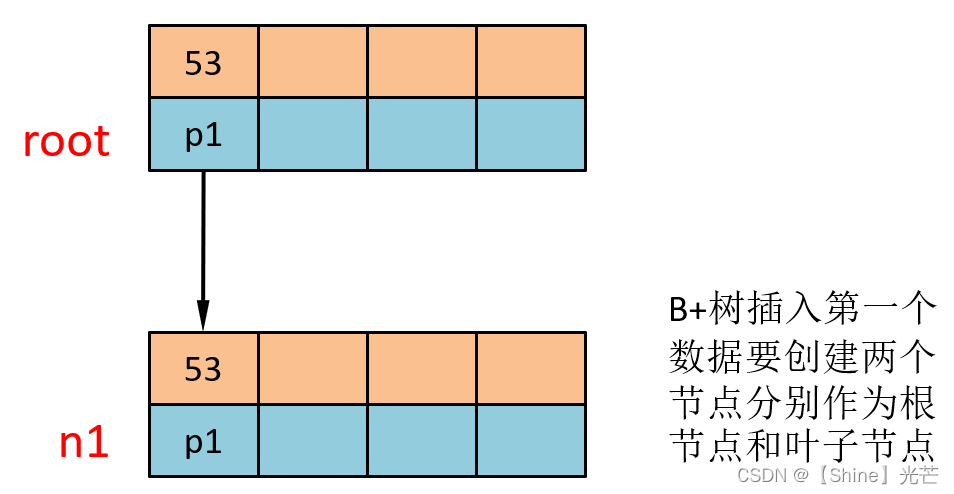
①?插入53

插入的第一個節點，首先創建兩層B+樹節點，一層為根節點，一層為葉子節點，在根節點和葉子節點的第一個鍵值位置處，插入元素53。和B樹一樣，如果階數為M，就為鍵值和孩子節點都多開辟一個空間，以方便數據挪到和節點分裂。

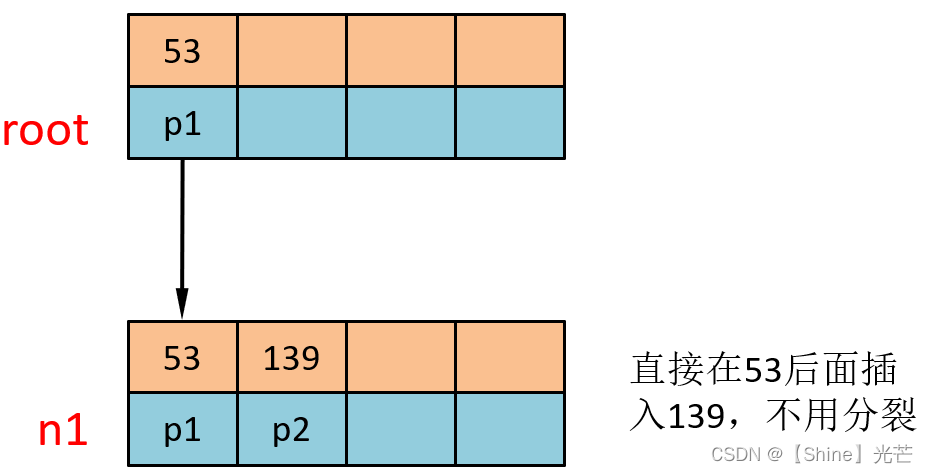
②?插入139

首先檢索插入位置，發現139大于根節點中唯一一個鍵值53，因此向下遍歷找到n1，將新數據插入到53后面，節點中鍵值個數尚未達到階數，不需要分裂。

③?插入75

檢索到75應該插入子節點n1中，139向后挪一個單位，75插入到53和139之間，以保證鍵值升序。

④?插入49

首先查找可以插入49的葉子節點，檢索到插入位置為第一個鍵值位置，因此要更新其父親節點中對應位置的索引值，這樣root的第一個鍵值就由53變為了49。同時，由于n1中的鍵值個數已經超過了階數M，所以要對這個節點執行分裂操作。

B+樹節點分裂操作：

創建兄弟節點brother，將分裂節點中后半部分鍵值挪動到brother中。
并將brother中首個鍵值插入到父親節點中，將brother節點設為父節點的孩子節點。

⑤?插入145

直接將145插入到節點n2中去，因為插入后鍵值數量未超過B樹的階數，不需要分裂。

⑥?插入36

將36插入到n1的首個位置處，然后更新器父親節點對應的鍵值。（B+樹中向葉子節點的首個關鍵字位置插入數據，一定會更新父親節點的索引）

⑦?插入101

將101插入到n2的鍵值75和39之間，然后n2分裂。

4.2 B*樹

相比于B+樹，B*樹要求每個分支節點的鍵值利用率達到 $\frac{2}{3}M$ ，并且每一層節點又要存儲指向其兄弟節點的指針，B*樹相對于B+樹，最大的優化就是節省了空間，能減少空間浪費。

五. B樹索引原理

5.1?索引概述

索引，就是通過某些關鍵信息，讓用戶可以快速找到某些事物，例如通過目錄，我們就可以快速檢索到一本書中特定的內容所在的頁碼。B/B+最普遍的用途，就是做索引。

MySQL數據庫官方給出的索引定義是：索引（index）是幫助MySQL高效獲取數據的數據結構。

當數據量很大的時候，為了方便數據的管理、提高檢索效率，通常會將數據保存至數據庫。數據庫不僅僅要存儲數據，還要維護特定的數據結構和一些高效的搜索算法，以幫助用戶快速引用到某些數據。這種實現快速查找的數據結構，就是索引。

MySQL是非常流行的開源關系型數據庫，不僅免費，而且搜索效率較高，可靠性高，擁有靈活的插件式存儲引擎，在MySQL中，索引是屬于存儲引擎范疇的概念，不同的存儲引擎對索引的實現方式是不同的。索引是基于表的而不是基于數據庫的。

5.2 MyISAM

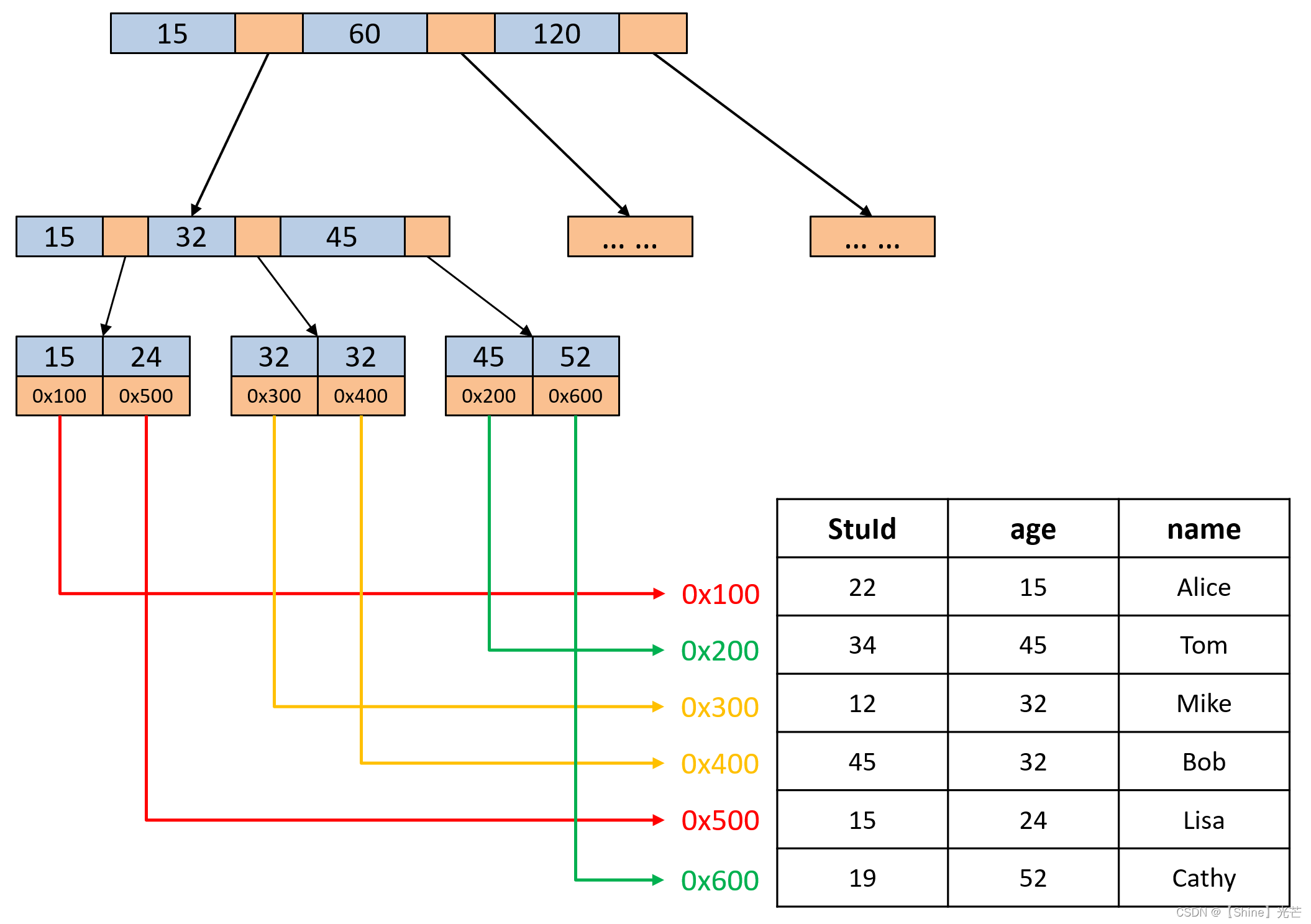
在早期的MySQL數據庫中，所使用的搜索引擎都是MyISAM，這種搜索引擎不支持事務，支持全文索引，其使用的數據結構是B+樹。在MyISAM搜索引擎中，葉子節點中的data域存儲的是數據在磁盤中的地址，而不是數據本身。如圖5.1所示的學生信息管理數據庫，要記錄學生的學號(StuId)、年齡(age)以及姓名，B+樹用于檢索，圖5.1中選取的主鍵為StuId。

在絕大部分數據庫中，一般要求加入到數據庫中的數據要有一個主鍵，并且主鍵是不允許出現重復的。就以圖5.1所示的學生信息管理系統為例，選取學號能保證每個學生之間的學號不重復，而姓名和年齡則不可避免的出現重復，那么就應當選取學號作為主鍵。如果沒有一個合適的參數作為主鍵，那么可以采用自增主鍵，自增主鍵實際就是一個常數，第一次插入的數據常數1為主鍵，第二次插入的數據常數2為主鍵，以此類推。

以圖如果用戶通過主鍵索引查找數據庫中的相關信息，那么就會對B樹進行檢索，直到檢索到葉子節點發現匹配項或者確認數據庫中沒有對應主鍵即可。如果使用非主鍵（未建立輔助索引）的參數進行檢索，那么進行的操作是全表掃描查找匹配項。

對于MySQL數據庫，我們處理使用主鍵建立主索引之外，還可以建立輔助索引，主索引不允許出現重復項，而輔助索引允許出現重復項，如圖5.2所示，就是通過學生年齡age建立的學生數據庫的輔助索引。

5.3 InnoDB

現在高版本的MySQL數據庫，全部采用InnoDB為搜索引擎，InnoDB是面向在線事務處理的應用，支持B+樹索引、哈希索引、全文索引等。但是，InnoDB使用B+樹支持索引的實現方式與MyISAM卻有著很大的不同。

InnoDB文件本身就是索引文件的一部分。在InnoDB的中，B+樹的葉子節點要存放表的全部數據，數據庫中的數據，要按照主鍵從小到大的順序排列起來。如圖5.3所示，InnoDB的葉子節點中要包含所有的數據記錄，這種索引叫做聚集索引。由于InnoDB數據文件本身要按照主鍵來聚集，因此InnoDB必須有主鍵，而MyISAM則可以沒有主鍵。

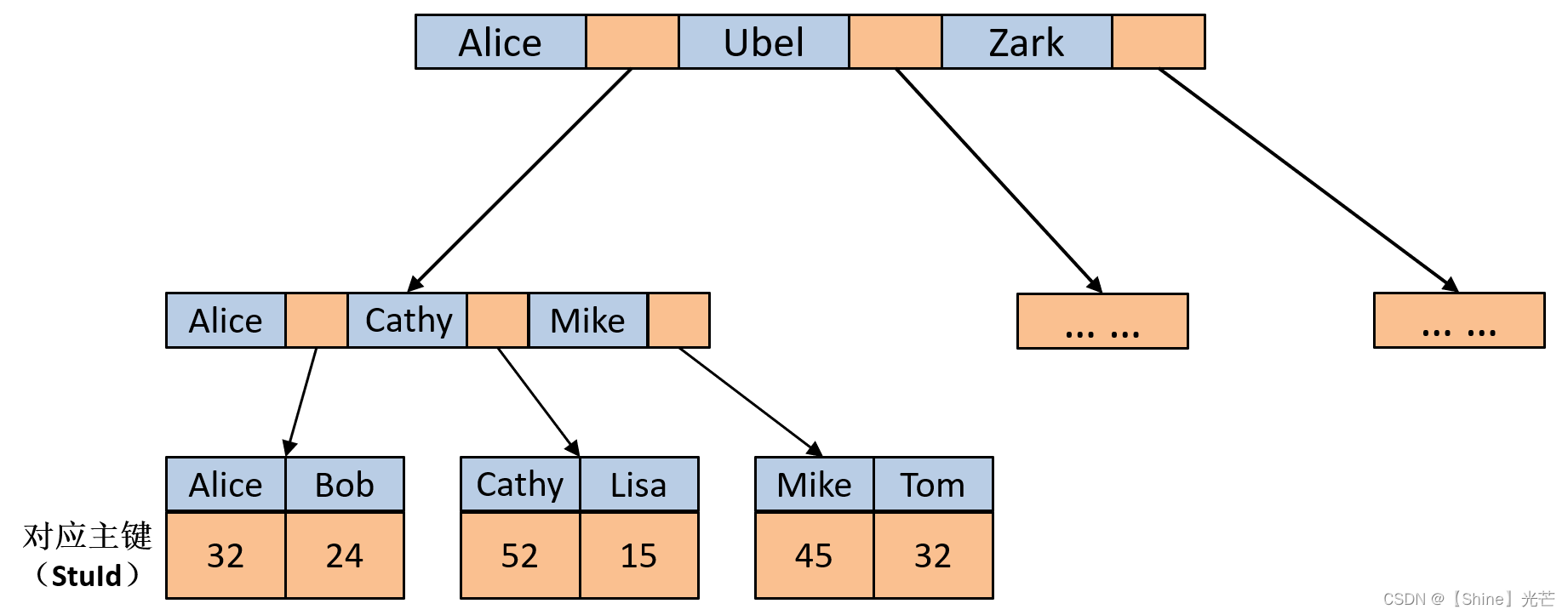
InnoDB建立B+樹輔助索引，葉子節點的數據域中記錄的并不是數據數據文件本身的內容，而是對應的主鍵，如圖5.4所示，在InnoDB索引方式下，建立對于name的輔助索引，葉子結點數據域就存儲了對應的StdId（學號），使用輔助索引檢索時，先拿到對應的主鍵，再通過主索引查找內容，這樣就相當于要檢索兩次。

六.?總結

常見的搜索結構有哈希、二分、順序查找、平衡二叉樹等，這些數據結構和算法都只適用于內查找。
對于海量數據，內存中無法容納，應當使用B樹/B+樹來進行檢索，B/B+樹是高效的外查找專用數據結構。
MySQL數據庫的檢索主要是通過B+樹來進行的，有MyISAM和InnoDB兩種檢索方式，MyISAM的B+樹的葉子節點的數據域中存儲的是數據文件在磁盤中的地址，InnoDB的B+樹的葉子節點中數據域存放的是數據文件本身。
B+樹做外查找時，B+樹本身存儲在磁盤中。