機器學習--稀疏學習

前置知識：

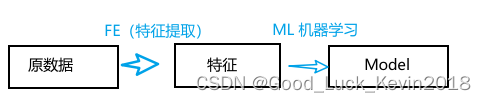
通常學習一次模型的過程如下：我們普遍為了獲取更好的模型效果，直接對原始數據學習，會造成過擬合、需要特征提取；

而若特征提取完后依舊有很多特征，還是會容易過擬合。這時候就需要特征降維和特征選擇。

其中：

特征降維：相當于將高維數據映射到低維空間（會改變數據的表示，低維空間映射后的特征不容易解釋）

特征選擇：根據特征的重要權重，不會改變維度，單純提取部分更合適的特征來使用。（是一種舍棄不重要特征）

特征：

有關特征：對學習任務有用的特征（保留）；

無關特征：對學習任務無用的特征（舍棄）；

特征選擇目的：

1. 減輕特征災難，2. 降低學習難度

特征選擇的常用方法：

1. 前向搜索：先確定一個特征集合和最優子集，依次從特征集合中選出最優特征，將最優特征移入最優子集，迭代此過程直到當前特征不再優于上一輪最優子集結束。

2. 后向搜索：先將整個特征集合作為候選子集，依次去除不相關特征；直到當特征子集不再優于上輪子集結束。

3.?雙向搜索：前向和后向結合；在每輪迭代中，一次選出最優和最差特征，將最優特征移入最優子集，最差特征從候選子集去掉。

子集評價

核心：屬性子集的信息增益：

當我們不斷的往最優子集追加特征時，我們需要不斷的計算是否帶來了信息增益：

例如：我們判斷一個人成績是否合格，當沒有任何特征時，是最混亂的，我們無從猜測。（也就是Ent(D)信息熵值最大），當我們引入了他對這門課程的累計投入學習時長（特征）時，我們就有了一定的了解（降低了我們的混亂程度）。隨著不斷的引入其他特征，我們愈發的能更大概率的確認該學生是否成績合格。

其中：D^v是特征子集，|D|是權重。Ent(D)是當前子集劃分下的信息熵；?Gain(A)是信息增益。v是特征子集對結果的劃分集合；

特征選擇

過濾式

過濾式方法是一種將特征選擇與學習器訓練相分離的特征選擇技術。

????????1）、先將相關特征挑選出來;

????????2）、再使用選擇出的數據子集來訓練學習器。

選擇--Relief算法：

為解決二分類問題

算法思想：

????????使用一個“相關統計量”來度量特征的重要性，該統計量是一個向量，其中每個分量代表著相應特征的重要性，因此我們最終可以根據這個統計量各個分量的大小來選擇出合適的特征子集。

????????對于數據集中的每個樣例xi，首先找出與xi同類別的最近鄰與不同類別的最近鄰，分別稱為猜中近鄰（near-hit）與猜錯近鄰（near-miss），接著便可以分別計算出相關統計量中的每個分量。對于j分量：

$\delta ^j = \sum _{i} -diff(x_i^j, x_{i,nh}^j)^2 +diff(x_i^j, x_{i,nm}^j)^2$

直觀上理解：對于猜中近鄰，兩者j特征屬性的距離越小越好，對于猜錯近鄰，j屬性距離越大越好。更一般地，若xi為離散屬性，diff取海明距離，即相同取0，不同取1；若xi為連續屬性，則diff為曼哈頓距離，即取差的絕對值，Xa在屬性j三的取值均規范化到[0,1],分別計算每個分量，最終取平均便得到了整個相關統計量。

迭代選取xi過程m次，根據 $\delta ^j$ 更新j權重，最后得到各特征的平均權重。特征值越大的分類能力越強。

算法特點：時間開銷隨采樣次數以及原始數據特征線性增長，運行效率高。

Relief-F：多分類問題

對于j分量，新的計算公式如下：

$\delta ^j = \sum _i -diff(x_i^j, x_{i,nh}^j)^2 +\sum_{l\neq k} (pl \times diff(x_i^j, x_{i,l,nm}^j)^2 )$

其中pl表示第l類樣本在數據集中所占的比例權重，易知兩者的不同之處在于：標準Relief 只有一個猜錯近鄰，而Relief-F有多個猜錯近鄰。

Relief算法只是在數據集上采樣計算，而不是針對整個訓練集估計特征權重，屬于是高效的過濾式特征選擇算法。

包裹式選擇

直接把最終將要學習的學習器的性能作為特征子集的評價準則。（將特征選擇和模型訓練融合）

包裹方法是一種為給定學習器選擇最有利于其性能的特征子集（量身定做）。

比過濾式的特征選擇效果更好。

LVW包裹式算法：拉斯維加斯框架下采用隨機策略進行子集搜索，以最終很累起的誤差為特征自己的評價準則；

	LVW拉斯維加斯方法	蒙特卡羅方法
算法思路??	1. 隨機產生特征子集； 2. 使用交叉驗證推斷當前子集誤差 3. 多次循環，選擇誤差最小的子集作為最終子集。	1. 基于概率的方式，隨機從特征池中選取一定數量特征 2. 訓練模型，得到模型的性能 3. 選取新的隨機特征，以獲取最佳特征子集。
有時間限制下	可能給出也可能不給出解	一定有解
無時間限制下	有解	有解
解的特點	采樣越多，越有機會得到最優解，有解必最優	采樣越多，解越優，不一定得出最優解
算法特點????????	訓練開銷大	容易過擬合，訓練開銷大