SCI一區級 | Matlab實現GWO-CNN-BiLSTM-selfAttention多變量多步時間序列預測

預測效果

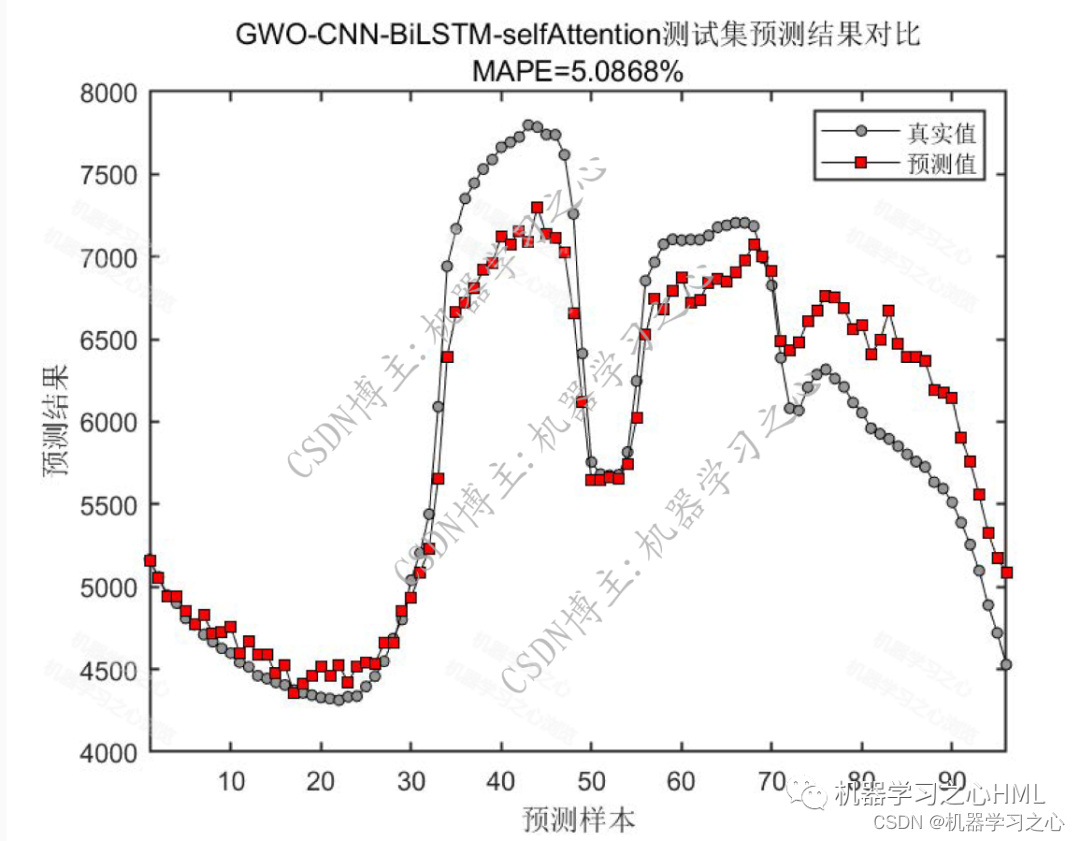
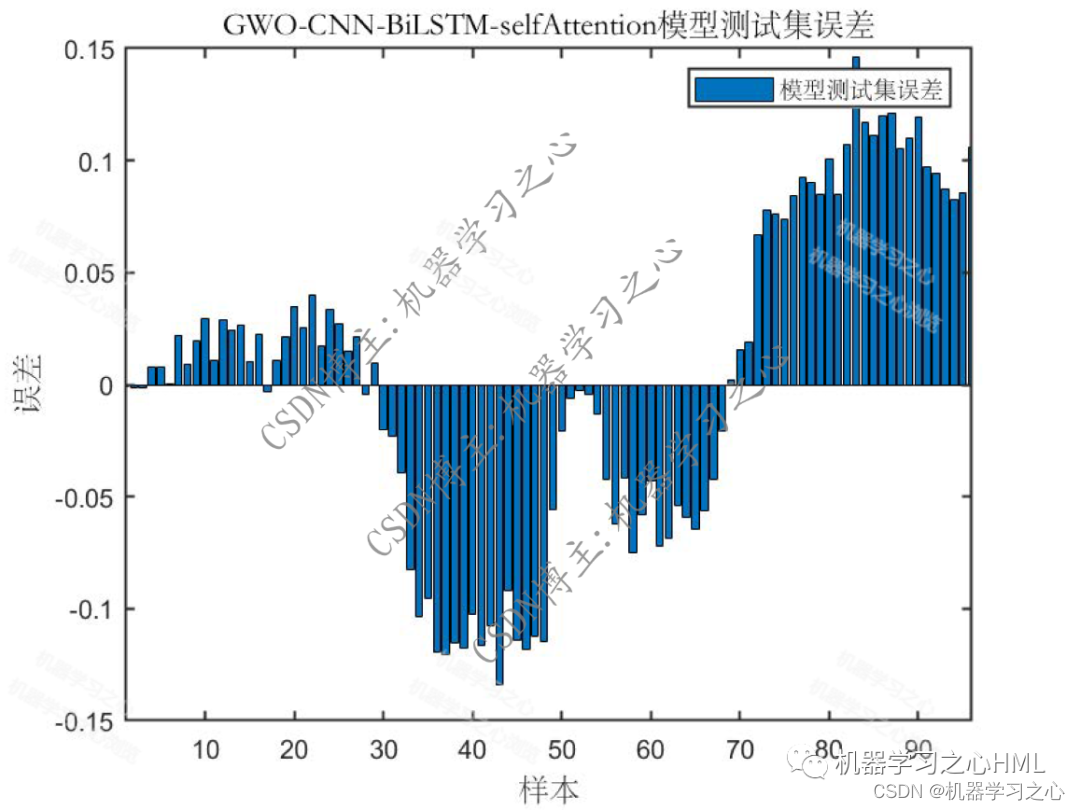
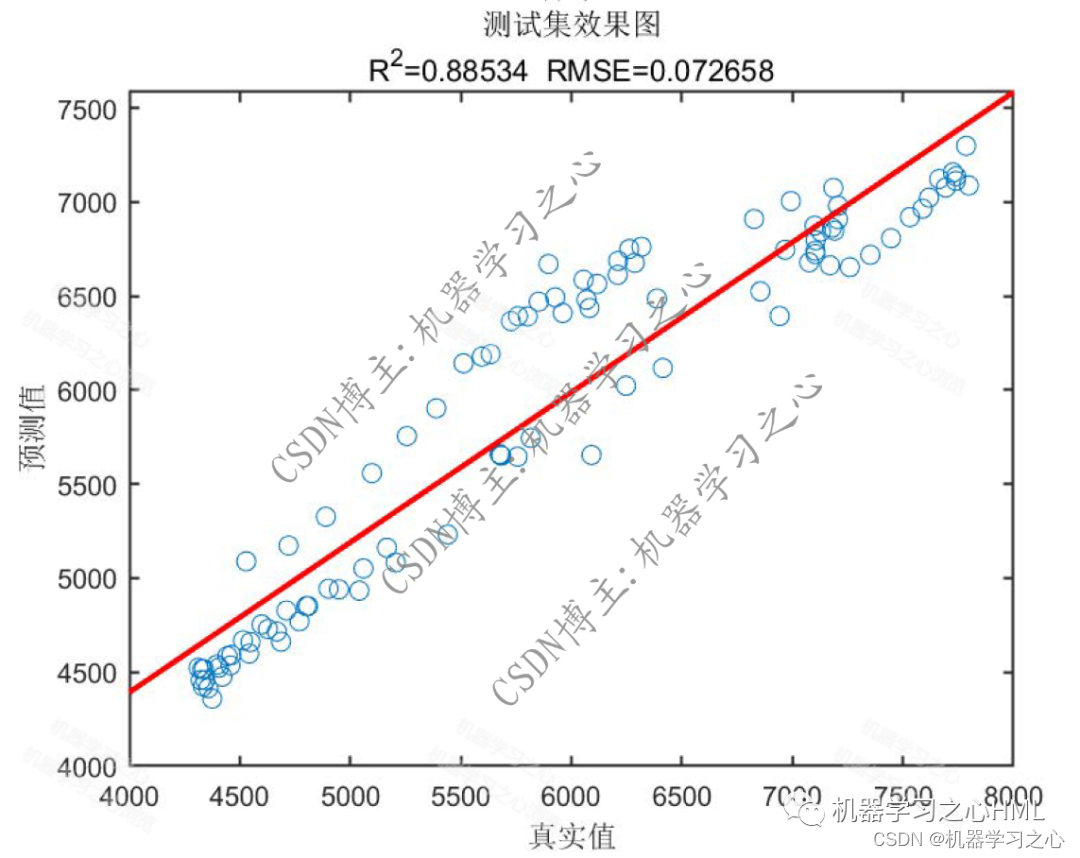
基本介紹

1.Matlab實現GWO-CNN-BiLSTM-selfAttention灰狼算法優化卷積雙向長短期記憶神經網絡融合自注意力機制多變量多步時間序列預測，灰狼算法優化學習率，卷積核大小，神經元個數，以最小MAPE為目標函數；

自注意力層 (Self-Attention)：Self-Attention自注意力機制是一種用于模型關注輸入序列中不同位置相關性的機制。它通過計算每個位置與其他位置之間的注意力權重，進而對輸入序列進行加權求和。自注意力能夠幫助模型在處理序列數據時，對不同位置的信息進行適當的加權，從而更好地捕捉序列中的關鍵信息。在時序預測任務中，自注意力機制可以用于對序列中不同時間步之間的相關性進行建模。

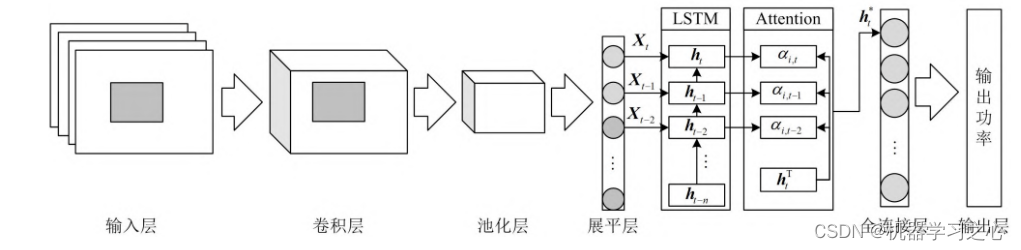
2.運行環境為Matlab2023a及以上，提供損失、RMSE迭代變化極坐標圖；網絡的特征可視化圖；測試對比圖；適應度曲線（若首輪精度最高，則適應度曲線為水平直線）；

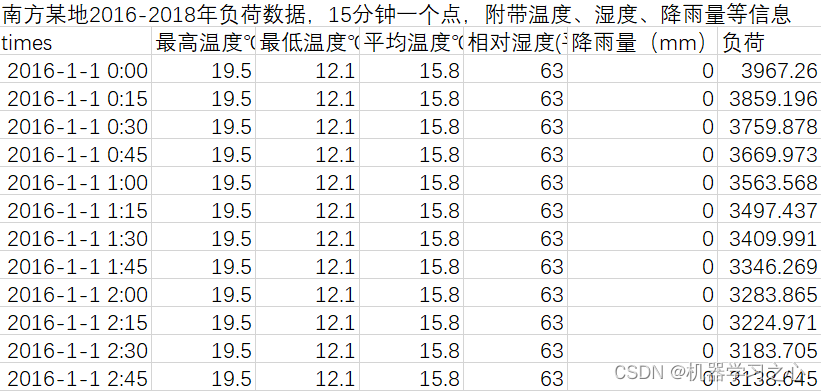
3.excel數據集（負荷數據集），輸入多個特征，輸出單個變量，考慮歷史特征的影響，多變量多步時間序列預測（多步預測即預測下一天96個時間點），main.m為主程序，運行即可，所有文件放在一個文件夾；

4.命令窗口輸出SSE、RMSE、MSE、MAE、MAPE、R2、r多指標評價；
適用領域：負荷預測、風速預測、光伏功率預測、發電功率預測、碳價預測等多種應用。

程序設計

• 完整程序和數據獲取方式：私信博主回復Matlab實現GWO-CNN-BiLSTM-selfAttention多變量多步時間序列預測獲取。

%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% Grey Wolf Optimizer
% 灰狼優化算法function [Alpha_score, Alpha_pos, Convergence_curve, bestPred,bestNet,bestInfo ] = GWO(SearchAgents_no, Max_iter, lb, ub, dim, fobj)
% 輸入參數：
% SearchAgents_no：搜索個體的數量
% Max_iter：最大迭代次數
% lb：搜索空間的下界（一個1維向量）
% ub：搜索空間的上界（一個1維向量）
% dim：問題的維度
% fobj：要優化的目標函數，輸入為一個位置向量，輸出為一個標量% 初始化alpha、beta和delta的位置向量
Alpha_pos = zeros(1, dim);
Alpha_score = inf; % 對于最小化問題，請將其改為-infBeta_pos = zeros(1, dim);
Beta_score = inf; % 對于最小化問題，請將其改為-infDelta_pos = zeros(1, dim);
Delta_score = inf; % 對于最小化問題，請將其改為-inf% 初始化領導者的位置向量和得分Positions = ceil(rand(SearchAgents_no, dim) .* (ub - lb) + lb);Convergence_curve = zeros(1, Max_iter);l = 0; % 迭代計數器% 主循環
while l < Max_iterfor i = 1:size(Positions, 1)% 將超出搜索空間邊界的搜索代理放回搜索空間內Flag4ub = Positions(i, :) > ub;Flag4lb = Positions(i, :) < lb;Positions(i, :) = (Positions(i, :) .* (~(Flag4ub + Flag4lb))) + ub .* Flag4ub + lb .* Flag4lb;% 計算每個搜索個體的目標函數值[fitness,Value,Net,Info] = fobj(Positions(i, :));% 更新Alpha、Beta和Delta的位置向量if fitness < Alpha_scoreAlpha_score = fitness;       % 更新Alpha的得分Alpha_pos = Positions(i, :); % 更新Alpha的位置向量bestPred = Value;bestNet = Net;bestInfo = Info;endif fitness > Alpha_score && fitness < Beta_scoreBeta_score = fitness;       % 更新Beta的得分Beta_pos = Positions(i, :); % 更新Beta的位置向量endif fitness > Alpha_score && fitness > Beta_score && fitness < Delta_scoreDelta_score = fitness;       % 更新Delta的得分Delta_pos = Positions(i, :); % 更新Delta的位置向量endenda = 2 - l * ((2) / Max_iter); % a從2線性減少到0% 更新搜索個體的位置向量for i = 1:size(Positions, 1)for j = 1:size(Positions, 2)r1 = rand(); % r1是[0,1]區間的隨機數r2 = rand(); % r2是[0,1]區間的隨機數A1 = 2 * a * r1 - a; % 參考文獻中的公式(3.3)C1 = 2 * r2; % 參考文獻中的公式(3.4)D_alpha = abs(C1 * Alpha_pos(j) - Positions(i, j)); % 參考文獻中的公式(3.5)-part 1X1 = Alpha_pos(j) - A1 * D_alpha; % 參考文獻中的公式(3.6)-part 1r1 = rand();r2 = rand();

參考資料

[1] http://t.csdn.cn/pCWSp
[2] https://download.csdn.net/download/kjm13182345320/87568090?spm=1001.2014.3001.5501
[3] https://blog.csdn.net/kjm13182345320/article/details/129433463?spm=1001.2014.3001.5501