題目描述
給定一個二叉樹的 根節點 root,想象自己站在它的右側,按照從頂部到底部的順序,返回從右側所能看到的節點值。
示例 1:
輸入:root = [1,2,3,null,5,null,4]
輸出:[1,3,4]
解釋:
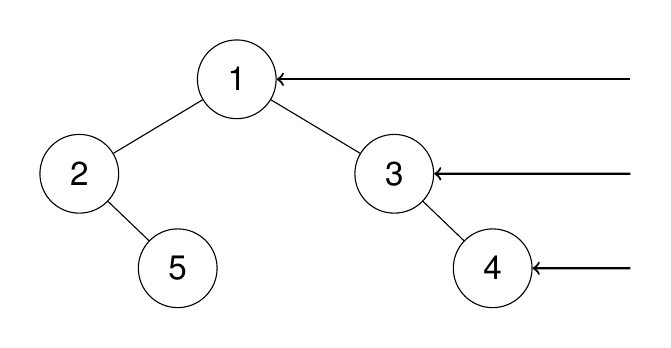
示例 2:
輸入:root = [1,2,3,4,null,null,null,5]
輸出:[1,3,4,5]
解釋:
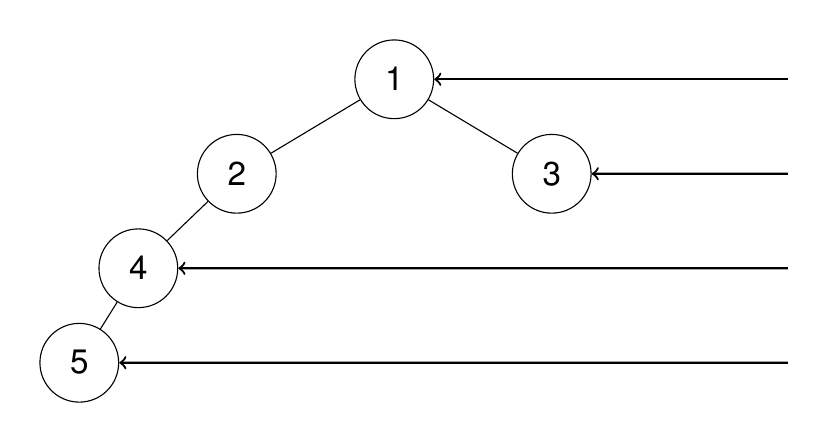
示例 3:
輸入:root = [1,null,3]
輸出:[1,3]
示例 4:
輸入:root = []
輸出:[]
提示:
- 二叉樹的節點個數的范圍是 [0,100]
- -100 <= Node.val <= 100
思考:層次遍歷+取層尾節點
核心是用隊列維護每一層節點,遍歷每層時直接提取最后一個節點的值加入結果——因層次遍歷按“左→右”順序收集下一層節點,層尾節點天然是該層最右側節點,無需額外判斷。
算法過程
- 邊界處理:若根節點
root為null(空樹),直接返回空結果數組。 - 初始化:創建結果數組
result(存儲右視圖節點值),隊列queue初始存入根節點(第一層僅根節點)。 - 層序循環(遍歷每一層):
- 記錄當前層節點數:用
size = queue.length獲取當前層總節點數(避免后續隊列添加子節點后長度變化); - 取層尾節點值:當前層最右側節點是隊列第
size-1個元素,將其val加入result; - 收集下一層節點:創建臨時數組
tmp,遍歷當前層所有節點,按“左子節點→右子節點”順序加入tmp(保證下一層節點仍按左→右排列,層尾為最右側節點); - 更新隊列:將隊列替換為
tmp(下一層節點),進入下一輪循環,直至隊列為空。
- 記錄當前層節點數:用
- 返回結果:返回
result,即二叉樹右視圖的節點值列表。
時空復雜度
- 時間復雜度:O(n),n為二叉樹節點總數。
原因:每個節點僅入隊、出隊各1次,取層尾節點值的操作也為O(n),總操作次數與節點數線性相關。 - 空間復雜度:O(m),m為二叉樹最寬層的節點數。
原因:隊列需存儲當前層所有節點,最壞情況(完全二叉樹最后一層)m=O(n/2)=O(n),最好情況(鏈狀樹,每層僅1個節點)m=1。
代碼
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[]}*/
var rightSideView = function(root) {const result = [];if (!root) return result; // 空樹返回空數組let queue = [root]; // 隊列:維護當前層節點while (queue.length) {const size = queue.length; // 固定當前層節點數(避免后續添加子節點影響)// 取當前層最后一個節點(最右側節點)的值,加入結果result.push(queue[size - 1].val);// 收集下一層節點(左→右順序,保證下一層層尾仍為最右側節點)let tmp = [];for (let node of queue) {if (node.left) tmp.push(node.left);if (node.right) tmp.push(node.right);}queue = tmp; // 切換到下一層}return result;
};
關鍵邏輯解析
-
為何按“左→右”收集下一層節點?
無論收集順序是左→右還是右→左,只要能準確找到“當前層最后一個節點”即可。按左→右收集是層次遍歷的常規習慣,且無需額外調整順序——隊列中當前層的最后一個元素,就是該層從右往左看的第一個可見節點。 -
為何要固定當前層節點數
size?
若不固定size,直接遍歷queue時,后續添加的下一層節點會混入當前層隊列,導致遍歷范圍錯誤。用size = queue.length提前鎖定當前層節點數,確保僅遍歷當前層節點,避免邏輯混亂。 -
對比深度優先(DFS)實現的優勢
層次遍歷(BFS)的優勢是“按層處理”,天然適合“取層尾節點”的需求,代碼邏輯直觀,無需維護深度參數;而DFS(如先右后左的前序遍歷)需記錄當前節點深度,僅在“首次訪問該深度”時記錄節點值,邏輯稍復雜。兩種方法時間復雜度均為O(n),空間復雜度相近,但層次遍歷更貼合右視圖的“層特性”。





)
算法)





)



)


