今天同樣是單調棧，第二題很重要。

第一題：

簡介：

本題可以說和上一題很是相似，只是有一點不同，數組是循環的。本題有兩種巧妙地解法，都不難。

第一種方法（也是第一個想出來的方法）：

拼接數組，我們將兩個相同的ｎｕｍｓ數組進行拼接這樣我們就可以保證第一個ｎｕｍｓ數組進行了循環的遍歷。此方法容易相處但是有很多弊端：例如浪費空間很多，也做了很多多余的操作，我們拼接數組后，還要剪切數組等等。

代碼實現：

vector<int> nextGreaterElements(vector<int>& nums) {stack<int> str;vector<int> path(nums.size()*2,0);vector<int> result(nums.size()*2,-1);str.push(0);int k=0;for(int i=0;i<nums.size()*2;i++){if(k==nums.size()) k=0;path[i] = nums[k];k++;}for(int i=1;i<path.size();i++){if(path[i]>path[str.top()]){while(!str.empty()&&path[i]>path[str.top()]){result[str.top()] = path[i];str.pop();}str.push(i);}else if(path[i] == path[str.top()]){str.push(i);}else{str.push(i);}}for(int i=0;i<nums.size();i++){result.pop_back();}return result;}

第二種方法（很巧妙的實現了循環遍歷數組）：

此種方法我們通過　［i％ｎｕｍｓ．ｓｉｚｅ（）］來實現我們重復遍歷數組的目的。

代碼實現：?

 vector<int> nextGreaterElements(vector<int>& nums) {vector<int> result(nums.size(), -1);if (nums.size() == 0) return result;stack<int> st;st.push(0);for (int i = 1; i < nums.size() * 2; i++) { // 模擬遍歷兩邊nums，注意一下都是用i % nums.size()來操作if (nums[i % nums.size()] < nums[st.top()]) st.push(i % nums.size());else if (nums[i % nums.size()] == nums[st.top()]) st.push(i % nums.size()); else {while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {result[st.top()] = nums[i % nums.size()];st.pop();}st.push(i % nums.size());}}return result;}

第二題：

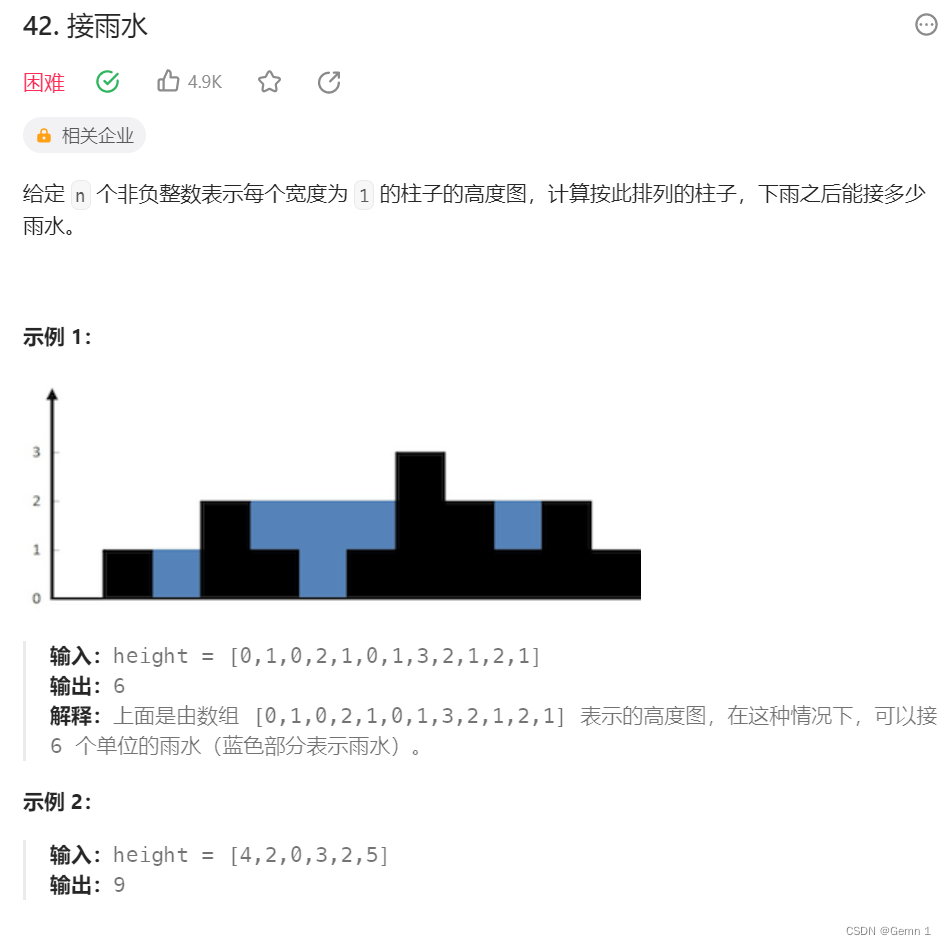
簡介：

本題是面試中考的概率很高的一題。

本題共有三種方法

暴力破解法

暴力法的重點在于如何求出單列的水的體積例如：

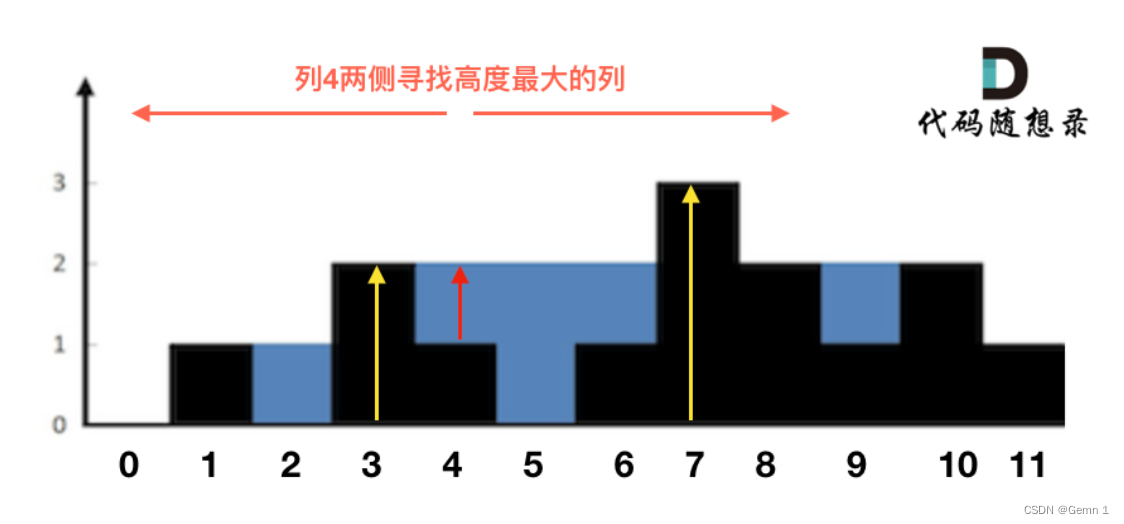
列4 左側最高的柱子是列3，高度為2（以下用lHeight表示）。

列4 右側最高的柱子是列7，高度為3（以下用rHeight表示）。

列4 柱子的高度為1（以下用height表示）

那么列4的雨水高度為 列3和列7的高度最小值減列4高度，即： min(lHeight, rHeight) - height。

列4的雨水高度求出來了，寬度為1，相乘就是列4的雨水體積了。

此時求出了列4的雨水體積。

我們遍歷每列然后將結果相加也就是最后的答案。

時間復雜度為O（ｎ）

代碼實現：

 int trap(vector<int>& height) {int sum = 0;for (int i = 0; i < height.size(); i++) {// 第一個柱子和最后一個柱子不接雨水if (i == 0 || i == height.size() - 1) continue;int rHeight = height[i]; // 記錄右邊柱子的最高高度int lHeight = height[i]; // 記錄左邊柱子的最高高度for (int r = i + 1; r < height.size(); r++) {if (height[r] > rHeight) rHeight = height[r];}for (int l = i - 1; l >= 0; l--) {if (height[l] > lHeight) lHeight = height[l];}int h = min(lHeight, rHeight) - height[i];if (h > 0) sum += h;}return sum;}

雙指針法

思路與暴力解法一樣，只是我們在代碼實現上有所不同，我們通過兩個數組將左邊柱子最大高度和右邊柱子最大高度都記錄下來。然后我們在遍歷時就省下了很多時間。時間復雜度O（n）

代碼實現：

  int trap(vector<int>& height) {if (height.size() <= 2) return 0;vector<int> maxLeft(height.size(), 0);vector<int> maxRight(height.size(), 0);int size = maxRight.size();// 記錄每個柱子左邊柱子最大高度maxLeft[0] = height[0];for (int i = 1; i < size; i++) {maxLeft[i] = max(height[i], maxLeft[i - 1]);}// 記錄每個柱子右邊柱子最大高度maxRight[size - 1] = height[size - 1];for (int i = size - 2; i >= 0; i--) {maxRight[i] = max(height[i], maxRight[i + 1]);}// 求和int sum = 0;for (int i = 0; i < size; i++) {int count = min(maxLeft[i], maxRight[i]) - height[i];if (count > 0) sum += count;}return sum;}

單調棧法

單調棧發與前兩個解法不同，前兩個解法是按列來計算，此解法為按行來計算。后面便利的過程建議去跟卡哥的視頻走一趟就明白了，或者自己模擬過程。

代碼實現：

  int trap(vector<int>& height) {if (height.size() <= 2) return 0; // 可以不加stack<int> st; // 存著下標，計算的時候用下標對應的柱子高度st.push(0);int sum = 0;for (int i = 1; i < height.size(); i++) {if (height[i] < height[st.top()]) {     // 情況一st.push(i);} if (height[i] == height[st.top()]) {  // 情況二st.pop(); // 其實這一句可以不加，效果是一樣的，但處理相同的情況的思路卻變了。st.push(i);} else {                                // 情況三while (!st.empty() && height[i] > height[st.top()]) { // 注意這里是whileint mid = st.top();st.pop();if (!st.empty()) {int h = min(height[st.top()], height[i]) - height[mid];int w = i - st.top() - 1; // 注意減一，只求中間寬度sum += h * w;}}st.push(i);}}return sum;}

總結：

?單調棧的題目從我的感覺來講就是明白運行過程，理清思路，進行遍歷，然后考慮好棧是遞增還是遞減，然后基本上大部分題的基礎思路就出來了。繼續加油！