P2568 GCD - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)https://www.luogu.com.cn/problem/P2568

大致題意：給定正整數n，求1<= x,y<=n 且 gcd（x，y）為素數的數對（x，y）有多少對。（n<=10^7)

思路：不如找n以內的所有的素數，然后統計每一個素數，是哪些數的最大公約數。

假設gcd（x，y）=p，設x=tp，y=rp；則 t與r必然互質。

由于x，y<=n，那么? t，r<=n/p。

所以，假設r更大，那么我們只要求1~r中與r互素的數字有多少個。

也就是求。然后將*2 ，

由于可以取遍1~n/p，

別忘了r=1，t=1，的時候也算了兩遍，所以

對于任意一個1~n的質數，其總方案就是：

最終的答案就是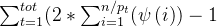

所以我們只需要用篩法求歐拉函數，同時求它的前綴和，

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>using namespace std;
const int N = 1e7 + 7;
int pri[N], phi[N], flag[N];  // 質數表， 歐拉函數 ， 標記函數
long long sumphi[N];  // 前綴和數組
int tot;// 有多少個質數
int main() {int n;cin >> n;phi[1] = sumphi[1] = 1;  //預處理 1 的情況for (int i = 2; i <= n; i++) {if (flag[i] == 0) {   //套線性篩的板子pri[tot++] = i;phi[i] = i - 1;   }sumphi[i] = sumphi[i - 1] + phi[i];    //處理前綴和for (int j = 0; j < tot and pri[j] * i <= n; j++) {  flag[i * pri[j]] = 1;if (i % pri[j] == 0) {phi[i * pri[j]] = pri[j] * phi[i];break;}else {phi[i * pri[j]] = (pri[j] - 1) * phi[i];}}}long long ans = 0;for (int i = 0; i < tot; i++) {ans += sumphi[n / pri[i]] * 2 - 1;}cout << ans;
}