目錄
1.什么是遞歸：
1.1遞歸的思想：
1.2遞歸的限制條件：
2.遞歸舉例：
2.1舉例1：求n的階乘：
2.1.1 分析和代碼實現：
?2.1.2圖示遞歸過程：
2.2舉例2：順序打印一個整數的每一位：
2.2.1分析和代碼實現：
2.2.2圖示遞歸過程：
1.什么是遞歸：
?遞歸是學習C語言函數繞不開的一個話題，那什么是遞歸呢
?遞歸其實是一種解決問題的方法，在C語言中，遞歸就是函數自己調用自己。
寫一個簡單的C語言遞歸代碼：
#include<stdio.h>
int main()
{printf("hehe\n");mian();return 0;
}上述就是一個簡單的遞歸程序，只不過上面的遞歸只是為了演示遞歸的基本形式，不是為了解決問題，代碼最終會陷入死遞歸，導致棧溢出（Stack overflow）。
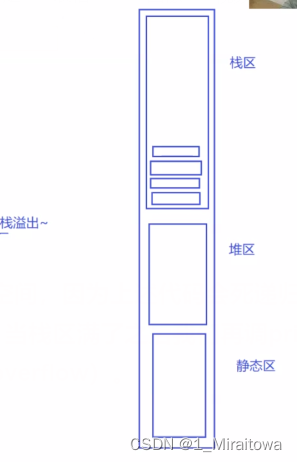
?棧溢出的原因：
?我們每次調用printf（）函數時都會在棧區開辟一塊空間，因為上述代碼會死遞歸，所以會一直調用printf（）函數，但是棧區的空間是有限的，當棧區滿了之后我們再調printf（）函數時，系統想繼續分配空間此時就會棧溢出（Stack overflow）。
1.1遞歸的思想：
把一個大型復雜的問題層層轉化為一個與原問題相似，但規模較小的子問題來求解；直到子問題不能再被拆分，遞歸就結束了。所以遞歸過程就是把大事化小的過程
遞歸中的遞就是遞推的意思，歸就是回歸的意思，接下來慢慢體會 。
1.2遞歸的限制條件：
遞歸在書寫的時候，有2個必要條件：
1.遞歸存在限制條件，當滿足這個限制條件時，遞歸便不再繼續。
2.每次遞歸調用之后越來越接近這個限制條件。（漸漸停下來）
在下面的例子中，我們會逐步體會這兩個限制條件
2.遞歸舉例：
2.1舉例1：求n的階乘：
階乘（factorial）：一個正整數的階乘是所有小于等于該數的正整數的積，且0的階乘為1，
自然數n的階乘寫作n！
2.1.1 分析和代碼實現：
以5！為例子我們進行分析
5！=5*4*3*2*1????????=????????5*4！
4！=?? 4*3*2*1????????=????????4*3！
3！=????? 3*2*1????????=????????3*2！
2！=????????? 2*1????????=????????2*1！
1！=???????????? 1????????=????????1*0！
0！=1
通過觀察5！我們可以發現當n>0時，n！=n*（n-1）！，當n=0時，n！=1。
如下圖所示：
?
?因此我們可以定義求n！函數為Fact（n），當n>0時，Fact（n）=n*Fact（n-1），當n=0時，Fact（n）=1。
代碼實現如下：
#include<stdio.h>
int Fact(int n)
{if (n > 0) {return n * Fact(n - 1);}else{return 1;}
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fact(n);printf("%d", ret);
}運行結果如下：
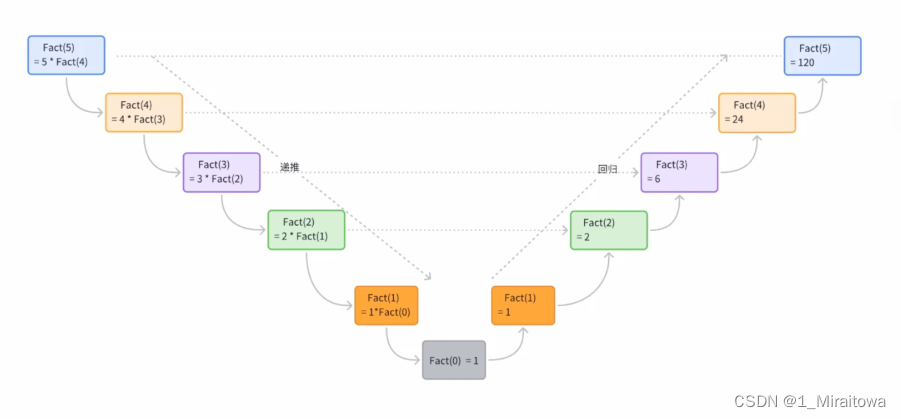
?2.1.2圖示遞歸過程：
2.2舉例2：順序打印一個整數的每一位：
輸入一個整數m，按照順序打印整數的每一位
例如：
輸入：1234??????????????? 輸出：1 2 3 4
輸入：520????????????????? 輸出：5 2 0
2.2.1分析和代碼實現：
這個題目，放在我們面前，首先想到的是，怎么得到這個數的每一位呢？
如果n是一位數，那么取出的數字就是它本身,如果n超過一位數（即n>9），就需要拆分每一位。
例如1234：
1234%10得到4，1234/10得到123，相當于去掉了4，繼續對123%10得到3，123/10得到12，以此類推，不斷重復%10和/? 10的操作，直到1234的每一位都得到；但是我們按照此方法得到的不是1 2 3 4而是倒著的4 3 2 1.
那么我們可以這么想，每一個數字的最低位置是最容易得到的，通過%10就可以得到
我們設想寫一個函數Print（）來打印n的每一位，如下表示：
Print（n）
如果n是1234，則表示為
Print（1234）//打印1234的每一位
其中1234中的4可以通過%10得到
那么Print（1234）可以分為兩步：
1.Print（1234/10）//相當于Print（123）打印123的每一位
2.printf（1234%10）//打印4
完成了上述兩個步驟就完成了1234的每一位打印
那么Print（123）又可以拆分為Print（123/10）+printf（123%10）
以此類推下去就有：
直到被打印的數字變成一位數的時候，就不再需要拆分，遞歸完成，有了上述的分析，代碼可以清晰的寫出，如下所示：
#include<stdio.h>
void Print(int n)
{if(n>9){Print(n / 10);printf("%d ", n % 10);}else{printf("%d ", n);}
}
int main()
{int n = 0;scanf_s("%d", &n);Print(n);
}運行結果如下：
2.2.2圖示遞歸過程：
以上便是我為大家帶來的函數遞歸的第一部分內容，若有不足，望各位大佬在評論區指出，謝謝大家！可以留下你們點贊、收藏和關注，這是對我極大的鼓勵，我也會更加努力創作更優質的作品。再次感謝大家！
)
