1. 集成學習
? ? ? ? 集成學習(ensemble learning)是現在非常火爆的機器學習方法。它本身不是一個單獨的機器學
習算法,而是通過構建并結合多個機器學習器來完成學習任務。也就是我們常說的“博采眾長”。集
成學習可以用于分類問題集成,回歸問題集成,特征選取集成,異常點檢測集成等等,可以說所有
的機器學習領域都可以看到集成學習的身影。

集成學習通過建立幾個模型來解決單?預測問題。它的?作原理是?成多個分類器/模型,各自獨
立地學習和作出預測。這些預測最后結合成組合預測,因此優于任何?個單分類的做出預測。?
?只要單分類器的表現不太差,集成學習的結果總是要好于單分類器的。

? ? ? ?對于訓練集數據,通過訓練若干個個體學習器,通過一定的結合策略,就可以最終形成一個強
學習器,以達到博采眾長的目的。集成學習有兩個主要的問題需要解決,第一是如何得到若干個個
體學習器,第二是如何選擇一種結合策略,將這些個體學習器集合成一個強學習器。

2. 集成學習例子?
對下面實例D1進行分類,得到兩個分類結果h1和h2:



對多個分類器的分類結果進行某種組合來決定最終的分類,以取得比單個分類器更好的性能:


定義:集成學習是使用一系列學習器進行學習,并使用某種規則把各個學習結果進行整合從而獲得
比單個學習器更好的學習效果的一種機器學習方法。如果把單個分類器比作一個決策者的話,集成
學習的方法就相當于多個決策者共同進行一項決策。
在概率近似正確(PAC)學習的框架中,一個概念(一個類),如果存在一個多項式的學習算法能
夠學習它,如果正確率很高,那么就稱這個概念是強可學習(strongly learnable)的。如果正確率
不高,僅僅比隨機猜測略好,那么就稱這個概念是弱可學習(weakly learnable)的。后來證明強
可學習與弱可學習是等價的。
3. 解決的問題
3.1 弱分類器之間的關系

第一種就是所有的個體學習器都是一個種類的,或者說是同質的。
第二種是所有的個體學習器不全是一個種類的,或者說是異質的。
個體學習器有兩種選擇:
第一種就是所有的個體學習器都是一個種類的,或者說是同質的。比如都是決策樹個體學習器,或
者都是神經網絡個體學習器。
第二種是所有的個體學習器不全是一個種類的,或者說是異質的。比如我們有一個分類問題,對訓
練集采用支持向量機個體學習器,邏輯回歸個體學習器和樸素貝葉斯個體學習器來學習,再通過某
種結合策略來確定最終的分類強學習器。
目前而言,同質個體學習器應用最廣泛,一般常說的集成學習的方法都是指的同質個體學習器。而
同質個體學習器使用最多的模型是CART決策樹和神經網絡。同質個體學習器按照個體學習器之間
是否存在依賴關系可以分為兩類,第一個是個體學習器之間存在強依賴關系,一系列個體學習器基
本都需要串行生成,代表算法是boosting系列算法,第二個是個體學習器之間不存在強依賴關系,
一系列個體學習器可以并行生成,代表算法是bagging和隨機森林(Random Forest)系列算法。
3.2 如何選擇個體學習器
考慮準確性和多樣性:
準確性指的是個體學習器不能太差,要有一定的準確度;
多樣性則是個體學習器之間的輸出要具有差異性。

3.3 弱分類器的組合策略
①平均法:對于數值類的回歸預測問題
思想:對于若干個弱學習器的輸出進行平均得到最終的預測輸出。
其中wi是個體學習器hi的權重,通常有wi≥0,![]()
②投票法:對于分類問題的預測
思想:多個基本分類器都進行分類預測,然后根據分類結果用某種投票的原則進行投票表決,按照
投票原則使用不同投票法:一票否決? 、閾值表決 、 少數服從多數。
閾值表決:首先統計出把實例x劃分為Ci和不劃分為Ci的分類器數目分別是多少,然后當這兩者比
例超過某個閾值的時候把x劃分到Ci。
③學習法:之前的方法都是對弱學習器的結果做平均或者投票,相對比較簡單,但是可能學習誤差
較大。代表方法是Stacking。
思想:不是對弱學習器的結果做簡單的邏輯處理,而是再加上一層學習器,分為2層。第一層是用
不同的算法形成T個弱分類器,同時產生一個與原數據集大小相同的新數據集,利用這個新數據集
和一個新算法構成第二層的分類器。

4. 集成學習方法
根據個體學習器的生成方式,目前的集成學習方法大致可分為兩類:
Boosting:個體學習器間存在強依賴關系,必須串行生成的序列化方法;串行:下一個分類器只
在前一個分類器預測不夠準的實例上進行訓練或檢驗。
Bagging:個體學習器間不存在強依賴關系,可同時生成的并行化方法。并行:所有的弱分類器都
給出各自的預測結果,通過組合把這些預測結果轉化為最終結果。
4.1?Boosting
重賦權法:即在訓練過程的每一輪中,根據樣本分布為每一個訓練樣本重新賦予一個權重。對無法
接受帶權樣本的基學習算法,則可以通過重采樣法來處理,即在每一輪的學習中,根據樣本分布對
訓練集重新進行采樣,在用重采樣而來的樣本集對基學習器進行訓練。
代表算法:
Adboost,決策樹+adboost=提升樹
GBDT(Gradient BoostDecision Tree)梯度提升決策樹,決策樹+Gradient Boosting=GBDT
其他叫法: Gradient Tree Boosting,GBRT (Gradient BoostRegression Tree) 梯度提升回歸樹
??????????????????? MART (MultipleAdditive Regression Tree) 多決策回歸樹,Tree Net決策樹網絡

4.2?Bagging (bootstrap aggregation )
從樣本集中用Bootstrap采樣選出n個樣本,在所有屬性上,對這n個樣本建立分類器(CART or
SVM or ...),重復以上兩步m次,i.e.build m個分類器(CART or SVM or ...)。將數據放在這m
個分類器上跑,最后vote看到底分到哪一類。
Bootstrap方法是非常有用的一種統計學上的估計方法。 Bootstrap是對觀測信息進行再抽樣,進而
對總體的分布特性進行統計推斷。Bootstrap是一種有放回的重復抽樣方法,抽樣策略就是簡單的
隨機抽樣。
![]()
隨機森林:決策樹+bagging=隨機森林

4.3 兩者的區別
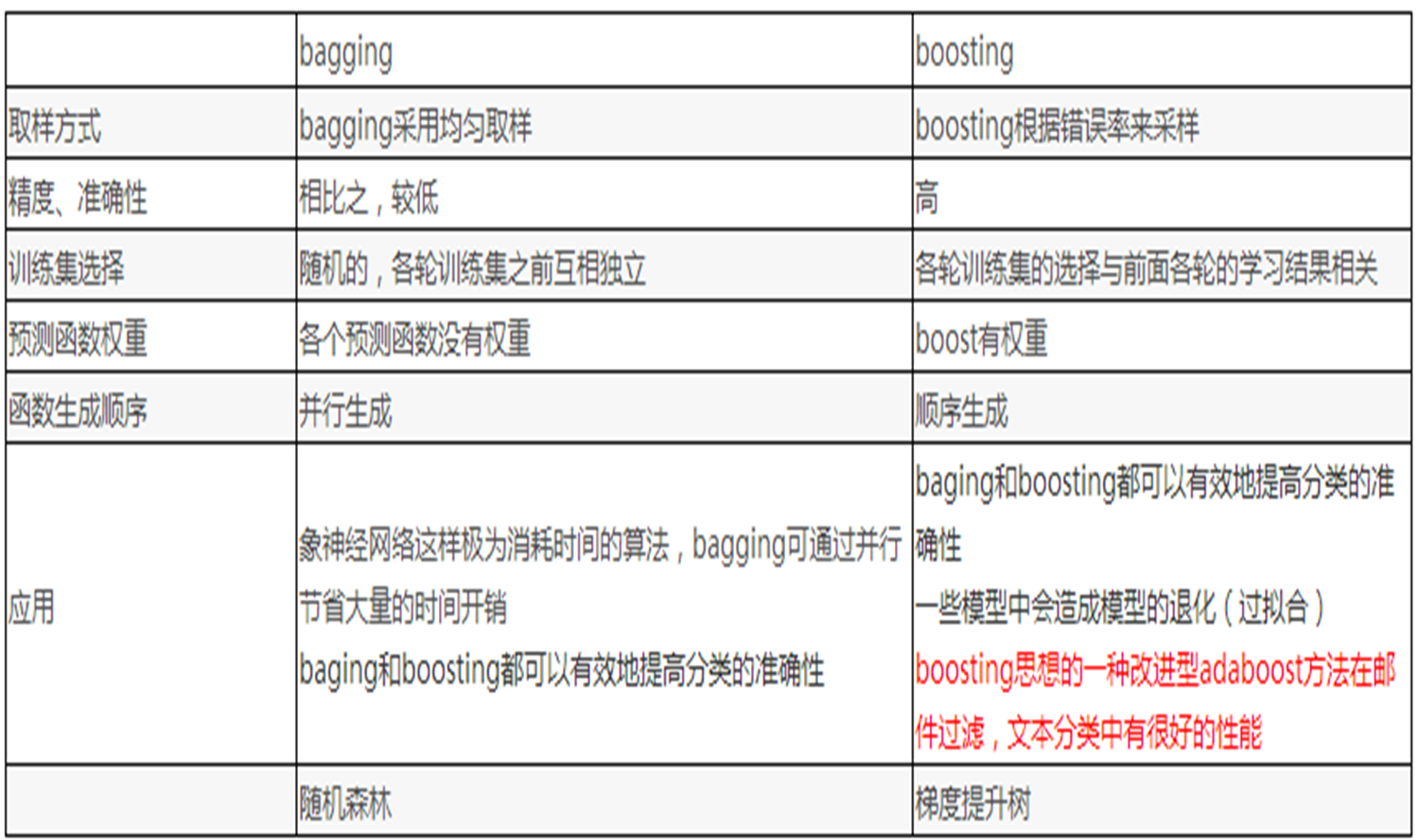
從偏差-方差分解的角度:
偏差(bias) :描述的是預測值的期望與真實值之間的差距。偏差越大,越偏離真實數據。
方差(variance) :描述的是預測值的變化范圍,離散程度,也就是離其期望值的距離。
方差越大,數據的分布越分散。
Boosting主要關注降低偏差:偏差刻畫了學習算法本身的擬合能力,Boosting思想,對判斷錯誤的
樣本不停的加大權重,為了更好地擬合當前數據,所以降低了偏差,因此Boosting能基于泛化性能
相當弱的學習器構建出很強的集成。Boosting是把許多弱的分類器組合成一個強的分類器。
Bagging主要是降低方差:度量了同樣大小的數據集的變動所導致的學習性能的變化。刻畫了數據
擾動所造成的影響。 Bagging思想,隨機選擇部分樣本來訓練處理不同的模型,再綜合來減小方
差,因此它在不剪枝決策樹、神經網絡等易受樣本擾動的學習器上效果更明顯。Bagging是對許多
強(甚至過強)的分類器求平均。?




真題解析)




-Part.17 安裝Spark2)
)





Tiki-taka算法(TTA)求解無人機三維路徑規劃研究(MATLAB))


