原文地址
源代碼

Abstract

我們提出了一個簡單的、高度模塊化的圖像分類網絡體系結構。我們的網絡是通過重復構建塊來構建的，該構建塊聚合了具有相同拓撲結構的一組變換。我們的簡單設計產生了一個同質的、多分支的體系結構，只有幾個超參數需要設置。這個策略暴露了一個新的維度，我們稱之為“基數”(轉換集合的大小)，作為深度和寬度維度之外的一個重要因素。在ImageNet-1K數據集上，我們的經驗表明，即使在維持復雜性的限制條件下，增加基數也能夠提高分類精度。此外**，當我們增加容量時，增加基數比加深或擴大寬度更有效**。我們的模型ResNeXt是我們進入ILSVRC 2016分類任務的基礎，我們在該任務中獲得了第二名。我們在ImageNet-5K集和COCO檢測集上進一步研究了ResNeXt，也顯示出比ResNet更好的結果

1. Introduction

視覺識別研究正經歷著從“特征工程”到“網絡工程”的過渡[25,24,44,34,36,38,14]。與傳統的手工設計特征(例如SIFT[29]和HOG[5])相比，神經網絡從大規模數據中學習的特征[33]在訓練過程中需要最少的人工參與，并且可以轉移到各種識別任務中[7,10,28]。然而，人類的努力已經轉移到設計更好的網絡架構來學習表征
簡要介紹了下以前的backbone，并diss了下他們的不足

former work

VGG-nets展示了一種簡單而有效的構建深度網絡的策略：把相同形狀的塊堆疊起來
該策略被ResNets[14]繼承，ResNets堆疊相同拓撲的模塊。這個簡單的規則減少了超參數的自由選擇，并且深度暴露為神經網絡的一個基本維度。此外，我們認為該規則的簡單性可以降低對特定數據集過度適應超參數的風險。VGG-nets和ResNets的魯棒性已被各種視覺識別任務[7,10,9,28,31,14]以及涉及語音[42,30]和語言[4,41,20]的非視覺任務證明
與VGG-nets不同，Inception模型家族[38,17,39,37]已經證明，精心設計的拓撲結構能夠以較低的理論復雜性實現令人信服的準確性
Inception模型隨著時間的推移而發展[38,39]，但是一個重要的共同屬性是分裂-轉換-合并策略。在Inception模塊中，輸入被分成幾個低維嵌入(通過1×1卷積)，由一組專門的過濾器(3×3, 5×5等)進行轉換，并通過連接進行合并。可以證明，該體系結構的解空間是運行在高維嵌入上的單個大層(例如5×5)的解空間的嚴格子空間。Inception模塊的拆分-轉換-合并行為被期望接近大型和密集層的表示能力，但是在相當低的計算復雜性下

our work

在本文中，我們提出了一個簡單的架構，它采用了VGG/ResNets的重復層策略，同時以一種簡單、可擴展的方式利用了分裂-轉換-合并策略。我們的網絡中的一個模塊執行一組轉換，每個轉換都在一個低維嵌入上，其輸出通過求和來聚合。我們追求這個想法的一個簡單實現——要聚合的轉換都是相同的拓撲(例如，圖1(右))。這種設計允許我們擴展到任何大量的轉換，而無需專門的設計
有趣的是，在這種簡化的情況下，我們發現我們的模型還有另外兩種等效形式(圖3)。圖3(b)中的重新表述看起來類似于Inception- ResNet模塊[37]，因為它連接了多條路徑;但是我們的模塊與所有現有的Inception模塊的不同之處在于，我們所有的路徑都共享相同的拓撲結構，因此路徑的數量可以很容易地作為一個要研究的因素被隔離出來。在更簡潔的重新表述中，我們的模塊可以通過Krizhevsky等人的分組卷積(groups convolutions)24進行重塑，然而，這已經被開發為一種工程折衷方案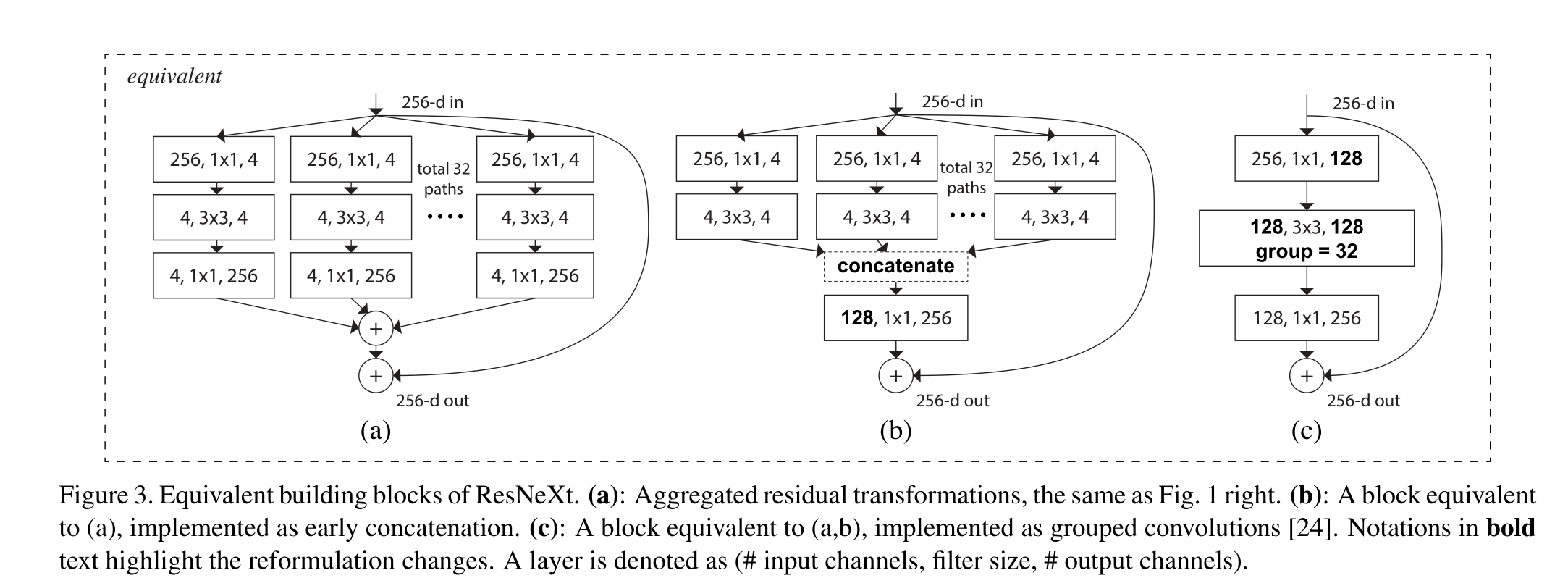

(a):聚合殘差變換，與圖1右圖相同。(b):相當于(A)的塊，作為早期連接實現。?:相當于(A,b)的塊，實現為分組卷積[24]。加粗文字的注釋突出了重新表述的變化。層表示為(#輸入通道，過濾器大小，#輸出通道)

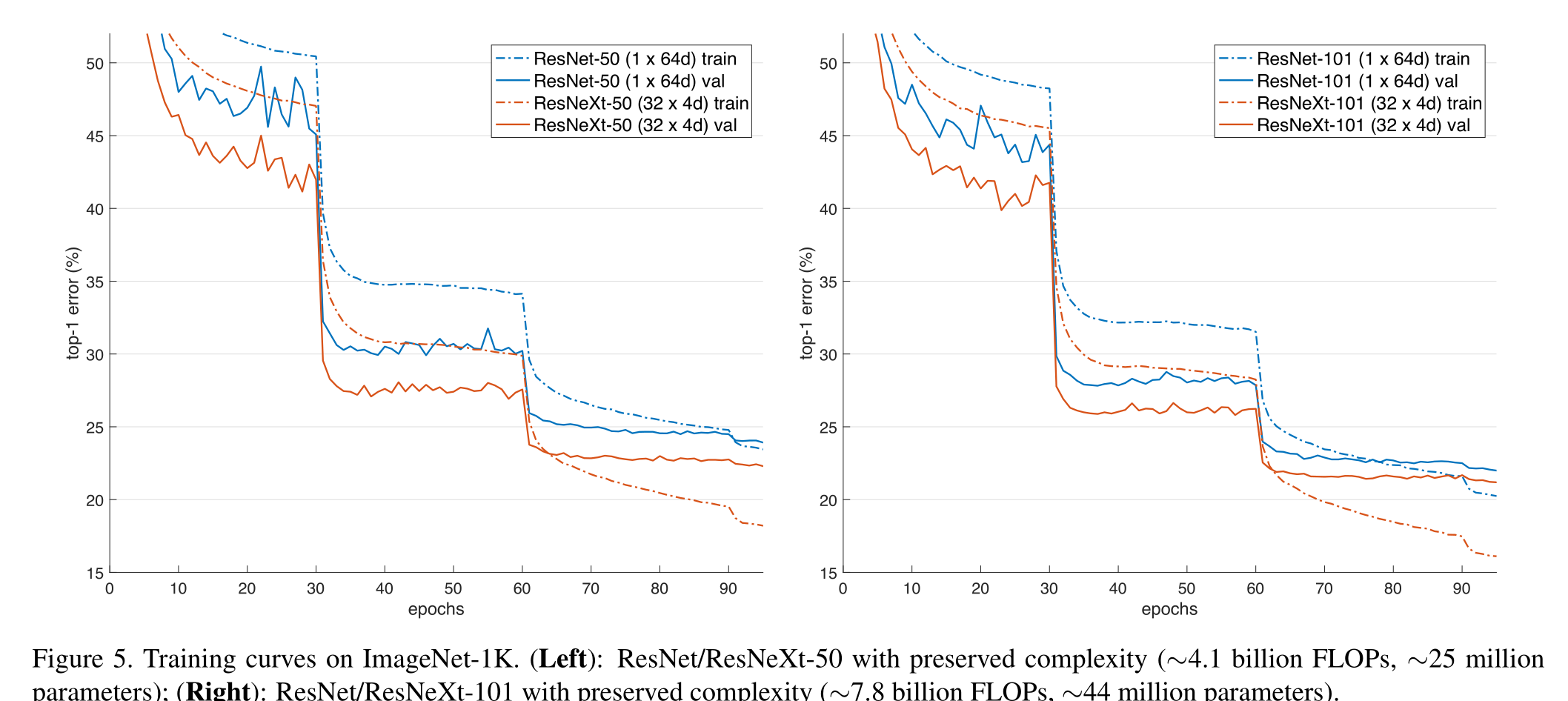
我們通過經驗證明，即使在保持計算復雜性和模型大小的限制條件下，我們的聚合變換也優于原始ResNet模塊——例如，圖1(右)的設計是為了保持圖1(左)的FLOPs復雜性和參數數量。我們強調，雖然通過增加容量(更深入或更廣泛)來提高準確性相對容易，但在保持(或降低)復雜性的同時提高準確性的方法在文獻中很少

我們的方法表明，除了寬度和深度的維度外，基數(變換集的大小)是一個具體的、可測量的維度，這是至關重要的。實驗表明，增加基數是一種比深度或寬度更有效的獲得精度的方法，特別是當深度和寬度開始使現有模型的收益遞減時

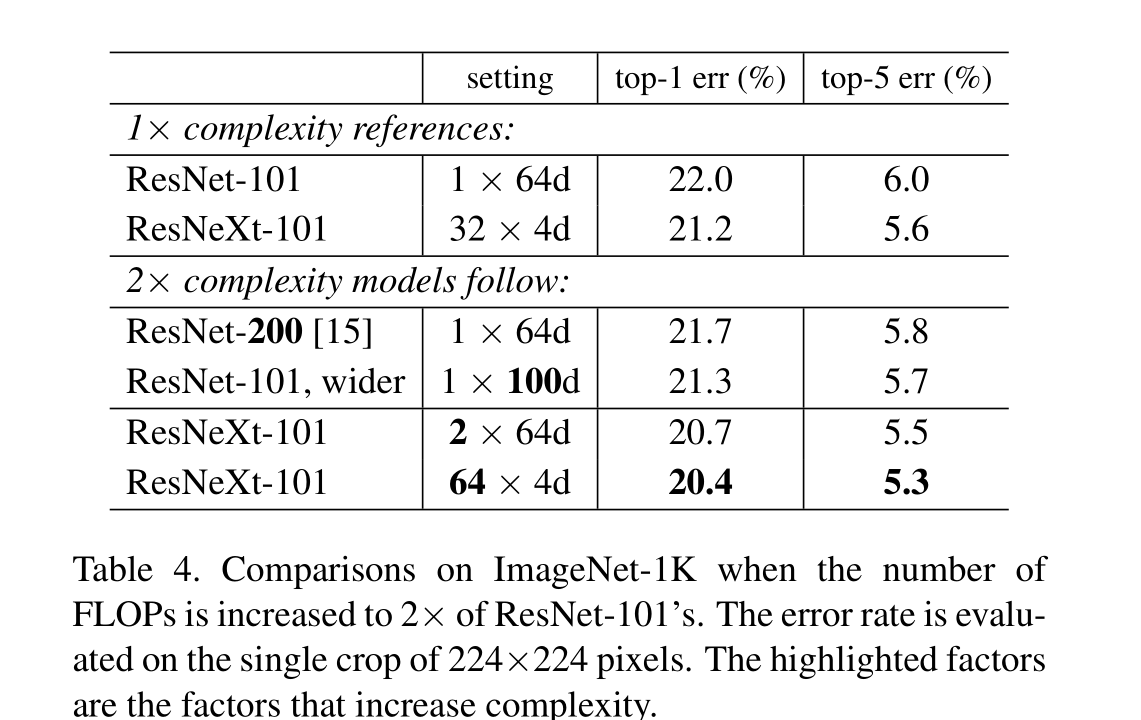
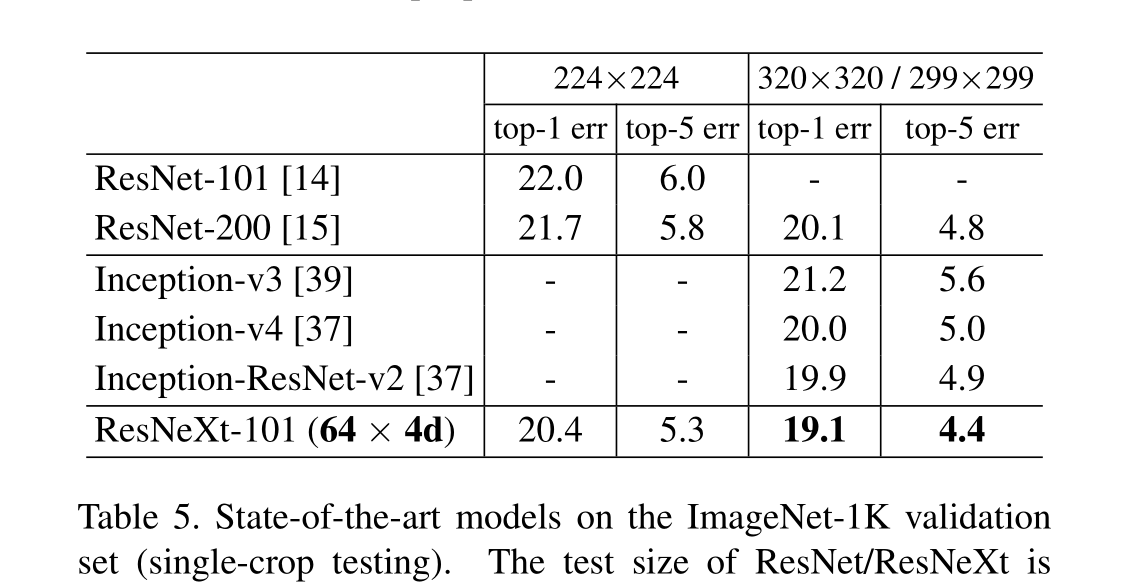
我們的神經網絡，命名為ResNeXt(建議下一個維度)，在ImageNet分類數據集上優于ResNet-101/152 [14]， ResNet- 200 [15]， Inception-v3[39]和Inception-ResNet-v2[37]。特別是，101層的ResNeXt能夠達到比ResNet-200更好的精度[15]，但只有50%的復雜性。此外，ResNeXt展示了比所有Inception模型更簡單的設計。ResNeXt是我們參加ILSVRC 2016分類任務的基礎，我們獲得了第二名。本文在更大的ImageNet-5K集和COCO對象檢測數據集上進一步評估了ResNeXt[27]，顯示出比ResNet同類產品更好的準確性。我們希望ResNeXt也能很好地推廣到其他視覺(和非視覺)識別任務

2. Related Work

多分支卷積網絡

Inception模型[38,17,39,37]是成功的多分支架構，其中每個分支都是精心定制的。ResNets[14]可以被認為是一個雙分支網絡，其中一個分支是身份映射。深度神經決策森林[22]是具有學習分裂函數的樹形多分支網絡

分組卷積

分組卷積的使用可以追溯到AlexNet論文[24]，如果不是更早的話。Krizhevsky等人[24]給出的動機是將模型分布在兩個gpu上。分組卷積由Caffe [19]， Torch[3]等庫支持，主要是為了AlexNet的兼容性。據我們所知，很少有證據表明利用分組卷積來提高準確率。**分組卷積的一種特殊情況是通道型卷積，其中組的數量等于通道的數量。**通道型卷積是[35]中可分離卷積的一部分

壓縮卷積網絡

分解(在空間[6,18]和/或通道[6,21,16]級別)是一種廣泛采用的技術，用于減少深度卷積網絡的冗余并加速/壓縮它們。Ioannou等人[16]提出了一種“根”模式的網絡進行約簡計算，根中的分支通過分組卷積實現。這些方法[6,18,21,16]在較低的復雜性和較小的模型尺寸下顯示了精度的優雅妥協。而不是壓縮，我們的方法是一個架構，經驗顯示出更強的表征能力

Ensembling

對一組獨立訓練的網絡進行平均是提高準確率的有效解決方案[24]，在識別競賽中被廣泛采用[33]。Veit等人[40]將單個ResNet解釋為較淺網絡的集合，這是由ResNet的加性行為造成的[15]。我們的方法利用加法來聚合一組轉換。但我們認為，將我們的方法視為集成是不精確的，因為要聚合的成員是聯合訓練的，而不是獨立訓練的。

3. Method

3.1. Template

我們采用高度模塊化的VGG/ResNets設計，我們的網絡由一堆殘差塊組成
這些塊具有相同的拓撲結構，并且受VGG/ResNets Inception的兩個簡單規則的約束:(i)如果產生相同大小的空間映射，則塊共享相同的超參數(寬度和過濾器大小)，并且(ii)每次當空間映射被下采樣2倍時，塊的寬度（通道數）乘以2倍。第二條規則確保所有塊的計算復雜度(以flop(浮點運算，以乘法加的次數計算)為單位)大致相同
有了這兩條規則，我們只需要設計一個模板模塊，一個網絡中的所有模塊都可以據此確定。所以這兩條規則大大縮小了設計空間，使我們能夠專注于幾個關鍵因素。這些規則構建的網絡如表1所示，C指的是基數 。4d指的是通道數為4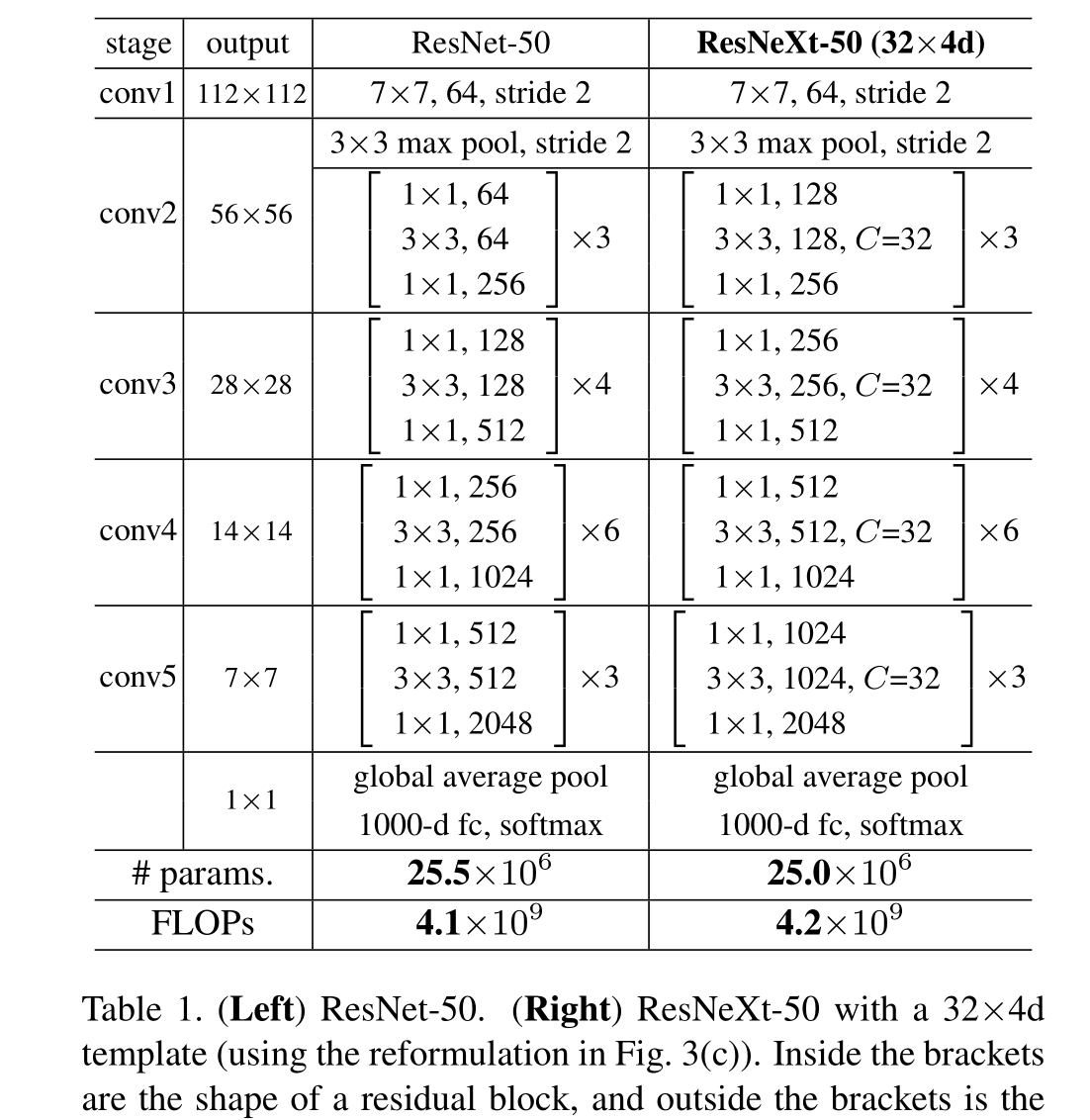

3.2. Revisiting Simple Neurons

人工神經網絡中最簡單的神經元執行內積(加權和)，這是由全連接層和卷積層完成的初等變換。內積可以看作是集合變換的一種形式:

式中x = [x 1,x 2，…]，x D是神經元的D通道輸入向量，w i是第i個通道的濾波器權值。這種操作(通常包括一些非線性輸出)被稱為“神經元”。見圖2

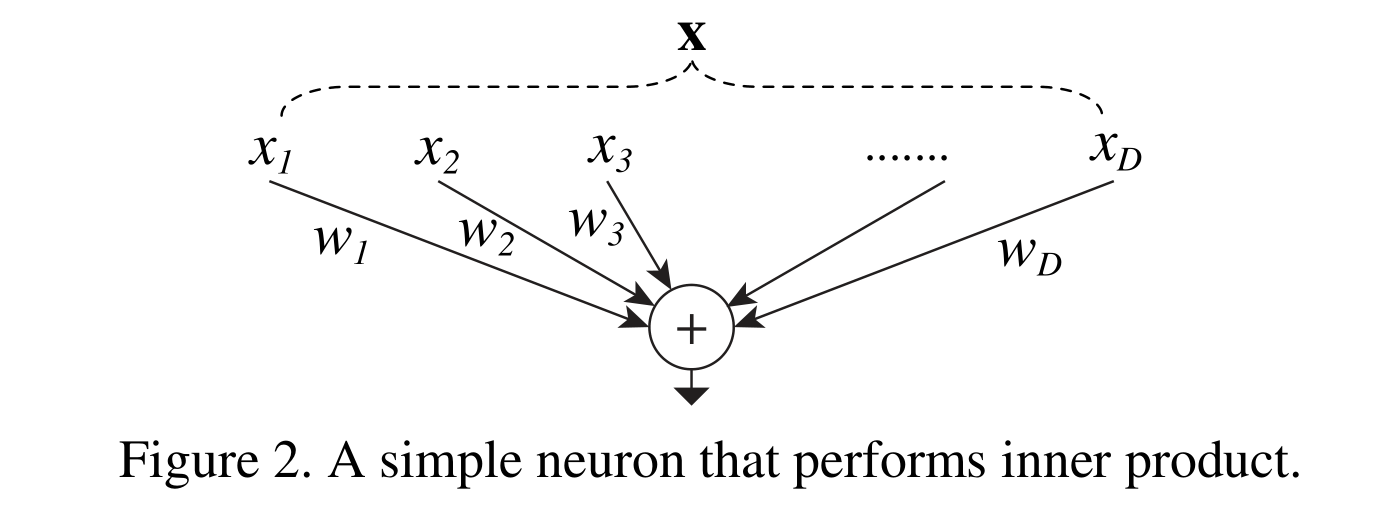
上述操作可以重新轉換為拆分、轉換和聚合的組合。
(i)分割:將向量x分割為一個低維嵌入，在上面，它是一個一維子空間xi
(ii)變換:對低維表示進行變換，在上面，它被簡單地縮放為:wi x i
(iii)聚合:所有嵌入中的轉換通過ΣD i=1

3.3. Aggregated Transformations

給定上述對一個簡單神經元的分析，我們考慮用一個更一般的函數代替初等變換(wi x i)，它本身也可以是一個網絡。與“Network-in-Network”[26]相反，我們表明我們的“Network-in-Neuron”沿著一個新的維度擴展。
形式上，我們將聚合轉換表示為:

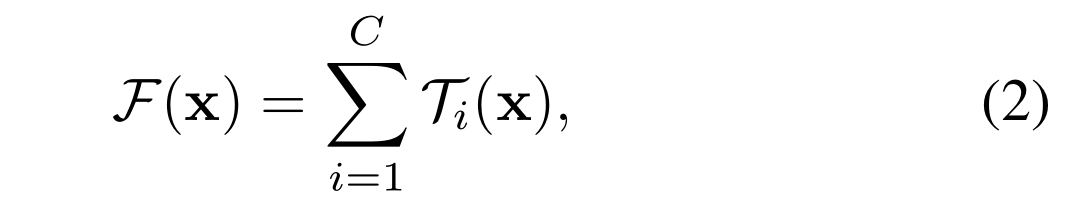
其中Ti (x)可以是任意函數。類似于一個簡單的神經元，T i應該將x投射到一個(可選的低維)嵌入中，然后對其進行變換
在公式(2)中，C是要聚合的轉換集合的大小。我們將C稱為基數[2]。在Eqn.(2)中，C的位置與Eqn.(1)中D的位置相似，但C不必等于D，可以是任意數。雖然寬度的維度與簡單變換(內積)的數量有關，但我們認為基數的維度控制著更復雜變換的數量。我們通過實驗證明，基數是一個重要的維度，可以比寬度和深度的維度更有效

在本文中，我們考慮了一種設計變換函數的簡單方法:所有的T具有相同的拓撲。這擴展了vgg風格的重復相同形狀的層的策略，這有助于隔離一些因素并擴展到任何大量的轉換。我們將單個轉換t1設置為瓶頸形架構[14]，如圖1(右)所示。在這種情況下，每個t1中的第一個1×1層產生低維嵌入。

Eqn.(2)中的聚合變換作為殘差函數14: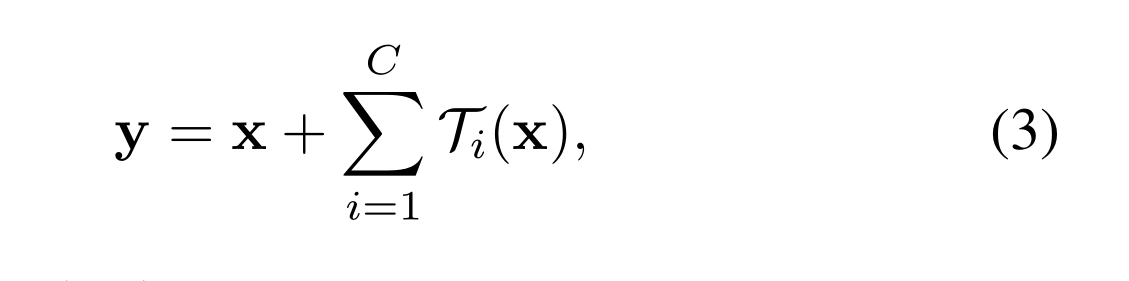
與Inception-ResNet的關系：一些張量操作表明，圖1(右)中的模塊(也顯示在圖3(a)中)等價于圖3(b)。圖3(b)與Inception-ResNet[37]塊相似，在殘差函數中涉及分支和連接。但與所有Inception或Inception- resnet模塊不同，我們在多個路徑中共享相同的拓撲結構。我們的模塊只需要最少的額外工作來設計每條路徑
與分組卷積的關系：使用分組卷積的表示法，上述模塊變得更加簡潔[24]。圖3?說明了這種重新配方。所有的低維嵌入(第一個1×1層)都可以被單個更寬的層(例如，圖3?中的1×1, 128-d)所取代。分裂本質上是由分組卷積層在將其輸入通道分成組時完成的。圖3?中的分組卷積層每形成32組卷積，其輸入輸出通道為4維。分組卷積層將它們連接起來作為層的輸出。圖3?中的塊看起來與圖1(左)中的原始瓶頸剩余塊相似，只是圖3?是一個更寬但稀疏連接的模塊

我們注意到，只有當塊的深度≥3時，重新表述才會產生非平凡拓撲。如果該塊的深度為2(例如，[14]中的基本塊)，則重新表述通常會導致一個寬而密集的模塊。如圖4所示
討論：我們注意到，盡管我們提出了顯示串聯(圖3(b))或分組卷積(圖3?)的重新表述，但這種重新表述并不總是適用于Eqn(3)的一般形式，例如，如果變換ti采用任意形式并且是異質的。我們在本文中選擇使用同質表單，因為它們更簡單和可擴展。在這種簡化情況下，圖3?形式的分組卷積有助于簡化實現

3.4. Model Capacity

我們的模型在保持模型復雜性和參數數量的情況下提高了準確性。這不僅在實踐中很有趣，更重要的是，參數的復雜性和數量代表了模型的固有能力，因此經常作為深度網絡的基本屬性進行研究[8]

瓶頸寬度通常指的是ResNeXt中的瓶頸結構中最中間那一層的通道數或特征圖的維度。ResNeXt的基本結構由一系列的瓶頸塊組成，其中的瓶頸塊包含了三個卷積層，中間那一層通常是瓶頸寬度所指的地方。這個瓶頸寬度的選擇可以影響模型的復雜度和性能

當我們評估不同的基數C時，同時保持復雜性，我們希望最小化對其他超參數的修改。我們選擇調整瓶頸的寬度(例如圖1(右)中的4-d)，因為它可以與塊的輸入和輸出隔離。這種策略不會改變其他超參數(深度或塊的輸入/輸出寬度)，因此有助于我們關注基數的影響
在圖1(左)中，原始ResNet瓶頸塊[14]具有256·64+3·3·64·64+64·256≈70k參數和比例FLOPs(在相同的特征圖大小下)。當瓶頸寬度為d時，我們在圖1(右)中的模板具有: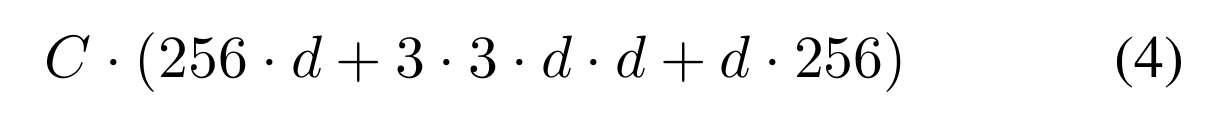
參數和比例FLOPs。當C = 32, d = 4時，Eqn.(4)≈70k。表2顯示了基數C和瓶頸寬度d之間的關系

基數和寬度之間的關系(對于conv2的模板)，在殘差塊上大致保留復雜度。對于conv2的模板，參數的數量為~ 70k。FLOPs的數量為~ 2.2億(conv2的# params×56×56)

因為我們在3.1節中采用了這兩個規則，所以上面的近似相等在ResNet瓶頸塊和ResNeXt之間的所有階段都是有效的(除了特征映射大小變化的子采樣層)。表1比較了原始的ResNet-50和具有類似容量的ResNeXt-50。我們注意到，復雜性只能近似地保留，但復雜性的差異很小，不會影響我們的結果

4. Experiment