該內容為重拾部分線性代數知識的學習筆記,內容上更多的是為了解決問題而學習的內容,并非系統化的學習。
針對的問題為:Music算法推導求解過程中的矩陣計算知識。
學習的內容包括:矩陣原理、矩陣行列式、矩陣的秩、線性變換矩陣變換、單位矩陣與逆矩陣、特征值和特征向量。
推薦學習視頻:bilibili的視頻:【線性代數全集從入門到精通(清楚易懂,看過的都說好,哈哈)】 https://www.bilibili.com/video/BV1wL411H7x1/?share_source=copy_web&vd_source=a0df23ab5f45bf4a580c20684f4a6705
一. 矩陣
-
線性方程組
線性方程組,多元x1 x2 x3等組成的線性方程組。線性方程組的解只有三種情況:0個解、1個(組)解和無窮多個解。
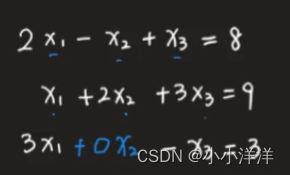
-
增廣矩陣
增廣矩陣為系數矩陣+常數項矩陣,是一種更簡單的表達。

-
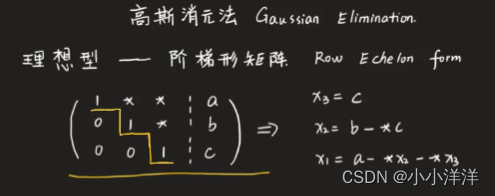
理想矩陣:階梯型矩陣、對角矩陣
通過對矩陣進行初等行變換,即行的倍數、行的疊加、行的倍數再疊加,矩陣的解不變。
從最下面一行開始消元,得到理想型矩陣可以方便求解元,該方法叫做高斯消元法。
階梯型矩陣就可以方便求解,對角矩陣則是更加理想的矩陣。
-
矩陣與向量
空間中的向量,可以用多個正交單位向量的組合表示。
多個向量的線性組合為這些向量的向量空間。
線性相關:多個向量的線性組合能夠等于0,其中他們的系數不全為0,即線性相關,否則線性無關。
定義:n+1個n維向量一定是線性相關的。因為n個不相關的向量已經組成了整個n維的自由空間,多一個肯定是在這個自由空間中的。
向量的計算:數乘、加法、線性組合。

-
齊次方程組
齊次方程組的常數矩陣為0,即Ax = 0

-
矩陣乘法
矩陣乘法中,左邊矩陣的列數要等于右邊矩陣的行數。
二、矩陣行列式
- 行列式可以Det(A)表示
- 行列式為符號系數+子矩陣行列式的疊加。
三、矩陣秩
- 秩的定義
矩陣的秩為最高階非零子式的階數。

- 秩對求解個數的意義
系數矩陣的秩=增廣矩陣的秩:1個解
系數矩陣的秩<增廣矩陣的秩:0個解
系數矩陣的秩>增廣矩陣的秩:無窮個解
四、線性變換、矩陣變換
- 線性變換和矩陣變換
這兩種變換是可以在一定程度上轉換的。
五、單位矩陣與逆矩陣
- 單位矩陣

- 逆矩陣
逆矩陣與原矩陣的乘積為單位矩陣。
逆矩陣的計算可以由下述公式計算,分母為矩陣行列式,也可以用Det(A)表示,選取最佳的一行(0比較多的行)進行計算。分子為伴隨矩陣。


六、特征值與特征向量
-
特征值和特征向量
矩陣和特征向量的乘積,正好為一個特征值與該特征向量的乘積。即矩陣的乘積,只改變該方向的大小,而不改變方向。
特征向量表達了方向,特征值表達了大小。
個人理解:特征向量意味著該矩陣在這個方向上的映射。

-
特征值計算
Ax = λx
Ax = λIx
(A-λI)x = 0
Det(A-λI) = 0
得到多個特征值 -
特征向量的計算
帶入特征值到上式,進行計算和求解。

-
意義
幾何意義為變換效果只發生縮放,不發生其他如旋轉、平移。
代數意義為矩陣的內部結構進行了分解和化解。
七、協方差矩陣
- 協方差矩陣
個人理解:表達了兩個矩陣之間的關聯性。


)




)
)


存儲技術專家成長路線)







