四元數，旋轉矩陣，旋轉向量，歐拉角

一、歐拉角

1、歐拉角是表達旋轉的最簡單的一種方式，形式上它是一個三維向量，其值分別代表物體繞坐標系三個軸(x,y,z軸）的旋轉角度，默認旋轉正向為逆坐標軸逆時針方向。

2、在旋轉過程中，xyz軸方向并不是固定不變的，而是隨著前面的旋轉而改變。比如如果繞 x 軸旋轉 90 度，那么旋轉后的 y 軸正向將指向原始的 z 軸方向，而旋轉后的 z 軸正向將指向 y 軸負向。由此可以看出，歐拉角對應的具體旋轉與 xyz 軸的旋轉順序是有關的，相同的 xyz 旋轉角度，如果按 xyz 的順序進行旋轉使用按 zyx 的順序進行旋轉，得到的結果是不一致的。

3、在具體應用中，xyz 軸朝向不固定，需要具體情況具體分析。

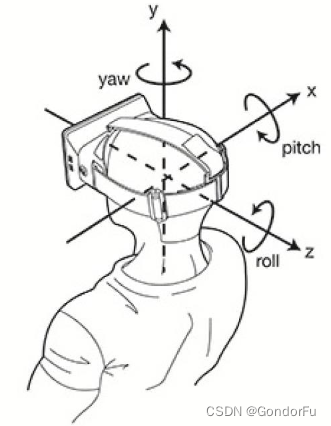
1. pitch：繞 x 軸旋轉，
2. yaw：繞 y 軸旋轉，
3. roll：繞 z 軸旋轉，

4、歐拉角表示最大的問題是存在萬向鎖問題。萬向鎖（Gimbal lock）是在使用動態歐拉角表示三維物體的旋轉時出現的問題。一旦選擇±90°作為pitch角，就會導致第一次旋轉和第三次旋轉等價，整個旋轉表示系統被限制在只能繞豎直軸旋轉，丟失了一個表示維度。

二、四元數

四元數通過四個實數描述三維旋轉，，其中?。

三、旋轉向量

旋轉向量用一個三維向量來表示三維旋轉變換，該向量的方向是旋轉軸，其模則是旋轉角度。

轉換方法

一、scipy.spatial.transform.Rotation

官方文檔：

https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.transform.Rotation.html#scipy.spatial.transform.Rotation

from scipy.spatial.transform import Rotation as R# 從四元數加載
r = R.from_quat([0, 0, np.sin(np.pi/4), np.cos(np.pi/4)])# 從旋轉矩陣加載
r = R.from_matrix([[0, -1, 0],[1, 0, 0],[0, 0, 1]])# 從旋轉向量加載
r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))# 從歐拉角加載
r = R.from_euler('zyx', [
[90, 0, 0],
[0, 45, 0],
[45, 60, 30]], degrees=True)# 使用四元數表示
r.as_quat()# 使用旋轉矩陣表示
r.as_matrix()# 使用旋轉向量表示
r.as_rotvec()# 使用歐拉角表示
r.as_euler('zyx', degrees=True)# 取逆
inv_r = r.inv()# 對點進行旋轉
r.apply(v)

二、pyquaternion.Quaternion

官方文檔：https://kieranwynn.github.io/pyquaternion/

r = Quaternion([w, x, y, z]).rotation_matrix

旋轉矩陣和平移向量的特殊操作

如果給定 A2B 的旋轉矩陣和平移向量，但是需要 B2A 的旋轉矩陣和平移向量，可以如此操作：

R_B2A = np.linalg.inv(R_A2B)
T_B2A = -np.dot(R_A2B, T_A2B)