數據結構——堆的實現

堆的實現-----C語言版

  • 目錄：
  • 一、堆的實現
    • 1.1堆的定義
    • 1.2堆的實現
      • 1.2.1堆的各個接口
      • 1.2.2堆的向上調整
      • 1.2.3堆的向下調整
      • 1.2.4堆的定義聲明和初始化
      • 1.2.5堆的數據處理
      • 1.2.6堆的判空和堆的數據個數以及堆銷毀
      • 1.2.7堆的代碼實現
  • 二、TOP—K問題

目錄：

一、堆的實現

1.1堆的定義

堆（heap）是特殊的數據結構。堆通常是一個可以被看做一棵完全二叉樹(邏輯層面上)的數組對象(物理層面上),常用來在一組變化頻繁(發生增刪查改的頻率較高)的數據中尋找最值.將根結點最大的堆叫做最大堆或大根堆，這樣可以找到堆中的最大值(根節點的值);根結點最小的堆叫做最小堆或小根堆,這樣可以找到堆中的最小值。

其中堆不一定是完全二叉樹，只是為了方便存儲和索引，我們通常用完全二叉樹的形式來表示堆而已。
二叉堆：是一個數組，它可以被看成是一個近似的完全二叉樹。

最大堆，最小堆如圖：
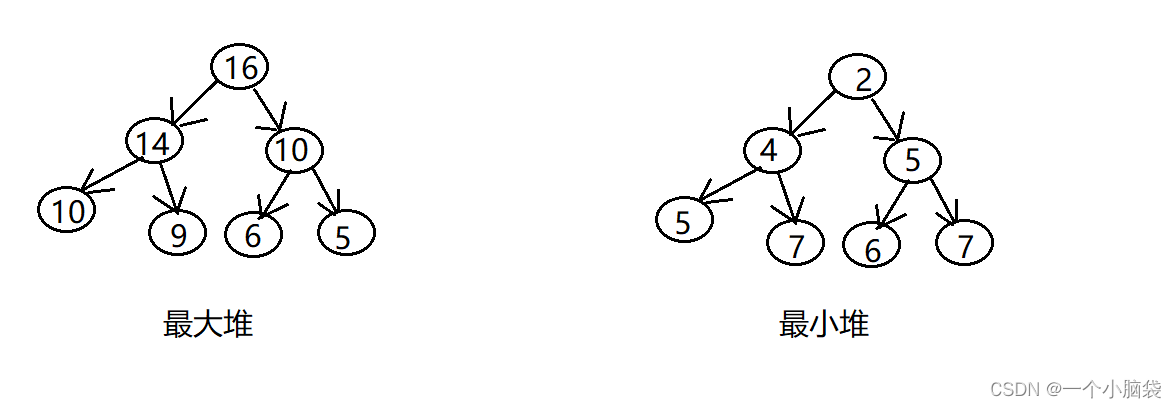
在這里插入圖片描述

最大堆：根結點大于左右子樹結點的值，左右子樹結點的值大于它自己左右子樹結點的值，一種重復下去；最小堆：根結點小于左右子樹結點的值，左右子樹結點的值小于它自己左右子樹結點的值，一種重復下去。

1.2堆的實現

用數組實現一個堆

1.2.1堆的各個接口

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;//動態數組int _size;//存儲數據的下標int _capacity;//動態數組的容量
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的銷毀
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的刪除
void HeapPop(Heap* hp);
// 取堆頂的數據
HPDataTypeHeapTop(Heap* hp);
// 堆的數據個數
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

1.2.2堆的向上調整

//向上調整算法
void HeapJustUp(HPDataType a[], HPDataType child)
{int parsent;parsent = (child - 1) / 2;//找到孩子的父親while (child > 0){int tmp = 0;if (a[parsent] < a[child])//孩子比父親的值大，{tmp = a[child];a[child] = a[parsent];a[parsent] = tmp;}elsebreak;child = parsent;parsent = (parsent - 1) / 2;//找到孩子的父親}
}

對于向上調整，我們把它看做是數組結構，邏輯上看做一顆完全二叉樹。我們只要將要插入堆的數據通過向上調整就可以把它調整成一個大堆。向上調整算法有一個前提：除了要插入的數據，其它的數據已經構成了一個大堆，這樣才能調整。

1.2.3堆的向下調整

void HeapJustDown(Heap* hp)
{//先假設當前待調整結點的左孩子結點存在//并且是待調整結點的左右孩子結點（不管右孩子結點存不存在，都這樣假設）中值最大的int parent = 0;//根節點int child = parent * 2 + 1;//孩子結點while (child < hp->_size){//child+1 < hp->_size說明右孩子結點確實存在//如果hp->_a[child] < hp->_a[child+1]也成立，那說明左右孩子結點中值最大的是右孩子結點if ((child + 1 < hp->_size) && hp->_a[child] < hp->_a[child + 1]){child = child + 1;}//如果a[child]>a[parent],則說明父節點比比左右孩子節點的值都要小，要置換if (hp->_a[child] > hp->_a[parent]){int tmp = hp->_a[parent];hp->_a[parent] = hp->_a[child];hp->_a[child] = tmp;parent = child;child = child * 2 + 1;}//如果a[child] <= a[parent],那就不需要進行調整else{break;}}
}

對于向下調整，我們把它看成是一個數組結構，邏輯上看做一顆完全二叉樹。我們通過從根節點開始的向下調整算法可以把它調整成一個大堆。向下調整算法有一個前提：左右子樹必須是一個堆，才能調整。

1.2.4堆的定義聲明和初始化

1.堆的聲明

typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;//動態數組int _size;//存儲數據的下標int _capacity;//動態數組的容量
}Heap;

創建一個構成動態數組的結構體

2.堆的初始化

// 堆的初始化
void HeapInit(Heap* hp)
{hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (hp->_a == 0){printf("malloc is error\n");exit(-1);}hp->_capacity = 4;hp->_size = 0;
}

開空間，進行初始化

1.2.5堆的數據處理

1.堆的插入

// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{//數據滿了，需要擴容if (hp->_capacity == hp->_size){HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType)*hp->_capacity * 2);if (tmp == NULL){printf("realloc is error");exit(-1);}hp->_a = tmp;hp->_capacity = hp->_capacity * 2;}//不需要擴容hp->_a[hp->_size++] = x;//插入數據，然后_size+1//一般數據都是放到數組尾得，建堆，向上調整，這里我們建大堆HeapJustUp(hp->_a, hp->_size - 1);
}

1.容量不夠就擴容
2.擴容足夠就插入數據
3.然后向上調整建大堆，直到滿足堆

2.堆的刪除

// 堆的刪除，從堆頂開始刪
void HeapPop(Heap* hp)
{
assert(hp);//斷言為空為假的話就報錯
assert(!HeapEmpty(hp));//斷言如果不是空為真就執行
//首元素的的值與尾元素交換，然后刪除尾元素
int tmp = hp->_a[0];
hp->_a[0] = hp->_a[hp->_size - 1];
hp->_a[hp->_size - 1] = tmp;
hp->_size--;
//堆頂元素進行向下調整
HeapJustDown(hp);
}

1.挪動覆蓋刪除堆頂元素，重新建堆
2.盡量保證關系不變（首尾數據交換，再刪除尾部數據，向下調整建堆）

3.獲取堆頂數據

// 取堆頂的數據
HPDataTypeHeapTop(Heap* hp)
{assert(hp->_a);assert(!HeapEmpty(hp));//斷言如果不是空為真就執行return hp->_a[0];
}

堆頂數據就是第一個元素

1.2.6堆的判空和堆的數據個數以及堆銷毀

1.堆的數據個數

// 堆的數據個數
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}

堆的數據個數就是_size的個數

2.堆的判空

// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}

_size為0，說明堆為空

3.堆銷毀

// 堆的銷毀
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}

開一塊空間（malloc），程序結束之前要釋放空間（free）

1.2.7堆的代碼實現

.h頭文件（聲明）

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;//動態數組int _size;//存儲數據的下標int _capacity;//動態數組的容量
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的銷毀
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的刪除
void HeapPop(Heap* hp);
// 取堆頂的數據
HPDataTypeHeapTop(Heap* hp);
// 堆的數據個數
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

.c源文件（定義）

#include "Heap.h"
// 堆的構建
void HeapInit(Heap* hp)
{hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (hp->_a == 0){printf("malloc is error\n");exit(-1);}hp->_capacity = 4;hp->_size = 0;
}
//向上調整算法
HeapJustUp(HPDataType a[], HPDataType child)
{int parsent;parsent = (child - 1) / 2;//找到孩子的父親while (child > 0){int tmp = 0;if (a[parsent] < a[child])//孩子比父親的值大，{tmp = a[child];a[child] = a[parsent];a[parsent] = tmp;}elsebreak;child = parsent;parsent = (parsent - 1) / 2;//找到孩子的父親}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{//數據滿了，需要擴容if (hp->_capacity == hp->_size){HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType)*hp->_capacity * 2);if (tmp == NULL){printf("realloc is error");exit(-1);}hp->_a = tmp;hp->_capacity = hp->_capacity * 2;}//不需要擴容hp->_a[hp->_size++] = x;//插入數據，然后_size+1//一般數據都是放到數組尾得，建堆，向上調整，這里我們建大堆HeapJustUp(hp->_a, hp->_size - 1);
}
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->_size == 0;
}
//堆頂元素進行向下調整
void HeapJustDown(Heap* hp)
{//先假設當前待調整結點的左孩子結點存在//并且是待調整結點的左右孩子結點（不管右孩子結點存不存在，都這樣假設）中值最大的int parent = 0;//根節點int child = parent * 2 + 1;//孩子結點while (child < hp->_size){//child+1 < hp->_size說明右孩子結點確實存在//如果hp->_a[child] < hp->_a[child+1]也成立，那說明左右孩子結點中值最大的是右孩子結點if ((child + 1 < hp->_size) && hp->_a[child] < hp->_a[child + 1]){child = child + 1;}//如果a[child]>a[parent],則說明父節點比比左右孩子節點的值都要小，要置換if (hp->_a[child] > hp->_a[parent]){int tmp = hp->_a[parent];hp->_a[parent] = hp->_a[child];hp->_a[child] = tmp;parent = child;child = child * 2 + 1;}//如果a[child] <= a[parent],那就不需要進行調整else{break;}}
}
// 堆的刪除，從堆頂開始刪
void HeapPop(Heap* hp)
{
assert(hp);//斷言為空為假的話就報錯
assert(!HeapEmpty(hp));//斷言如果不是空為真就執行
//首元素的的值與尾元素交換，然后刪除尾元素
int tmp = hp->_a[0];
hp->_a[0] = hp->_a[hp->_size - 1];
hp->_a[hp->_size - 1] = tmp;
hp->_size--;
//堆頂元素進行向下調整
HeapJustDown(hp);
}
// 取堆頂的數據
HPDataTypeHeapTop(Heap* hp)
{assert(hp->_a);assert(!HeapEmpty(hp));//斷言如果不是空為真就執行return hp->_a[0];
}
// 堆的數據個數
int HeapSize(Heap* hp)
{assert(hp);return hp->_size;
}
// 堆的銷毀
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_capacity = hp->_size = 0;
}

.c源文件（測試）

#include "Heap.h"
int main()
{Heap hp;HeapInit(&hp);//初始化HeapPush(&hp, 2);//插入數據HeapPush(&hp, 3);HeapPush(&hp, 4);HeapPush(&hp, 5);HeapPush(&hp, 6);HeapPush(&hp, 1);HeapPush(&hp, 66);HeapPush(&hp, 62);HeapPush(&hp, 4);HeapPush(&hp, 6);HeapPop(&hp);//刪除數據,從堆頂開始刪int tmp= HPDataTypeHeapTop(&hp);//取堆頂元素// 堆的數據個數int num = HeapSize(&hp);printf("建大堆，棧頂元素為：%d,堆的數據個數：%d\n", tmp,num);for (int i = 0; i < num; i++)printf("%d ", hp._a[i]);HeapDestory(&hp);// 堆的銷毀return 0;
}

二、TOP—K問題

TOP—K問題：求數據集合中前k個最大的元素和最小的元素，一般情況數據非常大。
如：專業前10，世界500強，游戲中前100的活躍玩家，各種榜單等等。

1.用數據集合中前k個元素來建堆
求前k個最大的元素，建小堆
求前k個最小的元素，建大堆
2.用剩余的N—K個元素依次與堆頂元素來比較，根據規則替換堆頂元素，N—K個元素依次與堆頂元素比較完成后，堆里的K個元素就是所求的最小或者最大的元素。

例子：

問題：假設1億個數，內存存不下，數據在文件中找出最大的前k個數。
1.讀取文件的前10個數據，在內存數組中建立一個小堆。
2.在依次讀取剩下數據，跟堆頂元素比較，大于堆頂的數據就替換它，然后向下調整。
3.所有數據讀完，堆里面數據就是最大的前10個數。

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define n 100000000
void  WeinteData()//寫入1億數據
{FILE* fp = fopen("top.txt", "w");//打開文件，只寫
if (fp == NULL)
{perror("fopen error");exit(-1);
}
srand((unsigned)time(0));
int arr[100] = { 0 };
for (int i = 0; i < n; i++)
{int x = rand() % 10000 + 1;fprintf(fp, "%d\n", x);
}
fclose(fp);//關閉文件
}
//兩個數交換
void Swap(int* p, int* q)
{int tmp;tmp = *q;*q = *p;*p = tmp;
}
//向下調整算法
void JustDown(int* arr,int k,int parent)
{int child = parent * 2 + 1;//左孩子結點while (child < k){if ((child + 1 < k) && arr[child] > arr[child + 1])//找到最小值的孩子結點child += 1;//如果arr[child]<arr[parent],則說明父節點比比左右孩子節點的值都要大，要置換if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);//讓孩子結點為父節點，并且更新它的兒子結點parent = child;child = child * 2 + 1;}//如果a[child] <= a[parent],那就不需要進行調整else{break;}}
}
//建小堆
void HeapCreate(int* arr,int k)
{//最后一個結點的父親結點開始向下調整for (int i = (k - 2) / 2; i >= 0; --i){//向下調整算法JustDown(arr, k, i);}
}
void  FileTakeK()
{int k = 10;//10個數int* a = (int*)malloc(sizeof(int) * k);//開辟一塊空間用來建堆if (a == NULL){perror("malloc error:");exit(-1);}FILE* file = fopen("top.txt", "r");//打開top.txt文件,只讀模式if (file == NULL){perror("fopen error:");exit(-1);}for (int i = 0; i < k; i++){fscanf(file, "%d", &a[i]);}printf("前10個數:\n");for (int i = 0; i < k; i++)printf("%d ", a[i]);//建小堆HeapCreate(a, k);printf("\n建完小堆里面的數:\n");for (int i = 0; i < k; i++)printf("%d ", a[i]);//把剩余的n-k個數與小堆的堆頂比較，比較完成后，堆里的數就是文件里最大的10個數int x = 0;while (fscanf(file, "%d", &x) != EOF){//比堆頂數大，把這個數賦值給堆頂，然后向下調整if (x > a[0])a[0] = x;JustDown(a, k, 0);}printf("\n取最大的10個數:\n");for (int i = 0; i < k; i++)printf("%d ", a[i]);free(a);//釋放內存fclose(file);//關閉文件
}
int main()
{//寫入1億數據WeinteData();//從文件中取出k個數,建小堆FileTakeK();return 0;
}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/168139.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/168139.shtml
英文地址，請注明出處：http://en.pswp.cn/news/168139.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

C++ 文件和流、異常處理、動態內存、預處理器

C++ 文件和流、異常處理、動態內存、預處理器

一、C文件和流&#xff1a; 在C中進行文件處理&#xff0c;需要包含頭文件<iostream>和<fstream>。fstream標準庫定義的三個新的數據類型&#xff1a; 數據類型 描述 ofstream 該數據類型表示輸出文件流&#xff0c;用于創建文件并向文件寫入信息。 ifstream …
閱讀更多...
vscode項目推送到git

vscode項目推送到git

1、打開項目文件 打開文件后點擊vs code左側工具欄中第三個源代碼管理圖標&#xff0c;點擊初始化倉庫&#xff0c;此時會創建一個本地倉庫會檢查該項目中的文件變更 2、創建遠程倉庫 點擊克隆/下載&#xff0c;復制HTTPS地址 3、添加遠程地址 1&#xff09;圖形化操作 2…
閱讀更多...
Leetcode刷題之用隊列實現棧（C語言版）

Leetcode刷題之用隊列實現棧（C語言版）

Leetcode刷題之用隊列實現棧&#xff08;C語言版&#xff09; 一、題目描述二、題目要求三、題目示例四、題目解析Ⅰ、MyStack* myStackCreateⅡ、void myStackPush(MyStack* obj, int x)Ⅲ、int myStackPop(MyStack* obj)Ⅳ、int myStackTop(MyStack* obj)Ⅴ、bool myStackEmp…
閱讀更多...
文件夾重命名：徹底擺脫數字困擾，批量修改文件夾名去除數字

文件夾重命名：徹底擺脫數字困擾，批量修改文件夾名去除數字

在日常生活和工作中&#xff0c;經常會遇到需要修改文件夾名稱的情況。有時候是因為文件夾名稱中包含了數字&#xff0c;有時候是因為文件夾名稱不符合規范。無論出于什么原因&#xff0c;修改文件夾名稱都是一件非常繁瑣的事情。尤其是需要修改大量文件夾名稱時&#xff0c;手…
閱讀更多...
Jenkins 整合 Docker 自動化部署

Jenkins 整合 Docker 自動化部署

Docker 安裝 Jenkins 配置自動化部署 1. Docker 安裝 Jenkins 1.1 拉取鏡像文件 docker pull jenkins/jenkins1.2 創建掛載文件目錄 mkdir -p $HOME/jenkins_home1.3 啟動容器 docker run -d -p 8080:8080 -v $HOME/jenkins_home:/var/jenkins_home --name jenkins jenkin…
閱讀更多...
CentOS rpm安裝Nginx和配置

CentOS rpm安裝Nginx和配置

CentOS rpm安裝Nginx和配置 官方下載地址: http://nginx.org/en/download.html 介紹 Nginx(“engine x”)是一款由俄羅斯的程序設計師Igor Sysoev所開發高性能的 Web和 反向代理 服務器&#xff0c;也是一個 IMAP/POP3/SMTP 代理服務器。 rpm包安裝 #安裝nginx&#xff0c…
閱讀更多...
k8s部署的java服務查看連接nacos緩存的配置文件

k8s部署的java服務查看連接nacos緩存的配置文件

一、問題描述 k8s部署的java服務&#xff0c;使用nacos中的配置文件&#xff0c;需要在緩存中查看該服務具體是使用到了哪些配置文件 二、解決 參考文檔: https://nacos.io/zh-cn/docs/system-configurations.html 文檔描述如下: 進入java服務容器進入用戶目錄下的nacos&a…
閱讀更多...
4-Docker命令之docker version

4-Docker命令之docker version

1.docker version介紹 docker version命令是用于查看docker容器的版本信息 2.docker version用法 docker version [參數] [root@centos79 ~]# docker version --helpUsage: docker version [OPTIONS]Show the Docker version informationOptions:-f, --format string Fo…
閱讀更多...
Android 12.0 mt6771新增分區功能實現四

Android 12.0 mt6771新增分區功能實現四

1.前言 在12.0的系統rom開發中，在對某些特殊模塊中關于數據的存儲方面等需要新增分區來保存， 所以就需要在系統分區新增分區，接下來就來實現這個功能，看第四部分的新增分區的實現過程 2.mt6771新增分區功能實現四的核心類 device/mediatek/mt6771/ueventd.mt6771.rcdevice…
閱讀更多...
Java枚舉詳解

Java枚舉詳解

一、什么是枚舉類型 枚舉類型是一種特殊的數據類型&#xff0c;用于定義一組固定的命名常量。枚舉類型提供了一種更強大、更安全和更易讀的方式來表示一組相關的常量。 在Java中&#xff0c;枚舉類型是通過使用enum關鍵字來定義的。枚舉類型可以包含一個或多個枚舉常量&#xf…
閱讀更多...
常見狀態碼總結

常見狀態碼總結

常見狀態碼總結 2xx 200 OK&#xff1a;表示服務器成功處理了客戶端的請求&#xff0c;并返回所請求的數據。這是最常見的狀態碼&#xff0c;表示一切正常。201 Created&#xff1a;表示服務器成功處理了客戶端的 POST 請求&#xff0c;并在服務器上創建了新的資源。204 No C…
閱讀更多...
vue005——vue組件入門（非單文件組件和單文件組件）

vue005——vue組件入門（非單文件組件和單文件組件）

一、非單文件組件 1.1、單文件組件的使用 1.1.1、局部注冊 1、第一步&#xff1a;創建school組件 2、第二步&#xff1a;注冊組件&#xff08;局部注冊&#xff09; 3、第三步&#xff1a;使用組件&#xff08;編寫組件標簽&#xff09; <!DOCTYPE html> <html>…
閱讀更多...
設計模式—里氏替換原則

設計模式—里氏替換原則

1.概念 里氏代換原則(Liskov Substitution Principle LSP)面向對象設計的基本原則之一。 里氏代換原則中說&#xff0c;任何基類可以出現的地方&#xff0c;子類一定可以出現。 LSP是繼承復用的基石&#xff0c;只有當衍生類可以替換掉基類&#xff0c;軟件單位的功能不受到影…
閱讀更多...
Spring注解方式整合第三方框架

Spring注解方式整合第三方框架

目錄 Spring整合MyBatis 原有xml方式整合配置如下 注解方式&#xff1a; Import可以導入如下三種類 第三方框架是指由其他開發者或團隊開發的軟件模塊或庫&#xff0c;供開發者在自己的應用程序中使用。這些框架通常提供了一系列已經封裝好的功能或工具&#xff0c;可節省開…
閱讀更多...
使用flask返回json格式的數據

使用flask返回json格式的數據

Flask Flask是一個使用Python編寫的輕量級Web框架&#xff0c;它的設計理念是保持簡單、靈活和易擴展。它的核心是Werkzeug和Jinja2&#xff0c;并且它本身只提供了非常基礎的Web框架功能&#xff0c;例如路由和請求處理等。 使用Flask可以快速創建一個Web應用程序&#xff0c;…
閱讀更多...
跳躍游戲Ⅱ[中等]

跳躍游戲Ⅱ[中等]

優質博文&#xff1a;IT-BLOG-CN 一、題目 給定一個長度為n的0索引整數數組nums。初始位置為nums[0]。每個元素nums[i]表示從索引i向前跳轉的最大長度。換句話說&#xff0c;如果你在nums[i]處&#xff0c;你可以跳轉到任意nums[i j]處: 0 < j < nums[i] i j < n …
閱讀更多...
【Python 訓練營】N_8 打印阿姆斯特朗數

【Python 訓練營】N_8 打印阿姆斯特朗數

題目 輸入一個數&#xff0c;判斷是否為阿姆斯特朗數&#xff0c;阿姆斯特朗數指一個n位正整數等于其各位數字的n次方之和。其中n為3時是水仙花數。 分析 利用循環&#xff0c;獲取數的長度&#xff0c;根據長度和定義&#xff0c;拆分出來運算 答案 while True:n int(in…
閱讀更多...
【Python 訓練營】N_7 打印水仙花數

【Python 訓練營】N_7 打印水仙花數

題目 打印出1000以內所有的"水仙花數"&#xff0c;所謂"水仙花數"是指一個三位數&#xff0c;其各位數字立方和等于該數本身。例如&#xff1a;153是一個"水仙花數"&#xff0c;因為1531的三次方&#xff0b;5的三次方&#xff0b;3的三次方。 …
閱讀更多...
數學啟發式

數學啟發式

學習資料&#xff1a; 優化求解器 | Gurobi 數學啟發式算法&#xff1a;參數類型與案例實現 數學啟發式算法 | 可行性泵 (Feasibility Pump)算法精講&#xff1a;一份讓您滿意的【理論介紹編程實現數值實驗】學習筆記(PythonGurobi實現) 大佬到底是大佬&#xff01;這些資料太…
閱讀更多...
Mac Ubuntu雙系統解決WiFi和WiFi 5G網絡不可用問題

Mac Ubuntu雙系統解決WiFi和WiFi 5G網絡不可用問題

文章目錄 設備信息1. Ubuntu WiFi不可用解決方式查看Mac的網卡型號根據網卡型號搜索獲取到的解決方法查看WiFi名字問題參考鏈接 2. 解決WiFi重啟后失效問題打開終端創建.sh腳本文件編輯腳本文件復制粘貼腳本修改腳本權限創建并編輯systemd service文件復制粘貼下文到systemd se…
閱讀更多...
最新文章

Copyright @ 2022~2023