665. 非遞減數列
題解:
題目要求一個非遞減數列,我們可以考慮需要更改的情況:
- nums = {4, 2, 5}
對于這個nums,由于2的出現導致非遞減,更改的情況就是要么4調到<=2,要么2調到4,5.
- nums = {1, 4, 2, 5}
對于這個nums,由于2的出現導致非遞減,更改的情況就是要么4調到1,,2,要么2調到4,5.
- nums = {3, 4, 2, 5}
對于這個nums,由于2的出現導致非遞減,更改的情況就是2調到4,5.
所以算法就是:
如果按照1的情況,當i = 1,那么直接就把nums[i - 1]改成nums[i],nums[i]不動
如果按照2的情況,當nums[i - 2] < nums[i],那我們就優先考慮把nums[i - 1]?調小到?>= nums[i - 2] 并且 <= nums[i]
如果按照1的情況,nums[i - 2] > nums[i],那我們就調整nums[i],讓nums[i] = nums[i - 1]。
代碼:
class Solution {public boolean checkPossibility(int[] nums) {int count = 0;//統計需要滿足非遞減的次數for(int i = 1; i < nums.length;i++){if(nums[i] < nums[i - 1]){if(i == 1 || nums[i] >= nums[i - 2]){// i=1就是第一個情況,后面的是第二種nums[i - 1] = nums[i];}else{nums[i] = nums[i - 1];}count++;}}return count <= 1;}
}453. 最小移動次數使數組元素相等
思路:
題目要求我們每次操作將會讓n-1個元素增加1,來滿足要求。我們可以反過來思考,找到最小的數,遍歷其他的數,累加所有元素和最小的元素的差距。
代碼:
class Solution {public int minMoves(int[] nums) {int minNum = Arrays.stream(nums).min().getAsInt();int res = 0;for(int num : nums){res += num - minNum;}return res;}
}283. 移動零
思路:(雙指針)
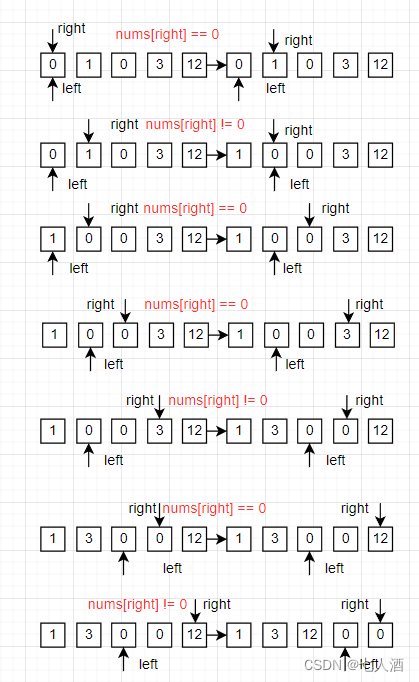
我們定義兩個指針left, right都等于0,遍歷nums,如果nums[right] != 0,那我們就讓nums[left]和nums[right]進行交換,再把Left增加。如果等于0,那就讓right++。
其實Left就是第一個0的位置,right就是讓他找到不為0的地方。
189. 旋轉數組
思路:
- 第一步:先翻轉數組里的數
- 第二步:翻轉前[0, k - 1]個數
- 第三步:翻轉后面[k, n]的數
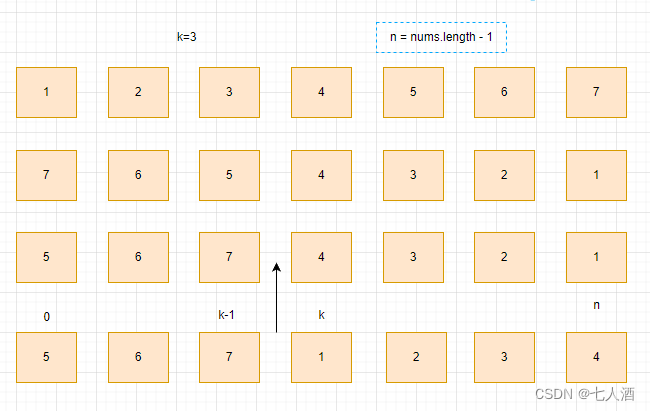
代碼:
class Solution {public void rotate(int[] nums, int k) {k %= nums.length;reverse(nums, 0, nums.length - 1);reverse(nums, 0, k - 1);reverse(nums, k, nums.length - 1);}public void reverse(int[] nums, int left, int right){while(left <= right){int temp = nums[left];nums[left] = nums[right];nums[right] = temp;left++;right--;}}
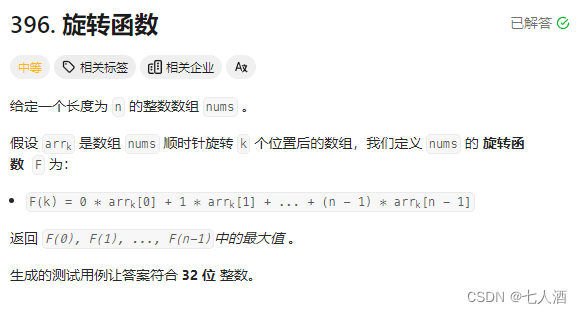
}396. 旋轉函數
思路:
找規律
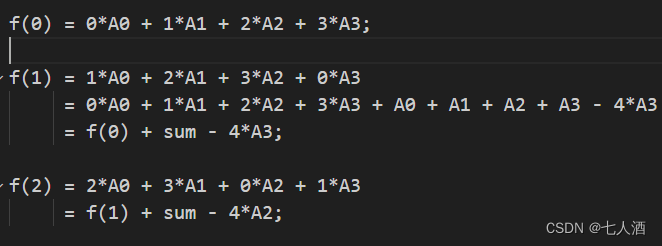
所以對應的公式:
代碼:
class Solution {public int maxRotateFunction(int[] nums) {int sum = 0, f = 0, n = nums.length, ans = 0;for(int i = 0; i < n; i++){sum += nums[i];f += i * nums[i];//f(0);}ans = f;for(int i = 1; i < n; i++){f = f + sum - n * (nums[n - i]);//f[i] = f[i - 1] + sum -n * nums[n - i];ans = Math.max(ans, f);}return ans;}
}













)






