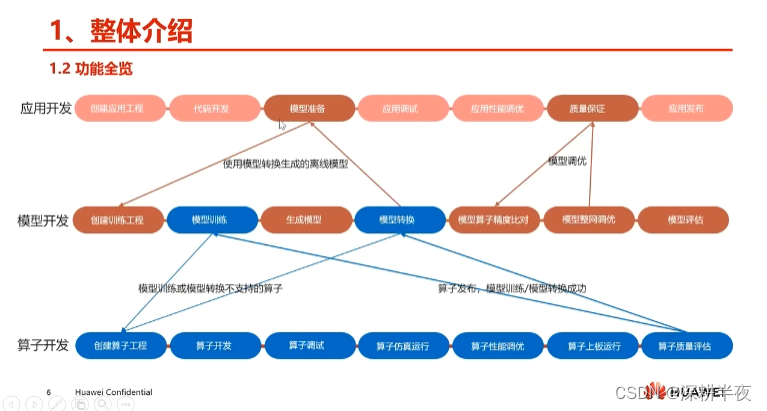
?一場景介紹

二 安裝介紹

1.LINUX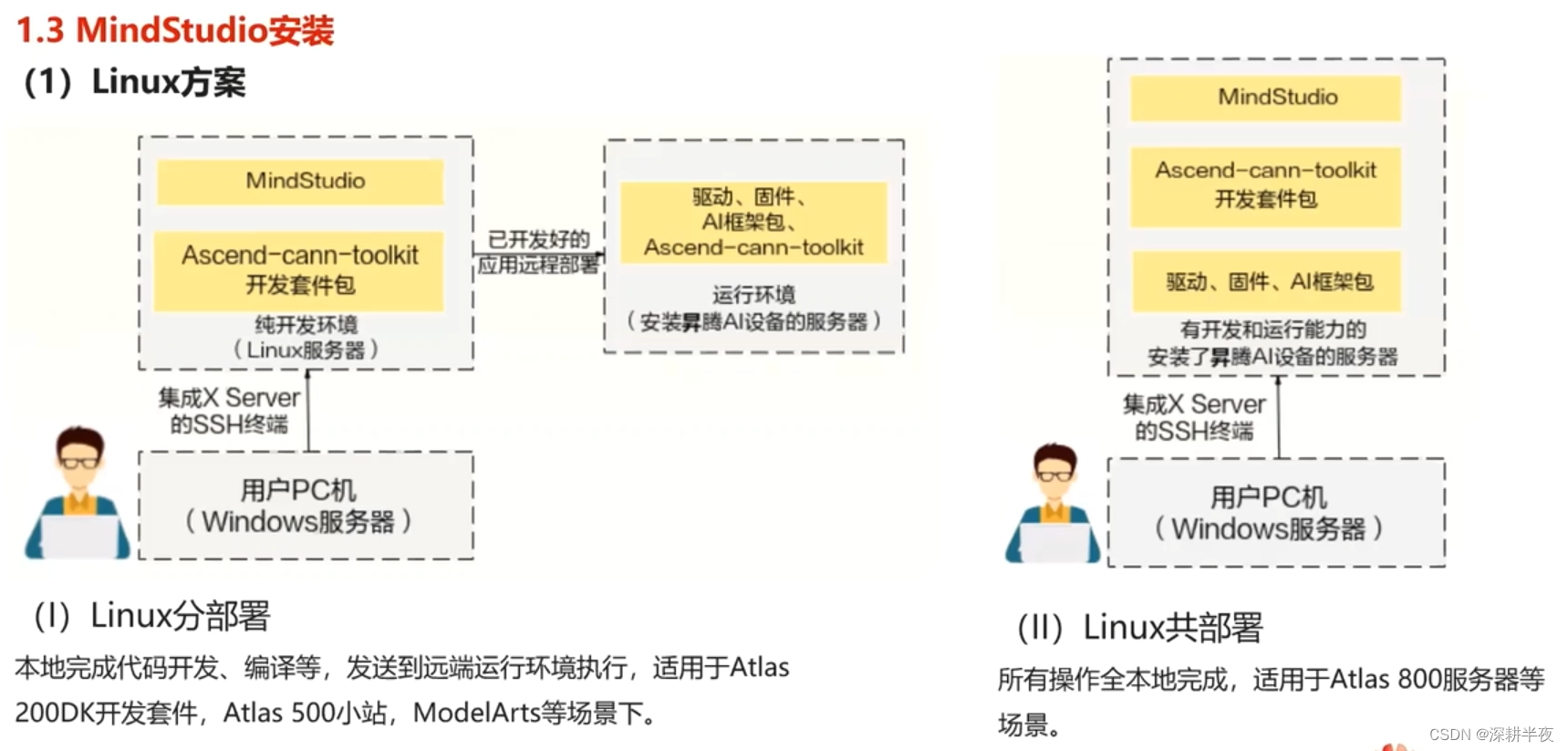

采用無昇騰硬件采用linux 分部署? ? ??

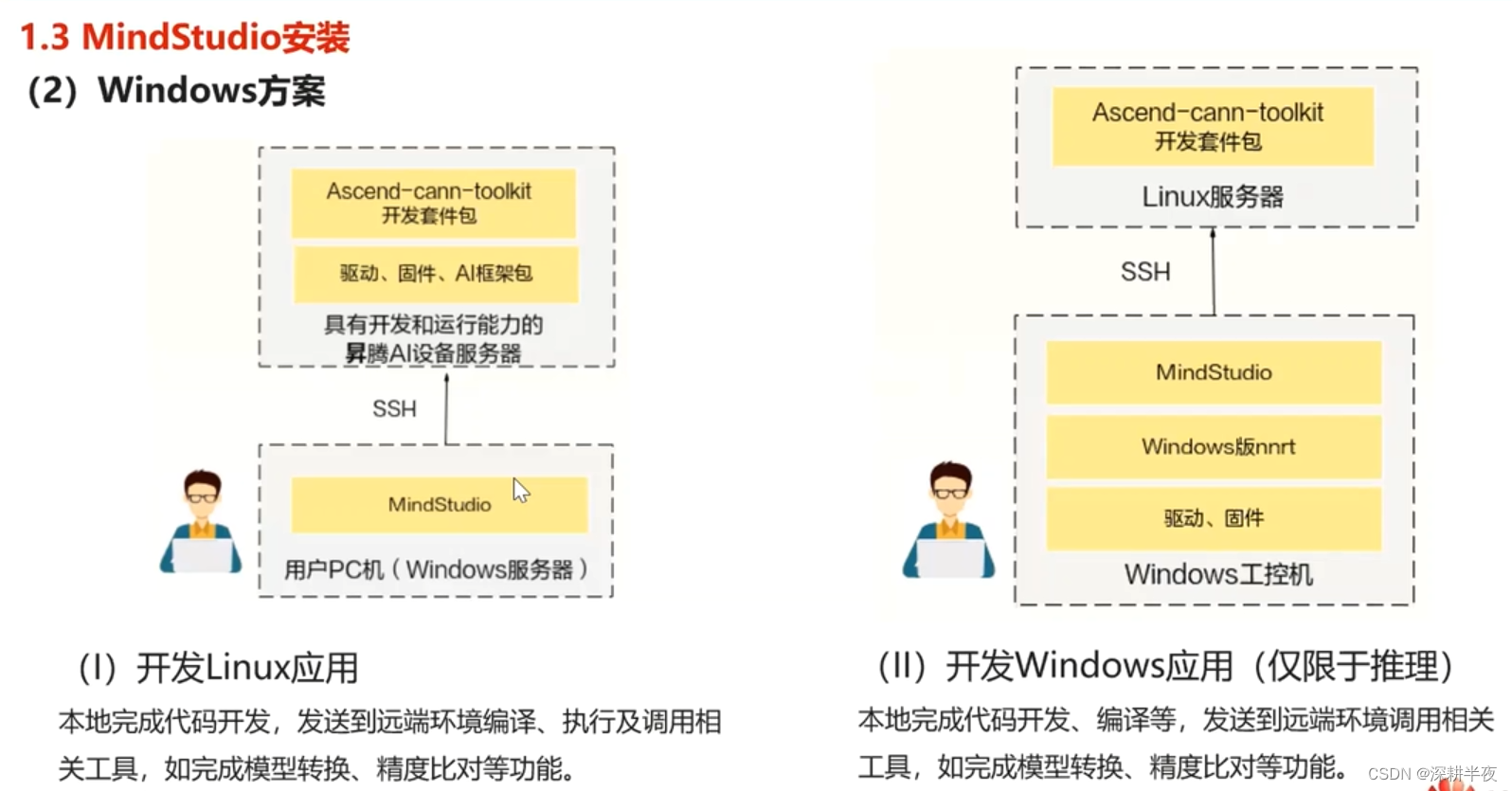
2.WINDOWS

3.linux下安裝整體步驟

3.1安裝依賴

3.2?安裝步驟

1.gcc cmake 等依賴

2.python3.7.5

3.pip 安裝依賴

4.安裝JDK

5.安裝 Ascend-cann-toolkit

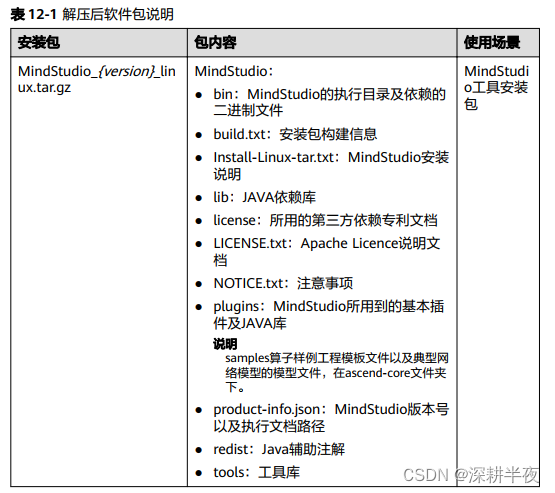
?6.解壓安裝Mindstudio

?7.進入bin路徑 ./Mindstudio 執行啟動

昇騰全流程開發工具鏈（MindStudio）-昇騰社區 (hiascend.com)