LCR 079. 子集 - 力扣（LeetCode）
方法一?
1. 決策樹：對于決策樹，思考的角度不同，畫出的決策樹也會不同，這道題可以從兩個角度來畫決策樹。
2. 考慮全局變量的使用：
使用全局變量 List<List<Integer>> ret 來存子集；
使用全局變量?List<Integer>?path 來存遞歸過程中的值；
3. 關注遞歸本身，回溯，剪枝，遞歸出口：
1. 遞歸本身：使用方法 dfs(nums，i)，nums為參數數組，i 表示當前進行選擇或者不選擇的目標數是 nums[i]，當選擇目標數的時候，path + nums[i] 然后遞歸下一輪，不選擇的時候，直接遞歸下一輪，dfs(nums，i+1)；
2. 剪枝：從決策樹可以看出，這道題是不需要到剪枝環節的；
3. 回溯：當決策樹中的節點對目標數進行判斷完成后，需要進行 "恢復現場" 操作，也就是需要將當前的全局變量 path 的最后一個元素去掉，從而恢復現場，可以按下圖來理解；
4. 遞歸出口：當 dfs(nums,i) 中 i 的值 == nums.size 的時候，說明已經超出數組的范圍了，此時就可以返回了；
代碼實現?
class Solution {List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums,0);return ret;}public void dfs(int[] nums,int i){// 遞歸出口if(i == nums.length){ret.add(new ArrayList(path));return;}// 選path.add(nums[i]);dfs(nums,i+1);// 回溯，恢復現場path.remove(path.size()-1);// 不選dfs(nums,i+1);}
}方法二?
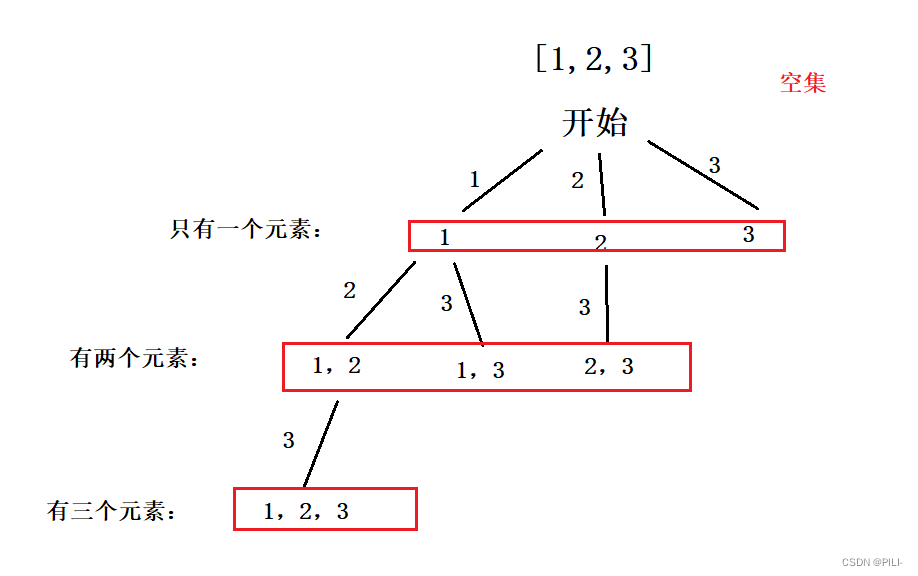
?第二種決策樹：這種思考方式，就是從選擇多少個元素來考慮，但要求的是從數組 i 定位從小到大進行選擇，在選擇完前 n 個元素后，繼續選擇 n+1 個元素時，只能是選擇當前 i 之后對應的元素，也就是數組 [1,2,3] 當選擇到 2 的時候，再進行選擇時，就只能選 3 了，不能選 1 ，這樣是為了避免重復情況出現；
2. 全局變量的使用與第一種方法一樣；?
3. 關注遞歸本身，回溯，剪枝，遞歸出口：
1. 觀察決策樹，可以發現每一個節點都作為子集，也就是每次進入都可以作為一個結果然后存進全局變量 ret 中；
2. dfs(nums[]，i) 此處的 i 可以理解為當前的 path 要從 i 開始進行選擇；
3. 跟第一種情況相同，不需要進行剪枝；
4. 回溯也跟第一種情況相同，將最后一個元素去掉；
5. 并且要注意，在這種情況下，是沒有遞歸出口的，因為每個節點都作為子集，在 for 循環中循環結束后就會自動返回；
代碼實現?
class Solution {List<List<Integer>> ret;List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums,0);return ret;}public void dfs(int[] nums,int i){// 每個節點都是子集，進入就添加到 ret 中ret.add(new ArrayList(path));for(int j=i;j<nums.length;j++){ // 從節點 i 開始path.add(nums[j]);dfs(nums,j+1); // 回溯，恢復現場path.remove(path.size()-1);}}
}
)
