每日一題系列（day 03）

前言：

🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈

?? 🔎🔎如果說代碼有靈魂，那么它的靈魂一定是👉👉算法👈👈，因此，想要寫出💚優美的程序💚，核心算法是必不可少的，少年，你渴望力量嗎😆😆，想掌握程序的靈魂嗎???那么就必須踏上這樣一條漫長的道路🏇🏇，我們要做的，就是斬妖除魔💥💥，打怪升級！💪💪當然切記不可😈走火入魔😈，每日打怪，日日累積，終能成圣🙏🙏！開啟我們今天的斬妖之旅吧！????

LeetCode-102.二叉樹的層序遍歷

題目：

給你二叉樹的根節點 root ，返回其節點值的 層序遍歷 。 （即逐層地，從左到右訪問所有節點）。

示例1：

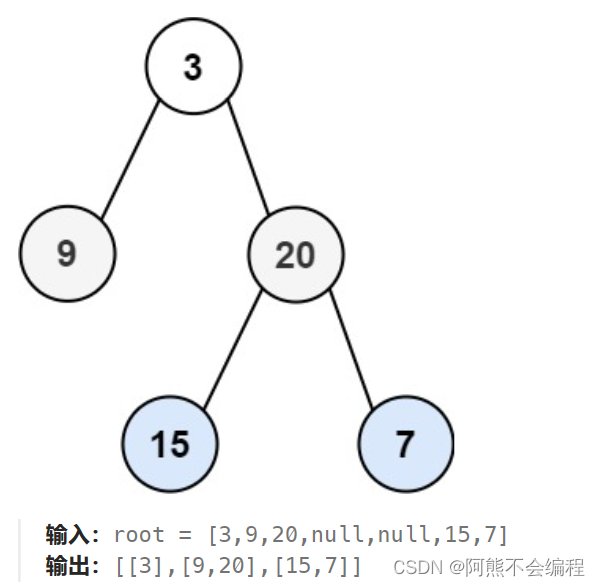
示例2：

注意事項：

• 樹中節點數目在范圍 [0, 2000] 內
• -1000 <= Node.val <= 1000

---

解法一：

??思路：

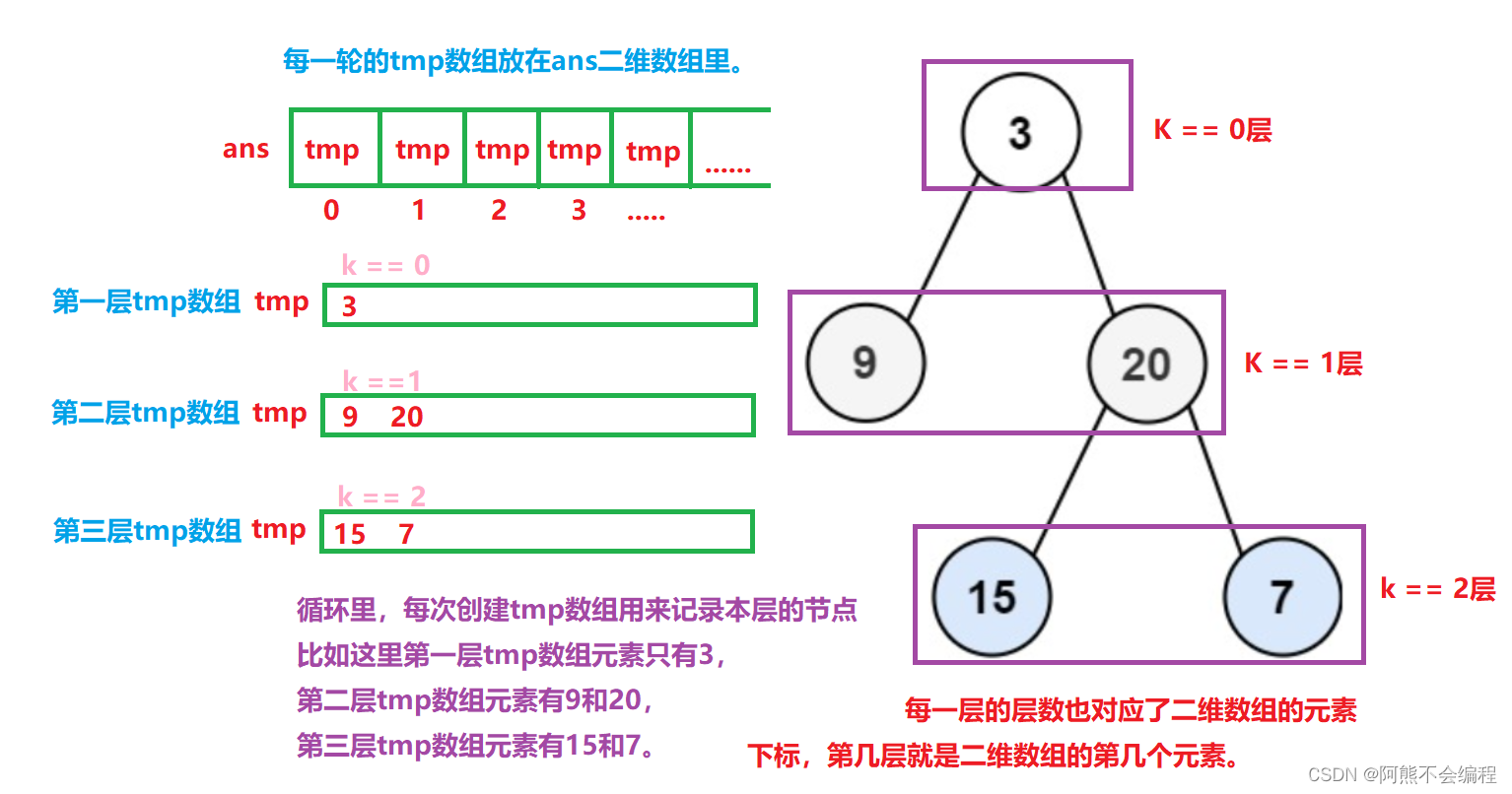
??說到二叉樹的層序遍歷，我們第一反應肯定是用廣度優先搜索，廣搜需要隊列存儲每一層的節點，當一層節點處理完之后再將本層已處理的節點全部pop掉，接著處理下一層節點，直到處理完畢，深搜便完成了，這里題目要求用二維數組來接收深搜的結果，所以我們可以開個二維數組，在每層節點pop之前，把每層節點記錄在一位數組中，最終把一維數組放到二維數組中。每一層的二維數組都代表每一層的節點的遍歷結果。

??1、首先，當節點為空的時候我們直接返回空的二維數組。不為空則根據題目要求創建一個二維數組，再創建隊列來記錄二叉樹的每個節點，再將根節點壓入到隊列中。
??2、節點已經入隊，開始處理二叉樹。我們知道，二叉樹有很多層，所以我們需要一層一層來遍歷，每一層處理完后，本層節點也被pop，再處理下一層，其實這就是一個循環的過程。條件是只要不為空就一直處理。
??3、在循環內，創建一個臨時一維數組來記錄本層所有節點的值，用計數器來記錄這層擁有的節點個數，再使用for循環處理每一層的節點。
??4、for循環內，取隊頭元素，將隊頭的元素值壓入本層的一維數組中，當處理的當前節點時，如果當前節點有子節點，就把下一層的子節點入隊，用來下次的遍歷，最后再將當前已經處理完了的節點pop出隊列。
??5、最后直接返回二維數組即可。

代碼實現：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if(root == NULL)vector<vector<int>> ans;//根據題目要求創建一個二維數組return vector<vector<int>>();//節點為空直接返回空的二維數組即可queue<TreeNode *> q;//創建一個隊列用來記錄每一層的節點TreeNode *node = nullptr;//記錄隊列的每個節點，便于處理單個節點q.push(root);//將根節點壓入隊列while(!q.empty())//只要隊列不為空說明這一層還存在節點{int cnt = q.size();//記錄隊列節點數量vector<int> tmp;//使用tmp數組接收每一層的節點for(int i = 0 ; i < cnt ; i++)//處理每層的節點{node = q.front();//記錄取隊頭節點tmp.push_back(node -> val);//在隊列這層節點pop之前將節點值壓入本層的一維數組，這個一維數組就是這層節點if(node -> left) q.push(node -> left);//本層節點的左子樹存在就把左孩子入隊列，下次處理if(node -> right) q.push(node -> right);//本層節點的右子樹存在就把右孩子入隊列，下次處理q.pop();//本層節點處理完，把本層pop掉，處理下一層節點}ans.push_back(tmp);//將一維數組（本層遍歷結果）尾插進二維數組}return ans;//返回二維數組即可}
};

---

解法二：

??思路：

??其實這題完全可以不用廣搜，使用深搜也能進行層序遍歷，并且使用深搜的代碼會更加簡潔一些。使用深搜也就是dfs，那么如何深搜才是關鍵，其實我們只需要知道每個節點的層數就可以進行深搜了，我們可以直接用節點的層數把深搜的每個節點壓入到對應層的數組中。

??1、在深度優先搜索前，我們按照題目要求先創建一個二維數組，然后進行深搜，這里需要注意，dfs的參數首先要傳入根節點，在傳入從哪層開始處理的層次（從第0層開始處理），最后再傳參二維數組的引用。
??2、進入到深搜，如果節點為空的話直接返回。當本層層數與二維數組存儲的一維數組數量相等，表示已經處理到當前的層數了，這個時候在二維數組當前層數（下標）插入一個空一維數組。
??3、接下來就將每一層的節點插入到對應層的一維數組中，然后向左子樹搜索，左子樹為當前層的下一層，所以傳參k + 1，然后向右子樹搜索，同樣層數為k + 1，最后return即可。

代碼實現：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void dfs(TreeNode *root, int k, vector<vector<int>> &ans)//傳參需要根節點，節點所在層數，以及二維數組的引用傳參{if(root == NULL) return;//根節點為null直接返回if(k == ans.size()) ans.push_back(vector<int>());//當當前層數與二維數組存儲一維數組數量相同時，表示處理到當前的層數了，對二維數組進行尾插一個空一維數組ans[k].push_back(root -> val);//將每一層的節點尾插到每一層的數組里dfs(root -> left,  k + 1, ans);//深搜左子樹，下一層節點層數要加一dfs(root -> right, k + 1, ans);//同樣，深搜下一層右子樹，層數加一return;//深搜結束}vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> ans;//創建二維數組dfs(root, 0, ans);//進行深搜return ans;//返回深搜結果即可}
};

---

??二叉樹的層序遍歷，我們通常是使用第一種隊列的方式進行廣度優先搜索，然而用深度優先搜索來對二叉樹層序遍歷的代碼設計感更優美，可讀性也更高。