400.給你一個整數 n ，請你在無限的整數序列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …] 中找出并返回第 n 位上的數字。
示例 1：
輸入：n = 3
輸出：3
示例 2：
輸入：n = 11
輸出：0
解釋：第 11 位數字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, … 里是 0 ，它是 10 的一部分。

• 最開始 n 對應的就是 n，但是當數字成為兩位數之后就開始對不上了，所以能想到這題的關鍵在于隨著數字位數的變化，如何找到 n 對應的結果，為了方便稱呼先定義幾個概念：
• 位數(digit)：這個數字有幾位，比如兩位數，三位數
• 數位：比如數字 10，11，12 組成的序列 101112，其中每一位都是一個數位，其實也就是題目所說的序列上的某一位
• 數字(num)，比如 10，11，12 ，這三個數都是數字
• 起始數字(start)：某位數最小的數字，比如兩位數的范圍是 10~99，start 就是 10
• 數位數量(count)：只算 n 位數包含的數位數量，比如兩位數為 10~99 ，有 90 個 兩位數(每個數的數位數量為 2)，所以位數數量為 90 * 2 = 180
• 現在我們知道關鍵在于位數變化，所以研究位數變化帶來的一些規律
  
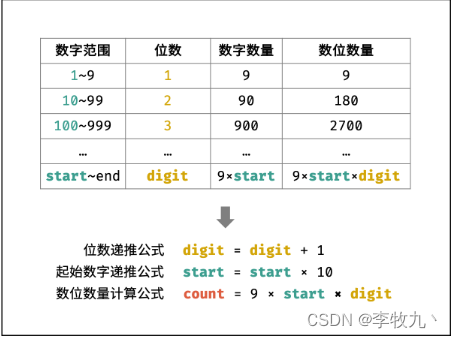
• 位數遞推公式：觀察從一位數，兩位數，三位數的變化，所以 digit(i+1) = digit(i) + 1
• 起始數字遞推公式：最小一位數為 1，最小兩位數為 10…所以 start(i+1) = start(i) * 10
• 數位數量計算公式：n 位數范圍內的數位數量總和，比如一位數包含了 9 個 一位數，所以為 9*1；兩位數包含了 90 個 兩位數，所以為 90*2；三位數包含 900 個三位數所以為 900*3，所以規律其實就是 count = 9 * start * digit
• 接下來我們第一步先確定 n 對應的數是幾位數，其實 n 對應的是數位數量，所以我們就讓 n 不斷減去 count，直到 n <= count，就能得到 n 對應幾位數。
• 第二步我們確定一下他對應具體數字 num 為什么，將第一步計算完剩下的 n 整除 digit ，再加上起始值 start 就知道它對應哪個數，但是其實我們的推導過程都沒去管 0 這個數，它也算一個數位，所以實際上 num 應該是 start + (n-1)/digit;
• 確定完了 num，同理還是用 n-1，讓它對 digit 取余我們就知道他在這個數的第幾位，所以把 num 轉為 string，num.charAt((n-1)%digit) 就是最終對應的字符，轉為數字即為最終結果

•   public int findNthDigit(int n) {long start = 1;int digit = 1;long count = 9;// 第一步while(n > count){n -= count;start*=10;digit++;count = start * digit * 9;}// 第二步long num = start + (n-1)/digit;// 第三步return Long.toString(num).charAt((n-1)%digit) - '0';}
  

• 這是從 0 開始處理版本，不忽略 0，start 在觀察一位數時為 0~9 的 0，之后才符合我們的遞推公式，那么 count 也是在為一位數時為 10，之后符合遞推公式，這樣之后就不用 n-1，直接用 n 即可

•   public int findNthDigit(int n) {long start = 0;int digit = 1;long count = 10;while(n > count){n -= count;if(start==0)start=10;else start*=10;digit++;count = start * digit * 9;}long num = start + n/digit;return Long.toString(num).charAt(n%digit) - '0';}