概述

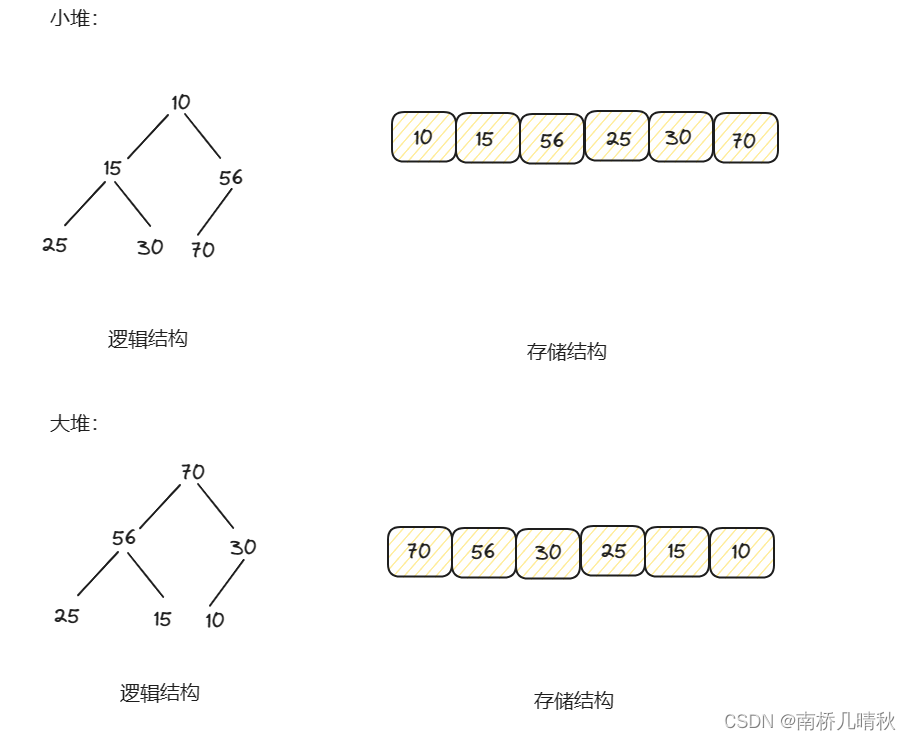
如果有一個關鍵碼的集合K = {k₀,k₁,k₂…k_n-1}，把它的所有元素按完全二叉樹的順序存儲方式存儲在一個一維數組中，并滿足：K_i <=K_2*i+1 且 K_i<=K_2*i+2 (K_i >= K_2*i+1且 K_i>= K_2*i+1) i = 0，1，2…，則稱為小堆(或大堆)。將根節點最大的堆叫做最大堆或大根堆，根節點最小的堆叫做最小堆或小根堆。堆的性質：

• 堆中某個節點的值總是不大于或不小于其父節點的值；
• 堆總是一棵完全二叉樹。

堆的實現

初始化

堆的存儲結構是一個數組，堆的初始化需要定義一個數組，當前元素個數和容量。和順序表的初始化一樣。

typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}

銷毀

釋放數組a的空間，將php->capacity = php->size = 0

void HeapDestroy(HP* php)
{assert(php);free(php->a);php->capacity = php->size = 0;
}

插入

堆的插入是先在數組的最后插入元素，但是需要滿足堆的特點（大堆或小堆），因此需要用到向上調整算法，來實現這一特點。

介紹向上調整算法：

這里小編以實現小堆為例

在數組的最后插入一個元素child，然后這個元素與其雙親節點parent進行比較：

• 如果 child>parent：滿足小堆的條件，無需交換
• 如果 child<parent：不滿足小堆條件，此時需要將孩子節點child與它的雙親結點parent進行交換，此時原來的雙親結點parent變成了孩子結點child，原來的孩子節點child變成了雙親結點parent。此時，再讓現在的雙親結點parent和它的雙親結點parent進行比較，如果不滿足小堆，則繼續交換，繼續比較
• 循環結束的條件是child>0

舉個例子：

如下，在堆中插入元素10：

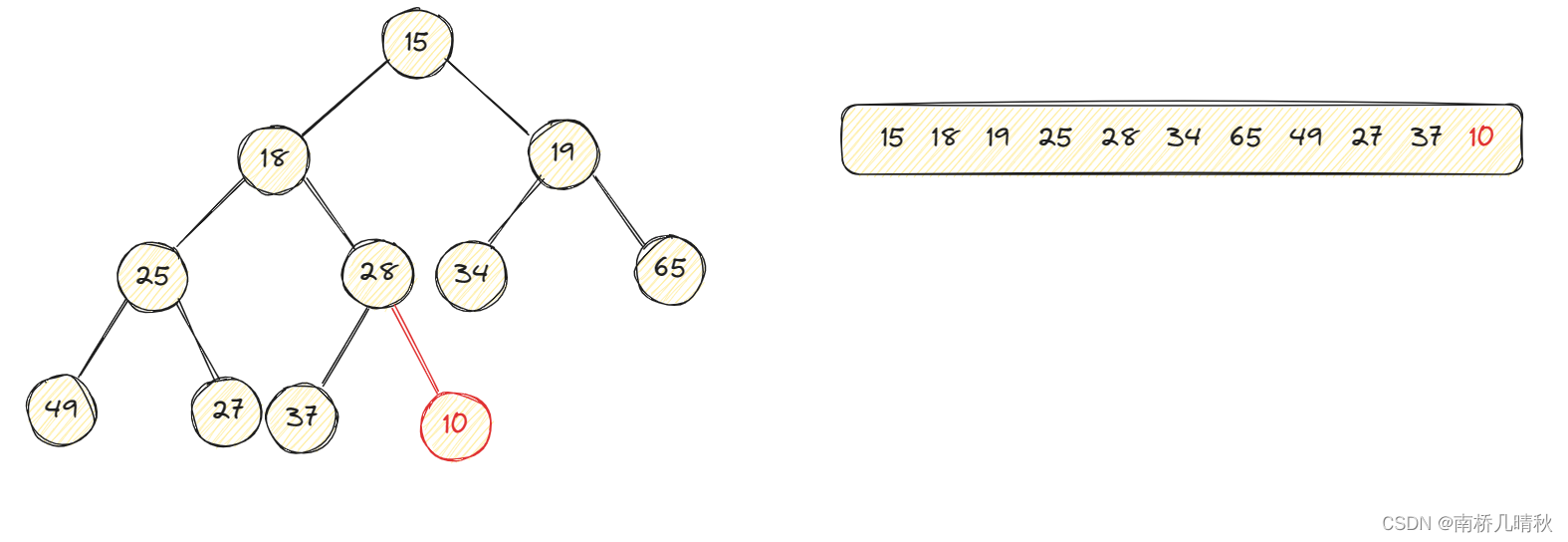
將10與它的雙親結點進行比較，10<28，不滿足小堆的條件，將10和28，進行交換：

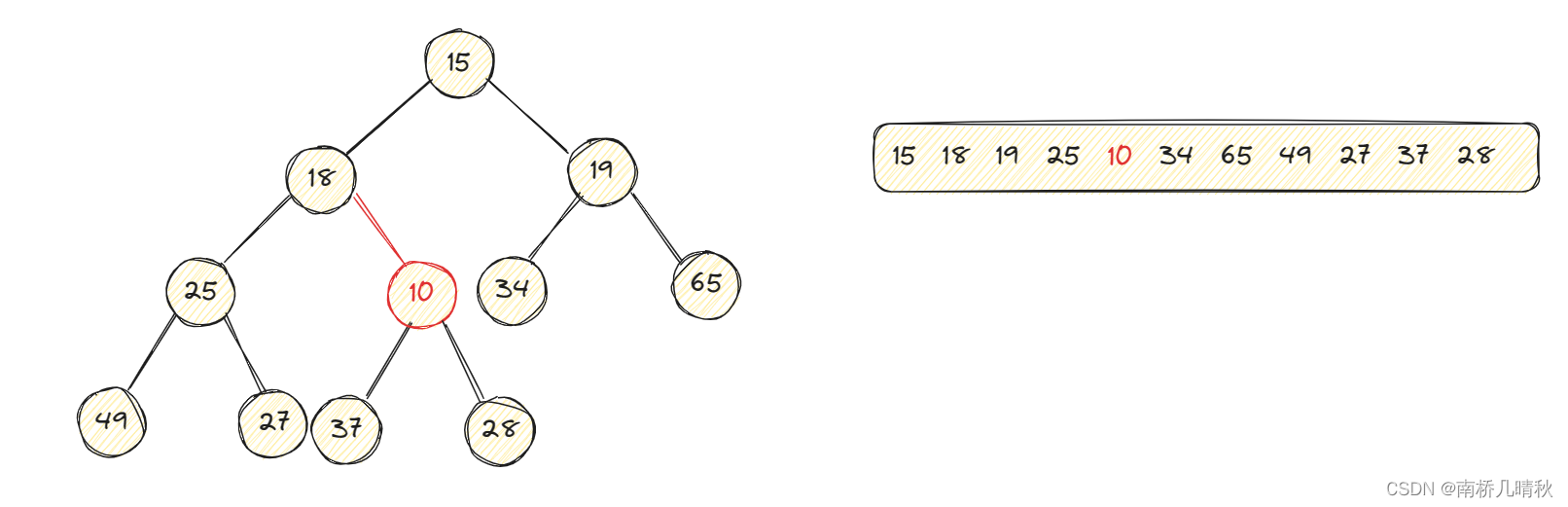
交換完后，此時的10變成了28的雙親結點，28變成了10的孩子結點。現在再將10與它的雙親結點比較，10<18，不滿足小堆的特點，繼續交換。

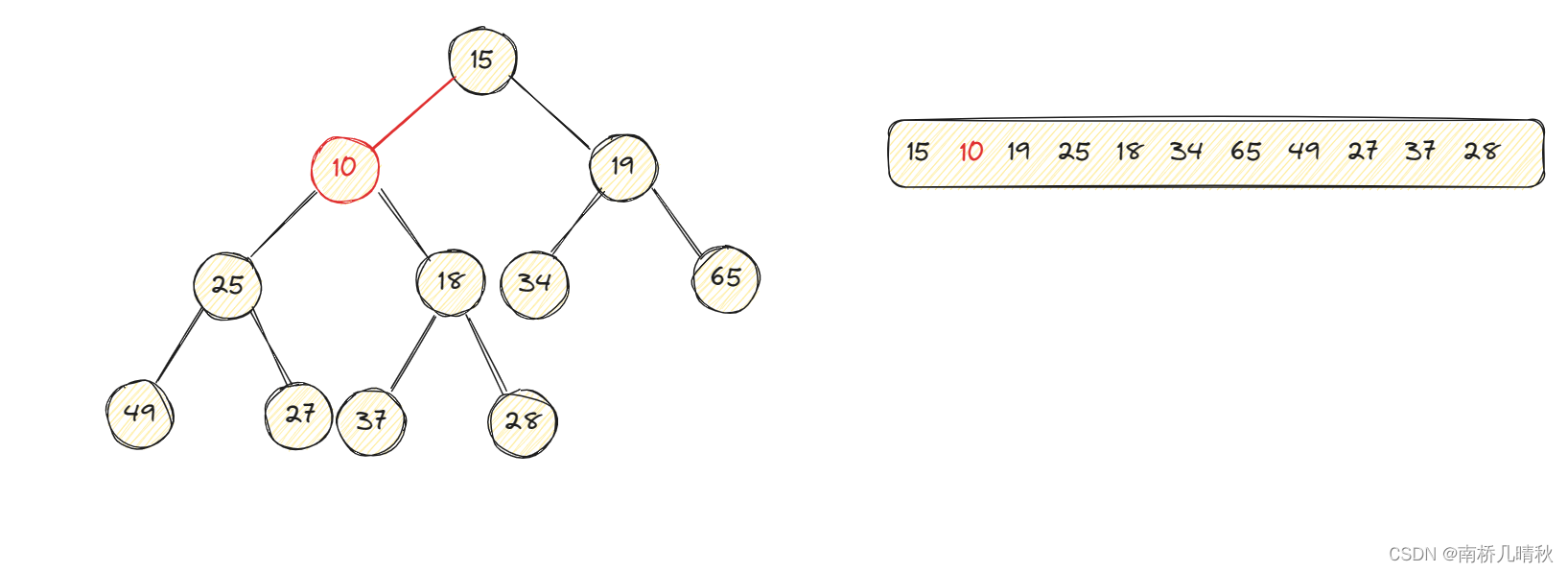
交換完后10變成了18的雙親結點，18變成了10的孩子結點。10和它的雙親結點比較，依然不滿足小堆條件，繼續交換

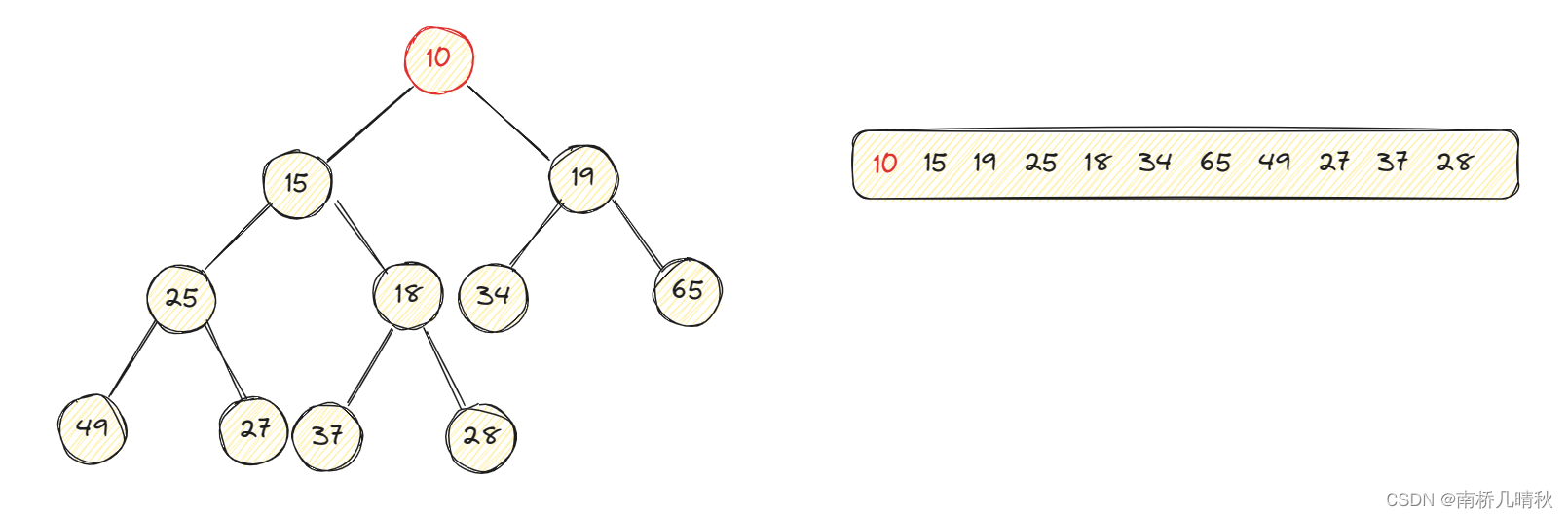
此時，10已經變成了根節點，并且滿足小堆的條件，循環結束。

看了圖解，對向上調整算法有了大概的印象，但是代碼的編寫，還需要再去分析一下。

定義parent是孩子的雙親結點，雙親結點parent與孩子結點child滿足parent = (child - 1) / 2關系。進入循環，比較孩子節點的值和雙親結點的值，判斷是否滿足小堆的條件。

void swap(HPDataType* p1, HPDataType* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

寫完向上調整算法，便可實現插入操作

void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}

刪除

在刪除操作里面，一般規定刪除堆頂，即根節點

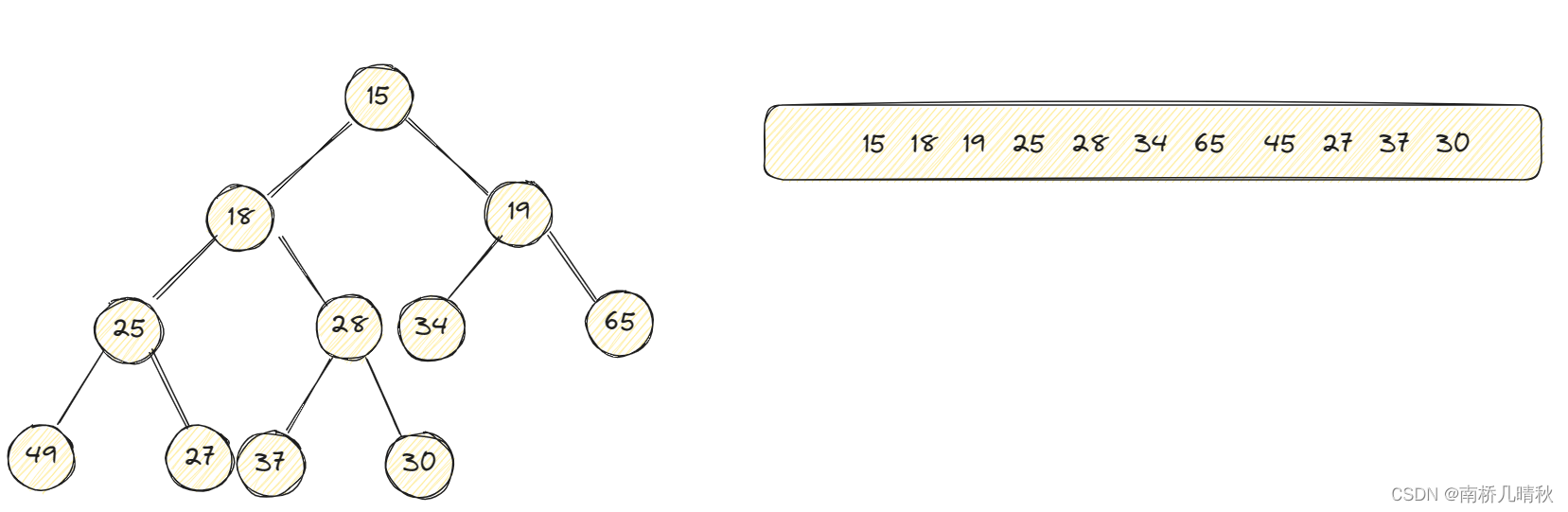
刪除根節點的常規操作是將根結點和最后一個葉節點進行交換，然后尾刪即可，此時根節點的左右子樹依然是小堆

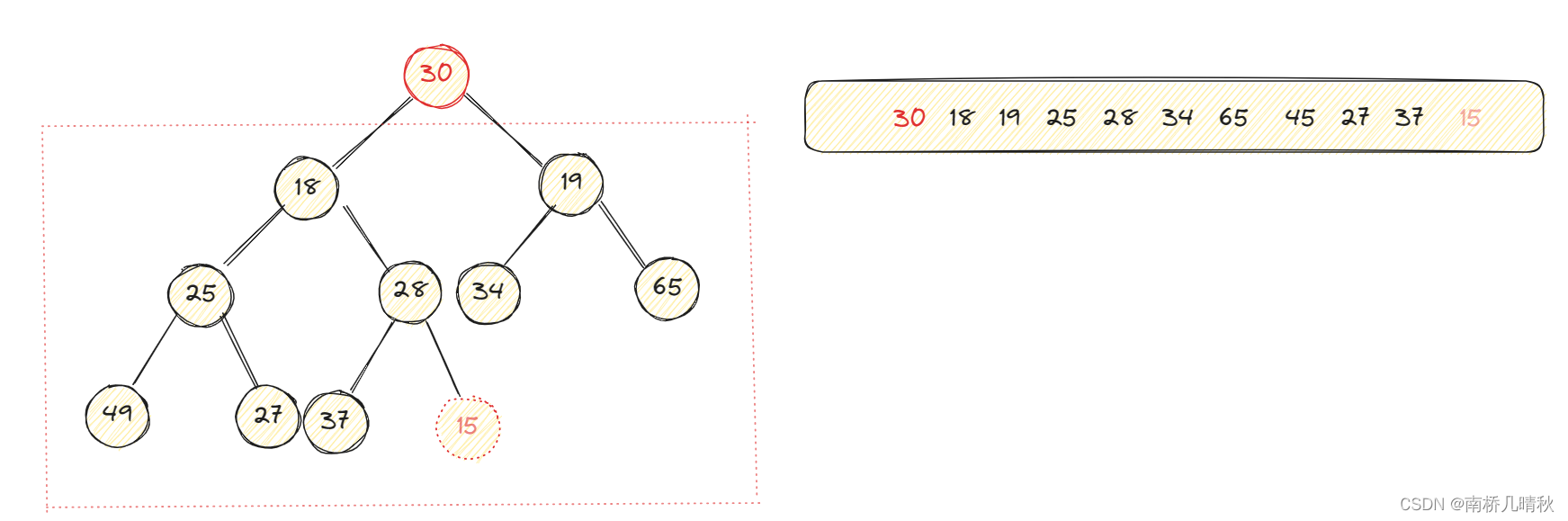
但是根節點不滿足小隊的條件，因此引入向下調整算法

向下調整算法：

和向上調整算法是一個道理

但是此時根節點是雙親結點，有兩個孩子，不知道該選擇哪一個孩子。這里使用到了假設法：假設左孩子小，如果假設錯了，更新一下

判斷雙親結點和孩子結點的大小：

• 如果雙親結點小于孩子結點，直接結束
• 如果雙親結點大于孩子結點，交換雙親結點和孩子結點的值，然后更新一下雙親結點的位置和孩子節點的位置

循環結束的條件是child<size

和向上調整算法基本一致，直接上代碼:

AdjustDown(HPDataType* a,int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (a[child] > a[child + 1] && child + 1 < size){child++;}if (a[child] < a[parent]){swap(a[parent], a[child]);parent = child;child = child * 2 + 1;}else{break;}}
}

刪除操作：

void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}

取堆頂元素

先判斷堆是否存在，然后直接返回堆頂元素即可

HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}

求堆的長度

先判斷堆是否存在，直接返回堆的長度即可

size_t HeapSize(HP* php)
{assert(php);return php->size;
}

判斷堆是否為空

先判斷堆是否存在，如果php->size==0，那么堆為空，返回true，反之返回false

bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}

完整代碼

Heap.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
// 規定刪除堆頂（根節點）
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
size_t HeapSize(HP* php);
bool HeapEmpty(HP* php);

Heap.c

# define _CRT_SECURE_NO_WARNINGS#include"Heap.h"void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}void HeapDestroy(HP* php)
{assert(php);free(php->a);php->capacity = php->size = 0;
}void swap(HPDataType* p1, HPDataType* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}AdjustDown(HPDataType* a,int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (a[child] > a[child + 1] && child + 1 < size){child++;}if (a[child] < a[parent]){swap(a[parent], a[child]);parent = child;child = child * 2 + 1;}else{break;}}
}void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}size_t HeapSize(HP* php)
{assert(php);return php->size;
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}