leedcode 刷題 - 除自身以外數組的乘積

I238. 除自身以外數組的乘積 - 力扣（LeetCode）

給你一個整數數組?nums，返回?數組?answer?，其中?answer[i]?等于?nums?中除?nums[i]?之外其余各元素的乘積?。

題目數據?保證?數組?nums之中任意元素的全部前綴元素和后綴的乘積都在??32 位?整數范圍內。

請?不要使用除法，且在?O(n)?時間復雜度內完成此題。

示例 1:輸入: nums = [1,2,3,4]
輸出: [24,12,8,6]
示例 2:輸入: nums = [-1,1,0,-3,3]
輸出: [0,0,9,0,0]提示：2 <= nums.length <= 105
-30 <= nums[i] <= 30
保證 數組 nums之中任意元素的全部前綴元素和后綴的乘積都在  32 位 整數范圍內進階：你可以在 O(1) 的額外空間復雜度內完成這個題目嗎？（ 出于對空間復雜度分析的目的，輸出數組 不被視為 額外空間。）

題目已經給的很明顯了，就是使用前綴積和后綴積的方式來求解，這種方式其實是一個簡化的動態規劃。

用兩個數組，分別存儲從起始位置到 i 位置的乘積和從末尾位置到 i 位置的乘積；

上述兩個結果對應的就是 f[i]? 和? g[i] 。

遞推公式：

f[i] = f[i - 1] * nums[i - 1];g[i] = g[i + 1] * nums[i + 1];

f[0] 和 g[nums.size()] 都是需要自己手動算的，上述遞推公式是算不出來的。

如果我們像計算題目描述的某個位置（比如是 i 位置）的前綴積和后綴積的話，只需要計算? ? ? ? f[i] * g[i] 既可，因為?f[i] 表示的就是 i 之前的所有積，g[i] 表示的就是 i 之后的所有的積。

完整代碼：

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {vector<int> f(nums.size(), 1);vector<int> g(nums.size(), 1);vector<int> ret(nums.size());for(int i = 1;i < nums.size(); i++) f[i] = f[i - 1] * nums[i - 1];for(int i = nums.size() - 2; i >= 0; i--) g[i] = g[i + 1] * nums[i + 1];for(int i = 0;i < nums.size();i++) ret[i] = g[i] * f[i];return ret;
}
};

I560. 和為 K 的子數組 - 力扣（LeetCode）

給你一個整數數組?nums?和一個整數?k?，請你統計并返回?該數組中和為?k?的子數組的個數?。

子數組是數組中元素的連續非空序列。

示例 1：輸入：nums = [1,1,1], k = 2
輸出：2
示例 2：輸入：nums = [1,2,3], k = 3
輸出：2

?還是使用前綴和，我們可以使用找到一個前綴和 sum[i] 就表示，從數組 0 號位置開始，到 i 位置的所有元素之和。

那么，我們只需要在這個區間當中找到在 [0,i] 這個區間當中,某一個位置作為起始位置（假設為 j? ?），到 i 位置，這個子數組的元素之和等于k，那么，[0,j] 這個區間當中各個元素之和就是? ? ? ? ? ?sum[i] - k;

?往后，只需要? i 往后尋找，就不會找漏。

但是，上述還是有一個問題，如果我們直接遍歷 sum 數組的，來找到 j 這個位置的話，在加上創建 sum 數組的時間復雜度，實際上，這個算法的整個時間復雜度其實還不如暴力解法。

所以，其實我們不用? 循環一個一個去找? j? 位置，我們可以利用一個 hash 表來代替 sum 存儲的這些前綴和的值，也就是代替 sum 存儲其中的每一個元素。

哈希表：? hash<前綴和值，前綴和出現次數>

這樣，如果我們想在? [0,i] 這個區間當中, 找到 j 這個位置，只需要利用 hash 表的快速查找來查找在當前hash 表當中有沒有 sum[i] - k 這個前綴和，同時，利用 hash 表當中的 count（）函數，可以快速查找，這個?sum[i] - k ?出現次數。

關于前綴和加入hash 表的時機：
因為我們的前綴和算法，是要找的是?在 [0,i] 這個區間當中，有多少個前綴和等于sum[i] - k;? ?。

如果直接在一開始就把 sum 計算出來，然后把區間當中前綴和和前綴和出現的次數加入到 hash 表當中是會計算到 i 后面的值。所以不行。

所以，我們在計算 i 位置之前，哈希表里面值存儲 [0, i - 1] 位置的前綴和。

還有一種情況，當當前的整個的前綴和等于 k 的話，那么，在上述的算法當中，其實我們是找不到這個情況的，因為我們找到的是等于 k 的子區間，這個子區間的起始位置上述說過了，是 j ，那么滿足? ?sum[i] - k;?的區間就是 [0, j - 1]，那么在這個情況當中就是 [0, -1] 這個區間，這個區間是不存在的。

所以，我們開始就要默認數組當中有一個和為 0 的前綴和，即： hash[0] = 1;

完整代碼：

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash(nums.size());hash[0] = 1;int sum = 0, ret = 0; // sum 代替sum數組，利用變量給 hash 當中賦值；ret 返回個數for(auto& e : nums){sum += e; // 計算當前的前綴和// 計算滿足 條件的區間，是否在 hash 當中出現。count（）函數判斷是否出現//  出現計數器 加上 這個前綴和 在 hash 當中出現的次數if(hash.count(sum - k)) ret += hash[sum - k]; hash[sum]++;                  }return ret;}
};

I974. 和可被 K 整除的子數組 - 力扣（LeetCode）

給定一個整數數組?nums?和一個整數?k?，返回其中元素之和可被?k?整除的（連續、非空）?子數組?的數目。

子數組?是數組的?連續?部分。

示例 1：輸入：nums = [4,5,0,-2,-3,1], k = 5
輸出：7
解釋：
有 7 個子數組滿足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:輸入: nums = [5], k = 9
輸出: 0

要解決這道題目，首先要知道同于定理?

也就是 如果 a 和 b 的差值，除上 p ，如果是整除的話，也就是余數是零的話，a 除上 p 的余數 =? ? b 除上 p 的余數。

而且，還需要清楚，在C++ 當中， [負數 % 正數] 的結果是一個負數。

?也就是說，其實[負數 % 正數] ? 其實結果也是一個余數，但是這個余數是負數。

所以，針對這種情況，我們要對這個負數進行修正，把他修正為正數。

所以，當我們在計算?[負數 % 正數] 的結果之時，其實，計算出的負數的結果在加上模數（也就是其中的正數），其實就是對應的正數的結果。如下圖所示：
?

上述的計算方式對于 a 是負數的情況來說，計算出的結果就是修正之后的結果，也就是修正為正數之后的結果。

但是上述的修正方式對于 a 是正數的情況是計算錯誤的，因為對于 a 是正數的情況來說， a % b 本來就是正確的結果，但是后面又加上了一個 b，所以是不正確的。

所以，為了正數和負數統一，我們共用的方式就是? 在上述計算式子當中，再 % b 即可。

上述式子就是我們想要的i修正公式了。

所以，按照和這個問題其實就和上述和為K的子數組求解方式一樣了。

先求出所有的從 0 號數組位置開始的所以前綴模，保存到一個數組當中，然后求出與 K 模的余數即可。

同樣優化方式和上述一樣，不需要多定義一個數組來保存前綴模，這樣也不好查找對應的前綴模，只需要用一個 hash表來存儲即可。

上述問題就被簡化為了在 [0, i - 1] 這個區間當中，找到有多少個前綴和的余數等于 (sum %? k + k ) % k。

完整代碼：
?

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0 % k] = 1; // 0 這數的余數int sum = 0, ret = 0;for(auto& e : nums){sum += e;int r = (sum%k + k) % k;if(hash.count(r)) ret += hash[r];hash[r]++;}return ret;}
};

I525. 連續數組 - 力扣（LeetCode）

?給定一個二進制數組?nums?, 找到含有相同數量的?0?和?1?的最長連續子數組，并返回該子數組的長度。

示例 1:輸入: nums = [0,1]
輸出: 2
說明: [0, 1] 是具有相同數量 0 和 1 的最長連續子數組。
示例 2:輸入: nums = [0,1,0]
輸出: 2
說明: [0, 1] (或 [1, 0]) 是具有相同數量0和1的最長連續子數組。

在數組當中，所有的元素的值要么是 0 ，要么是1。我們需要找到一個符合要求的最長的連續的子數組，返回這個子數組的長度。

我們在統計個數的時候，其實是可以做到轉化的，如果把 0 全部替換為-1，那么我們統計個數的問題，其實就轉化成了找到一個元素之和等于 0 的子數組。

所以，這道題目就可以使用前綴和的方法來解決。

使用hash 表來存儲前綴和為 sum 的區間，所以嗎，應該是 unordered_map<sum, i > （其中 sum 是前綴和，i 是這個前綴和區間的下標）。

當找到某一個下標，和為? sum，計算出這個區間的長度，就把這個對應的綁定的值存入到哈希表當中。

如果有重復的 sum，但是區間不一樣，不需要重新更新原本在 hash 表當中的 <sum , i>，只需要保留之前存入的 <sum, i> 即可。因為，我們需要找到子區間最長的子數組，那么下標應該是越考左，那么計算出的子區間長度才是最大的。

同樣，為了處理特殊情況：當 [0?, i] 這個子區間計算出的前綴和就是0了，那么按照上述? 和為K的子數組這個題目當中邏輯去找到子區間的話，就會在 -1 為開始的區間去找。

所以，我們需要在開始默認一個子區間的前綴和是0，即? hash[0] = -1;

上述的過程就可以找出所有的合法的子數組了，現在就是如何計算這個子數組的區間大小？

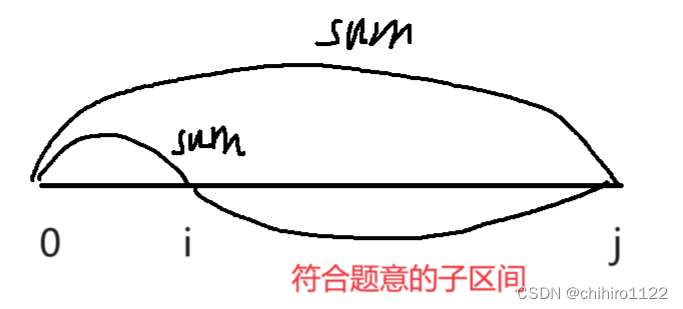
如上，我們只需要找出 i 和 j 兩個下標，使得 [0, i] 的前綴和和 [0, j] 的前綴和相等即可。

?所以我們計算出的區間的長度就是 i - j 。

完整代碼：

class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int ,int> hash;hash[0] = -1;   // 默認 剛開始 哈希表當中有一個 前綴和為0 的區間int sum = 0, ret = 0;for(int i = 0 ;i < nums.size(); i++){sum += nums[i] == 0 ? -1 : 1; // 如果是 0 就加-1，如是1 就加 1// 如果 sum 在hash 當中存在，說明此時就已經找到了 符合條件的子區間// 那么就更新的 ret 返回值。if(hash.count(sum)) ret = max(ret, i - hash[sum] + 1 - 1);else hash[sum] = i;  // sum 在 hash 當中不存在，那么 就添加一個 hash 元素}return ret;}
};