合并區間-力扣算法題56題
以數組?intervals?表示若干個區間的集合,其中單個區間為?intervals[i] = [starti, endi]?。請你合并所有重疊的區間,并返回?一個不重疊的區間數組,該數組需恰好覆蓋輸入中的所有區間?。
示例 1:
輸入:intervals = [[1,3],[2,6],[8,10],[15,18]] 輸出:[[1,6],[8,10],[15,18]] 解釋:區間 [1,3] 和 [2,6] 重疊, 將它們合并為 [1,6].
示例?2:
輸入:intervals = [[1,4],[4,5]] 輸出:[[1,5]] 解釋:區間 [1,4] 和 [4,5] 可被視為重疊區間。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
java實現算法代碼
class Solution {public int[][] merge(int[][] intervals) {if (intervals.length == 0) {return new int[0][2];}Arrays.sort(intervals, new Comparator<int[]>() {public int compare(int[] interval1, int[] interval2) {return interval1[0] - interval2[0];}});List<int[]> merged = new ArrayList<int[]>();for (int i = 0; i < intervals.length; ++i) {int L = intervals[i][0], R = intervals[i][1];if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {merged.add(new int[]{L, R});} else {merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);}}return merged.toArray(new int[merged.size()][]);}
}
算法思路(力扣的思路)
如果我們按照區間的左端點排序,那么在排完序的列表中,可以合并的區間一定是連續的。如下圖所示,標記為藍色、黃色和綠色的區間分別可以合并成一個大區間,它們在排完序的列表中是連續的:?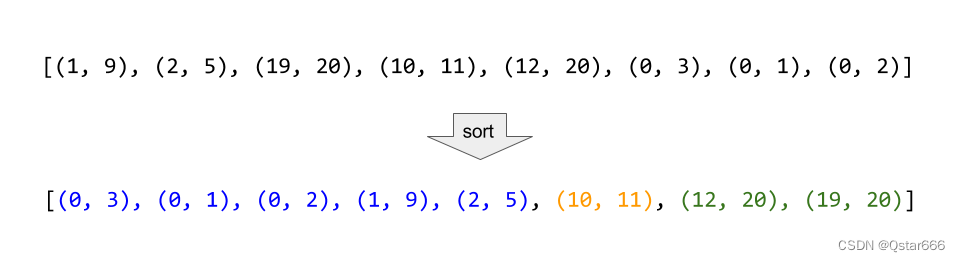
?
算法
我們用數組 merged 存儲最終的答案。
首先,我們將列表中的區間按照左端點升序排序。然后我們將第一個區間加入 merged 數組中,并按順序依次考慮之后的每個區間:
如果當前區間的左端點在數組 merged 中最后一個區間的右端點之后,那么它們不會重合,我們可以直接將這個區間加入數組 merged 的末尾;
否則,它們重合,我們需要用當前區間的右端點更新數組 merged 中最后一個區間的右端點,將其置為二者的較大值。
正確性證明
上述算法的正確性可以用反證法來證明:在排完序后的數組中,兩個本應合并的區間沒能被合并,那么說明存在這樣的三元組 (i,j,k) 以及數組中的三個區間 a[i],a[j],a[k]?滿足 i<j<k?并且 (a[i],a[k])可以合并,但 (a[i],a[j])?和 (a[j],a[k]) 不能合并。這說明它們滿足下面的不等式:
a[i].end<a[j].start(a[i]?和?a[j]?不能合并)a[j].end<a[k].start(a[j]?和?a[k]?不能合并)a[i].end≥a[k].start(a[i]?和?a[k]?可以合并)
????????????????????????a[i].end<a[j].start(a[i]?和?a[j]?不能合并)
????????????????????????a[j].end<a[k].start(a[j]?和?a[k]?不能合并)
????????????????????????a[i].end≥a[k].start(a[i]?和?a[k]?可以合并)
我們聯立這些不等式,可以得到:
????????????????????????????????????????a[i].end<a[j].start≤a[j].end<a[k].start
產生了矛盾!這說明假設是不成立的。因此,所有能夠合并的區間都必然是連續的。
我的思路
1.先判斷該?intervals是否為空,為空則返回一個空的二維數組int[0][2]
2.不為空的話,先用Array.sort(T[] a,Comparator<? super T> c)來定制一個只比較數組的最左端并使用升序排序的Compare排序器
3.之后將二維數組封裝在一個List集合里面,進行下一步比較
4.有兩種情況
????????4.1. 如果第一個區間的最右端的值小于下一個區間的最左端的值,則在List集合中再添加一個區間
? ? ? ? 4.2. 如果第一個區間的最右端的值大于等于下一個區間最左端的值,則將第一個區間最右端的值修改為下一個區間最右端的值
5.將List轉換為數組并以二維數組的形式返回即可
使用方法Arrays.sort和Comprator
Arrays.sort使用文檔
- public static?<T>?void?sort?(T[]?a, Comparator<? super T>?c)
- 根據指定比較器引發的順序對指定的對象數組進行排序。 數組中的所有元素都必須是指定比較相互比較的 (即,
c.compare(e1, e2)不得拋出ClassCastException任何元件e1和e2陣列中)。這種保證是穩定的 :相同的元素不會因排序而重新排序。
實現注意事項:此實現是一個穩定的,自適應的迭代合并輸出,當輸入數組部分排序時,需要遠遠少于n lg(n)的比較,同時在輸入數組隨機排序時提供傳統mergesort的性能。 如果輸入數組幾乎排序,則實現需要大約n次比較。 臨時存儲要求從幾乎排序的輸入數組的小常量到隨機排序的輸入數組的n / 2個對象引用不等。
該實現在其輸入數組中具有升序和降序的相同優勢,并且可以利用同一輸入數組的不同部分中的升序和降序。 它非常適合合并兩個或多個排序數組:只需連接數組并對結果數組進行排序。
參數類型
T- 要排序的對象的類參數
a- 要排序的數組
c- 用于確定陣列順序的比較器。null值表示應使用元素' natural ordering 。異常
ClassCastException- 如果數組包含使用指定比較器無法 相互比較的元素
IllegalArgumentException- (可選)如果發現比較器違反了Comparator合同
?Comprator使用文檔
Collections.sort或Arrays.sort),以便精確控制排序順序。 比較器還可用于控制某些數據結構的順序(例如sorted sets或sorted maps),或者為沒有natural ordering的對象集合提供排序。比較器
c對一組元素S施加的排序被認為與等號一致,當且僅當c.compare(e1, e2)==0具有與e1.equals(e2)(e1和e2在S中的S相同的布爾值時。當使用能夠強加與equals不一致的排序的比較器來排序有序集(或有序映射)時,應該謹慎行事。 假設具有顯式比較器
c的有序集(或有序映射)與從集合S提取的元素(或鍵)S。 如果c對S的排序與equals不一致,則排序集(或有序映射)將表現得“奇怪”。 特別是有序集(或有序映射)將違反集合(或映射)的一般合同,其定義為equals。例如,假設有兩個元素
a和b,使(a.equals(b) && c.compare(a, b) != 0)為空TreeSet,比較器為c。 第二個add操作將返回true(并且樹集的大小將增加)因為a和b在樹集的視角中不相等,即使這與Set.add方法的規范相反。注意:這通常是一個好主意比較,也能實現
java.io.Serializable,因為它們可能被用來作為排序的序列化數據結構的方法(如TreeSet,TreeMap)。 為了使數據結構成功序列化,比較器(如果提供)必須實現Serializable。對于數學上的傾斜,即限定了施加順序給定的比較器的關系
c上一組給定對象強加S是:{(x, y) such that c.compare(x, y) <= 0}.此總訂單的商是:{(x, y) such that c.compare(x, y) == 0}.它從合同緊跟compare,該商數是一個等價關系S,并且實行排序是全序S。 當我們說c對S施加的排序與equals一致時 ,我們的意思是排序的商是由對象'equals(Object)方法定義的等價關系:{(x, y) such that x.equals(y)}.與
Comparable不同,比較器可以選擇允許比較空參數,同時保持對等關系的要求。
聲明
部分算法思路摘自力扣(位置在算法思路這個目錄里),其余均為個人創作
作者:力扣官方題解
鏈接:https://leetcode.cn/problems/merge-intervals/
來源:力扣(LeetCode)






)



----鏈表--兩數相加)
)

)

:012茶、花椒、八角、肉桂、杜仲、厚樸、枸杞、忍冬)



