問題描述

假設有一個貨郎擔要拜訪n個城市，他必須選擇所要走的路程，路程的限制時每個城市只能拜訪一次，而且最后要走到原來出發的城市，要求路徑長度。

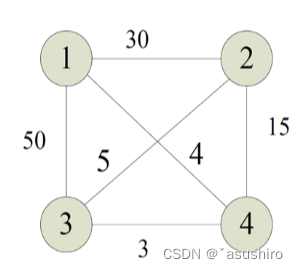
旅行商問題將要走過的城市建立成一個完全圖。稠密圖，所以用臨接矩陣來存。
由于路徑的特殊性，可以正走也可以反著走，所以一般存在兩條最優路徑同時也可以用這條性質檢驗算法的正確性。

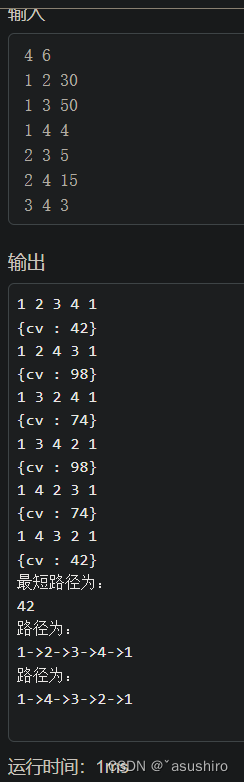
暴力枚舉

使用dfs枚舉每一個點， 不適用剪枝的話就是暴力枚舉方法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;const int N = 10;int g[N][N], n, m;
int cv = 0, bv = 0x3f3f3f3f;
bool st[N];vector<int> ans, x;void dfs(int k)
{if (k == n){// printf("before cv : %d\n", cv);// printf("last : {%d, %d} = %d\n", 1, x[k - 1], g[1][x[k - 1]]);cv += g[1][x[k - 1]];x.push_back(x[0]);for (auto i : x)printf("%d ", i);puts("");printf("{cv : %d}\n", cv);if(cv < bv){bv = cv;ans = x;}cv -= g[1][x[k - 1]];//注意最后一個加的cv要減掉x.pop_back();//同樣也要刪掉return;}for (int i = 1; i <= n; i ++){if (!st[i]){st[i] = true;x.push_back(i);//注意x的添加要在前面不然后面下標會出錯cv += g[x[k - 1]][i];// printf("{%d, %d} : %d\n", x[k - 1], i,  g[x[k - 1]][i]);dfs(k + 1);cv -= g[x[k - 1]][i];x.pop_back();st[i] = false;}}
}void out()
{puts("路徑為：");for (int i = 0; i <= n; i ++){printf("%d", ans[i]);printf(i == n ? "\n" : "->");}
}int main()
{memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}for (int i = 0; i <= n; i ++) g[i][i] = 0; st[1] = true; x.push_back(1);dfs (1);puts("最短路徑為：");printf("%d\n", bv);out();reverse(ans.begin(), ans.end());out();puts("");return 0;
}

回溯法

回溯法就是在暴力枚舉的是后加上剪枝函數減少枚舉的結點數目
剪枝函數為
左剪枝：
$$當cv>bv時減去$$

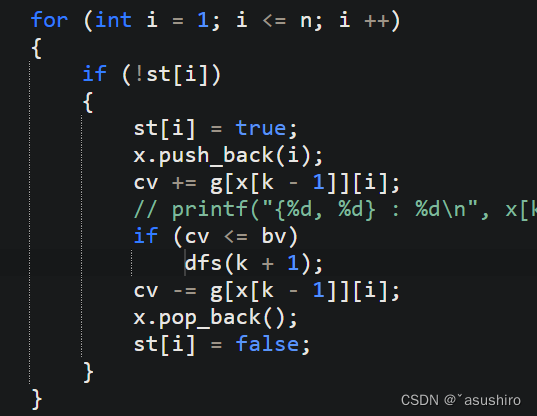
在暴力枚舉的基礎上加上這個剪枝函數就行

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;const int N = 10;int g[N][N], n, m;
int cv = 0, bv = 0x3f3f3f3f;
bool st[N];vector<int> ans, x;void dfs(int k)
{if (k == n){// printf("before cv : %d\n", cv);// printf("last : {%d, %d} = %d\n", 1, x[k - 1], g[1][x[k - 1]]);cv += g[1][x[k - 1]];x.push_back(x[0]);for (auto i : x)printf("%d ", i);puts("");printf("{cv : %d}\n", cv);if(cv < bv){bv = cv;ans = x;}cv -= g[1][x[k - 1]];//注意最后一個加的cv要減掉x.pop_back();//同樣也要刪掉return;}for (int i = 1; i <= n; i ++){if (!st[i]){st[i] = true;x.push_back(i);cv += g[x[k - 1]][i];// printf("{%d, %d} : %d\n", x[k - 1], i,  g[x[k - 1]][i]);if (cv <= bv)dfs(k + 1);cv -= g[x[k - 1]][i];x.pop_back();st[i] = false;}}
}void out()
{puts("路徑為：");for (int i = 0; i <= n; i ++){printf("%d", ans[i]);printf(i == n ? "\n" : "->");}
}int main()
{memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}for (int i = 0; i <= n; i ++) g[i][i] = 0; st[1] = true; x.push_back(1);dfs (1);puts("最短路徑為：");printf("%d\n", bv);out();reverse(ans.begin(), ans.end());out();puts("");return 0;
}

搜索的結點數變成了

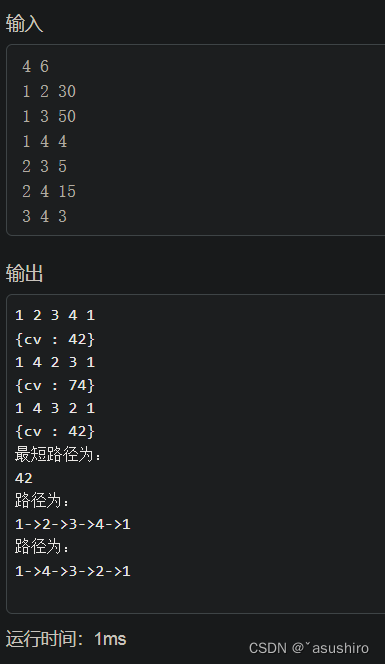
相比窮舉減少了搜索的結點數

動態規劃法

狀態壓縮dp
利用一個int位中的32位0/1bit碼來表示圖走了哪些點，如果此位為1表示經過，0表示還未經過

類似題目AcWing 91. 最短Hamilton路徑

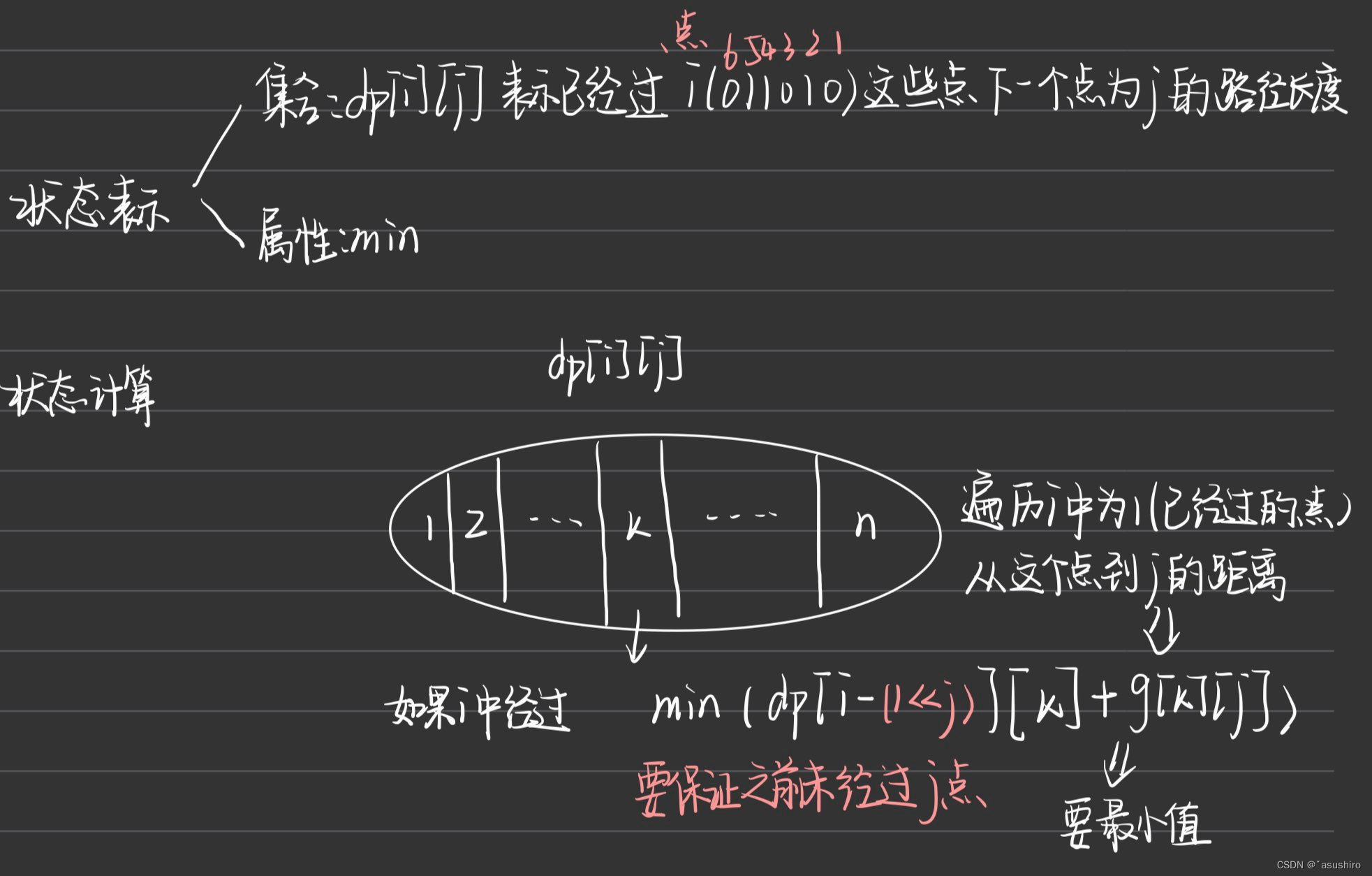
/*由于要遍歷每一個點所以不能用最短路徑算法從一個已知點到另一個點只需要關注兩個狀態：1、終點是什么， 2、經過了哪些點而dp[i][j] 表示從0到終點j，經過了二進制狀態（每個點有走過和沒走兩個狀態）的點的路徑狀態計算：dp[i][j] <- dp[i - j][k](在已經經過的點中，去掉點j的方案取最小)
*/
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 21, M = 1 << N;
int dp[M][N];
int w[N][N];
int n;int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++)for (int j = 0; j < n; j ++)scanf("%d", &w[i][j]);memset(dp, 0x3f, sizeof dp);dp[1][0] = 0;for (int i = 0; i < 1 << n; i ++)for (int j = 0; j < n; j ++)if (i >> j & 1)for (int k = 0; k < n; k ++ )if (i >> k & 1)dp[i][j] = min(dp[i][j], dp[i - (1 << j)][k] + w[j][k]);// 轉移到達第i個點時將第i個點的狀態要去掉就// 例如要將100101的第2個點去掉就需要 - 000100 = 100001printf("%d\n", dp[(1 << n) - 1][n - 1]);// 100000 - 000001 = 0111111 要將n - 1位全置位為1只需要用n為1后面為0減個位1即可return 0;
}

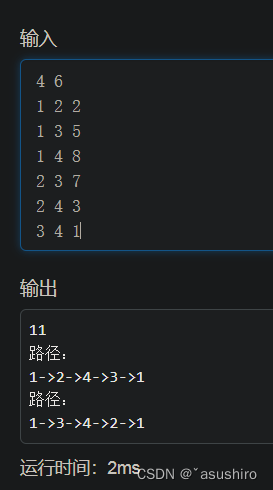
貪心法

貪心就是從起點開始每次走從這個點出發權重最小的邊
但是這個尋找局部最優解的過程找到的并不是全局最優解
思路和生成最小生成樹的思路一樣，由于是完全圖稠密圖，所以使用prim算法更好

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 510, INF = 0x3f3f3f3f;int g[N][N], dist[N];
bool st[N];
int n, m;
vector<int> ans;int prime()
{memset(dist, 0x3f, sizeof dist);int res = 0;// 最小生成樹中的權重之和for (int i = 0; i < n; i ++){int t = -1;// t表示集合外與集合相連的邊最小的結點for (int j = 1; j <= n; j ++)if (!st[j] && (t == -1 || dist[j] < dist[t]))// 集合外的，第一次直接賦值，值更小的t = j;st[t] = true;// 加入集合ans.push_back(t);if (i && dist[t] == INF) return INF;// 不是第一個節點且到集合的距離無窮，說明各個結點都不連通if (i) res += dist[t];for (int j = 1; j <= n; j ++)dist[j] = min (dist[j], g[t][j]);// 更新與集合相連的最小值}return res;
}void out()
{puts("路徑：");for (int i = 0; i <= n; i ++){printf("%d", ans[i]);printf(i == n ? "\n" : "->");}
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g);for (int i = 0; i < m; i ++){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min (g[a][b], c);// 無向圖要將兩個方向的邊都賦上權重}int res = prime();if (res == INF) puts("impossible");else printf("%d\n", res + g[ans[n - 1]][1]);ans.push_back(ans[0]);out();reverse(ans.begin(), ans.end());out();return 0;
}

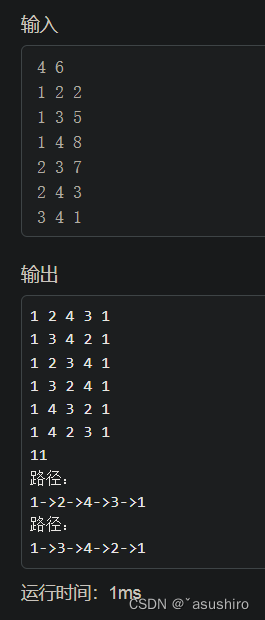
分支界限法

使用優先隊列形式
cc為當前代價，rc為剩余結點的最小出邊代價和
下界函數為: cc + rc
左剪枝：
$$當cc>bc時剪枝$$
右剪枝：
$$當cc+rc>bc是剪枝$$

歸結左右剪枝都可以用bound = cc + rc進行剪枝

剩余結點最小出邊代價和就是枚舉剩余每條結點對沒給結點只算最小的出邊

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>using namespace std;const int N = 16;
const int INF = 0x3f3f3f3f;int g[N][N], n, m, bc = INF;
vector<int> ans;struct Node {int idx, cost, bound;vector<int> path;bool st[N];bool operator<(const Node& other) const {return bound + cost > other.bound + other.cost;  // 按照 bound + cost 降序排序}
};int bound(const Node& x) {int minCost = 0;for (int i = 1; i <= n; ++i) {if (x.st[i]) {int m = INF;for (int j = 1; j <= n; ++j) {if (x.st[j]) {m = min(m, g[i][j]);}}minCost += m;}}return minCost;
}void bfs() {priority_queue<Node> heap;Node head = {1, 0, 0, {1}, {false}};head.st[1] = true;heap.push(head);while (heap.size()) {auto t = heap.top();heap.pop();if (t.idx == n) {int cc = t.cost + g[t.path[t.idx - 1]][1];for (auto i : t.path)printf("%d ", i);printf("%d", 1);puts("");if (cc < bc){bc = cc;ans = t.path;}continue;}for (int i = 1; i <= n; ++i) {if (!t.st[i]) {Node newNode = t;newNode.st[i] = true;newNode.path.push_back(i);newNode.cost += g[newNode.path[newNode.idx - 1]][i];newNode.idx++;newNode.bound = bound(newNode); if(newNode.bound < bc)//左右剪枝通用，因為是排列樹左右都要算下界函數heap.push(newNode);}}}
}void out()
{puts("路徑：");for (int i = 0; i <= n; i ++){printf("%d", ans[i]);printf(i == n ? "\n" : "->");}
}int main() {memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);for (int i = 0; i < m; ++i) {int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}bfs();printf("%d\n", bc);ans.push_back(ans[0]);out();reverse(ans.begin(), ans.end());out();return 0;
}