一、MATLAB中傳遞函數的表示

在繪制系統的根軌跡之前，需要知道傳遞函數在matlab中如何表示。
在matlab中，通常用向量表示一個多項式。例如P=[1 2 3 ]表示 F(s)=s²+2s+3。而對于傳遞函數的表示，通常利用一個向量num表示其分子多項式，den表示分母多項式。例如表示$F(s)=\frac{3s^2+s}{s^3+5s+8}$的代碼如下：

clear all;
close all;
num=[3 1 0];
den=[1 0 5 8];
sys=tf(num,den)

運行結果：

sys =3 s^2 + s-------------s^3 + 5 s + 8Continuous-time transfer function.

如果是兩個多項式是相乘的形式，可以利用conv()函數。例如Fs=(s²+3s+1)(4s+1),則可以用den=conv([1 3 1],[4 1])計算出兩個多項式相乘后的系數。

二、rlocus函數繪制根軌跡

MATLAB提供rlocus函數可以直接用于繪制系統的根軌跡。還能夠允許用戶交互式的選取根軌跡上的值。下表是rlocus函數的常見用法。

函數	使用說明
rlocus(G)	繪制開環傳遞函數為G的根軌跡
rlocus(G1,G2,…)	在同一張圖上繪制多個系統的根軌跡
rlocus(G,k)	繪制系統的給定增益向量k的根軌跡
[r,k]=rlocus(G)	返回根軌跡參數，r為閉環特征根
r=rlocus(G,k)	返回系統的開環增益為k時的閉環特征根

下面分別演示常規根軌跡、參數根軌跡和零度根軌跡的繪制步驟。

1.常規根軌跡仿真示例

例： 某系統的結構如下圖所示，繪制出其根軌跡。

其中:$$G(s)H(s)=\frac{K^{?}(s+5)}{(s+2)(s+3)}.$$
求解程序如下：

clear all;
close all;
num=[1 5];%num表示傳遞函數分子多項式系數向量
den=conv([1 2],[1 3]);%den表示傳遞函數分母多項式系數向量
sys=tf(num,den);%得到傳遞函數sys
rlocus(sys)%繪制根軌跡，也可以用rlocus(num,den)直接繪制。

運行結果如下圖：

2.參數根軌跡仿真示例

繪制參數根軌跡和繪制常規根軌跡的過程基本上相同。只需要在繪制參數根軌跡之前，引入“等效開環傳遞函數”，將繪制參數根軌跡的問題化為繪制K^*變化時的根軌跡形式來處理。
例： 單位負反饋系統開環傳遞函數為$$G(s)=\frac{k}{s(s+2k)}.$$
繪制出k=0→∞時的根軌跡。
解： 首先將上述傳遞函數轉化為：
$$G^{?}(s)=\frac{k(2s+1)}{s^2}.$$
然后就按照常規根軌跡的繪制步驟進行繪制，代碼如下：

clear all;
close all;
num=[2 1];
den=[1 0 0];
rlocus(num,den);

運行結果如下：

3.零度根軌跡仿真示例

繪制零度根軌跡和繪制常規根軌跡的過程也基本上相同。唯一的差別是在繪制零度根軌跡時，需要在表示傳遞函數分子多項式的系數前添加一個負號，舉個例子如下。
例： 某正反饋系統的結構圖如下所示，

其中:$$G(s)H(s)=\frac{K^{?}s(s+5)}{(s+8)(s^2+2s+2)}.$$
試繪制出根軌跡。
代碼如下：

clear all;
close all;
num=[-1 -5 0];
den=conv([1 8],[1 2 2]);
Gs=tf(num,den);
rlocus(Gs)

運行結果如下：

三、圖形化工具rltool介紹

MATLAB的rltool工具是一個圖形化的工具，能夠顯示出系統的根軌跡以及系統的響應，同時也能夠繪制系統的Bode圖、奈奎斯特圖和Nichols圖等。rltool工具提供了一個非常直觀的界面，幫助用戶設計、分析和仿真控制系統，使得控制器的設計變得更加簡單和高效。
下圖是rltool工具界面的介紹。

rltool工具默認的系統結構如下圖所示，

其中G為被控對象，也就是輸入rltool(sys)命令時傳遞函數sys，C為控制器（補償器），在本文中C的值就是開環增益K的值。如果要改變系統的結構圖，在菜單欄的第三項“Edit Architecture”中選擇系統結構。
rltool常用命令如下表：

函數	說明
rltool	打開rltool工具
rltool(PLANT)	指定被控對象G的模型，PLANT是用TF、ZPK或SS創建的任何線性模型。
rltool(PLANT,COMP)	進一步指定控制器C的模型，COMP是用TF、ZPK或SS創建的任何線性模型。
rltool(PLANT,COMP,LocationFlag,FeedbackSign)	LocationFlag指定控制器的位置，FeedbackSign決定反饋符號。LocationFlag=‘forward’時，控制器C在前向通道上；LocationFlag=‘feedback’時,控制器C在反饋回路上；FeedbackSign='-1’為負反饋；FeedbackSign=’1‘為正反饋。

---

通過以下的例子來簡單介紹rltool工具的使用方法。

例： 某系統的方框圖下圖所示，

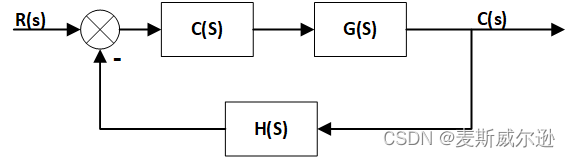
已知該系統為單位負反饋系統，被控對象為$$G(s)=\frac{1}{s^3+20s^2+100s}$$,其中C(s)為比例控制器，$C(s)=K$，試繪制出K=0→∞時的系統根軌跡，另外討論分別加入環節(s+4)和(s+2)對系統根軌跡的影響（C(s)=K(s+4)和C(s)=K(s+2)），并用階躍響應驗證結果。
解：
程序代碼如下：

clear all;
close all;
num=[1];
den=[1 20 100 0];
Gs=tf(num,den);%建立被控對象傳遞函數
rltool(Gs)%打開rltool工具界面

運行以上代碼過后，進入到rltool工具的界面，如下圖所示。其界面會顯示出該系統的根軌跡圖和K=1時系統的階躍響應。根軌跡圖中的紅點表示當前系統的閉環特征根，可以拖動紅點來改變當前系統的閉環特征根，拖動紅點的同時系統的階躍響應也會發生改變。而此時左邊"Controllers or Fixed Blocks"狀態欄中C的值就是當前系統的開環增益。

然后給系統添加一個環節（s+4），只需要在根軌跡圖右擊鼠標，選擇添加零點極點"Add Pole or Zero"即可，如下如圖所示，

選擇"Real Zero"添加實數零點，再在實數坐標上點擊’-4‘的位置，添加完成后如下圖所示，可以看到此時C的值為(s+4)。為了下一步能和添加環節(s+2)后對比系統的階躍響應，先將該系統儲存起來，點擊菜單欄的"Store"選項儲存為Design1。

接下來添加環節(s+2)，只需要將剛才的“-4”零點拖拽到“-2”處，添加過后的結果如下圖所示，

為了對比兩個環節的階躍響應，首先把兩個系統的開環增益都設置為了1(也就是把控制圖中C的值設置為1)然后再點擊"Compare"選項選擇Design1和當前系統進行對比，對比圖如下，

其中，藍色曲線為當前系統的階躍響應(添加了環節(s+2)的系統)，綠色曲線為Design1的系統階躍響應(添加了環節(s+4)的系統)。

rltool的功能遠不止畫根軌跡，它也可以畫Bode圖、奈奎斯特圖等等，能夠對系統時域和頻域分析起到很大的幫助，大家可以根據自己需要自行去探索