文檔講解:代碼隨想錄
視頻講解:代碼隨想錄B站賬號
狀態:看了視頻題解和文章解析后做出來了
300.最長遞增子序列?
class Solution: # 2516 ms, faster than 64.96%def lengthOfLIS(self, nums: List[int]) -> int:n = len(nums)dp = [1] * nfor i in range(1, n):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[j] + 1, dp[i])return max(dp)- 時間復雜度:O(n^2)
- 空間復雜度:O(n)
1. 確定dp數組的含義
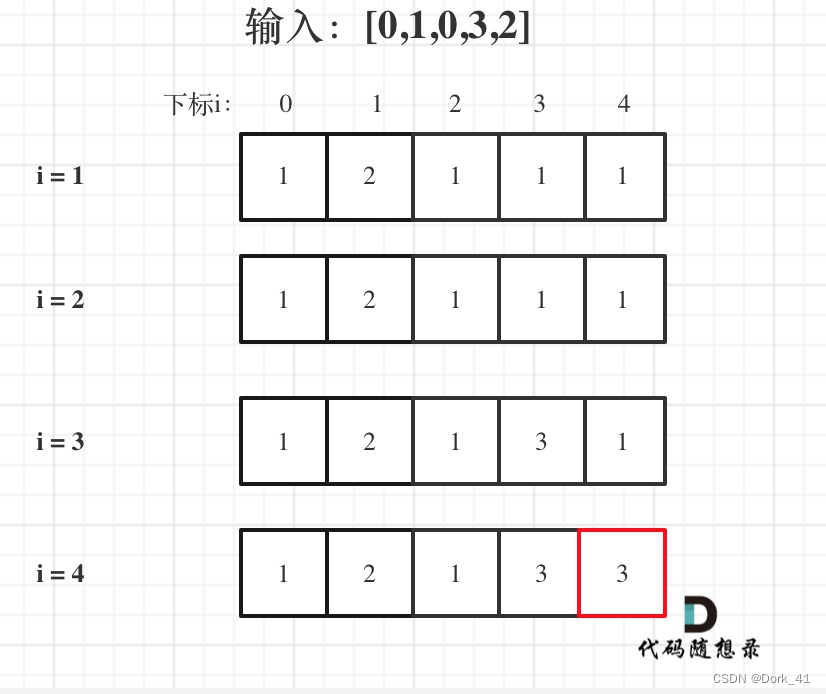
dp[i] 為下標范圍為0到i+1之間,最長的自增序列的長度。
2. 確定遞推公式
因為本題規定了自增序列可以不連續,所以我們不能只和前一個元素對比,而是和所有前面的元素對比,如果大于前面的某個元素,就在那個元素的基礎上+1,當然我們要一直保留最大值。
所以dp[i] = max(dp[j] + 1, dp[i])
其中i是當前元素,j是i之前的某個元素。
3. dp數組初始化
因為我們要返回的是長度,而每個元素單獨長度已經為1了,所以所有元素都先初始化為1。
4. 確定遍歷順序
遞推公式中的j是i之前的元素下標,所以從前往后遞推。
5. 舉例
674.?最長連續遞增序列
class Solution:def findLengthOfLCIS(self, nums: List[int]) -> int:n = len(nums)dp = [1] * nfor i in range(1, n):if nums[i] > nums[i-1]:dp[i] = dp[i-1] + 1return max(dp)- 時間復雜度:O(n)
- 空間復雜度:O(n)
上一道題的簡化版,不太清楚為什么卡哥為什么設置先做上道題再做這道題。
唯一區別是這次要求的是連續數組,但其實這個條件簡化了遍歷和遞推公式,因為我們不用再使用雙循環遍歷當前元素之前的所有元素,而是只對比前一個就可以了。
所以這道題只需要一個循環,每個當前元素 i 只需和 i-1 對比即可。
718.?最長重復子數組?
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]res = 0for i in range(1, len(nums1) + 1):for j in range(1, len(nums2) + 1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1res = max(res, dp[i][j])return res- 時間復雜度:O(n^2)
- 空間復雜度:O(n^2)
1. 確定dp數組的含義
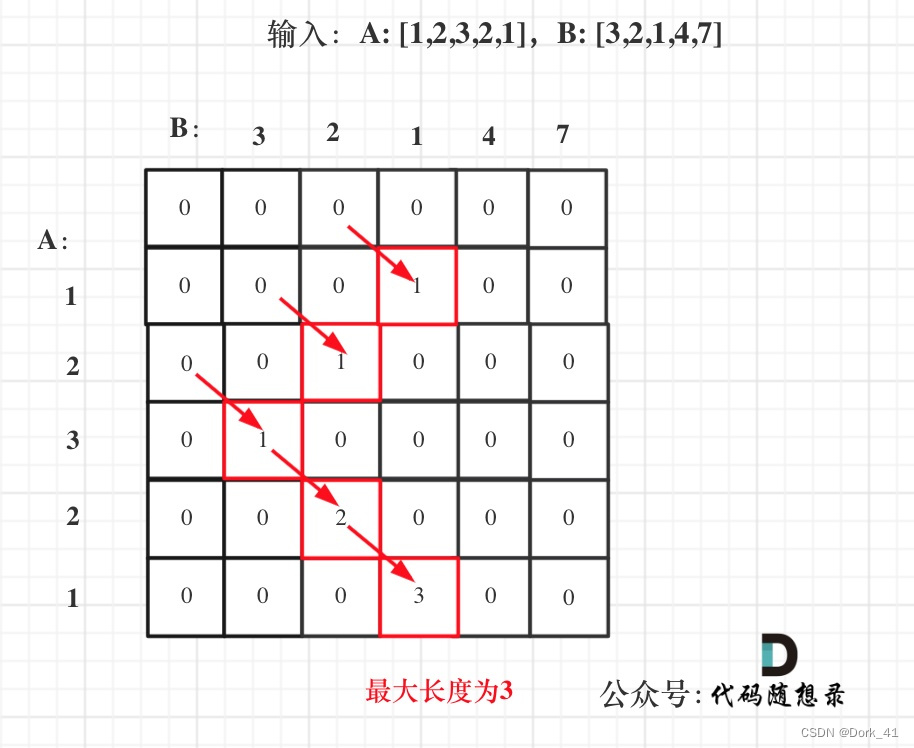
dp[i][j] :以下標i - 1為結尾的A,和以下標j - 1為結尾的B,最長重復子數組長度為dp[i][j]。
2. 確定遞推公式
根據dp[i][j]的定義,dp[i][j]的狀態只能由dp[i - 1][j - 1]推導出來。
即當A[i - 1] 和B[j - 1]相等的時候,dp[i][j] = dp[i - 1][j - 1] + 1;
3. dp數組初始化
但dp[i][0] 和dp[0][j]要初始值,因為 為了方便遞歸公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化為0。
4. 確定遍歷順序
外層for循環遍歷A,內層for循環遍歷B,反過來也可以。
同時題目要求長度最長的子數組的長度。所以在遍歷的時候順便把dp[i][j]的最大值記錄下來。
5. 舉例

)







)
期末復習)

)


![跳躍游戲[中等]](http://pic.xiahunao.cn/跳躍游戲[中等])



