Logistic 回歸 概述

Logistic 回歸 或者叫邏輯回歸 雖然名字有回歸，但是它是用來做分類的。其主要思想是: 根據現有數據對分類邊界線(Decision Boundary)建立回歸公式，以此進行分類。

須知概念

Sigmoid 函數

回歸 概念

假設現在有一些數據點，我們用一條直線對這些點進行擬合（這條直線稱為最佳擬合直線），這個擬合的過程就叫做回歸。進而可以得到對這些點的擬合直線方程，那么我們根據這個回歸方程，怎么進行分類呢？請看下面。

二值型輸出分類函數

我們想要的函數應該是: 能接受所有的輸入然后預測出類別。例如，在兩個類的情況下，上述函數輸出 0 或 1.或許你之前接觸過具有這種性質的函數，該函數稱為 海維塞得階躍函數(Heaviside step function)，或者直接稱為 單位階躍函數。然而，海維塞得階躍函數的問題在于: 該函數在跳躍點上從 0 瞬間跳躍到 1，這個瞬間跳躍過程有時很難處理。幸好，另一個函數也有類似的性質（可以輸出 0 或者 1 的性質），且數學上更易處理，這就是 Sigmoid 函數。 Sigmoid 函數具體的計算公式如下:

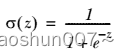
下圖給出了 Sigmoid 函數在不同坐標尺度下的兩條曲線圖。當 x 為 0 時，Sigmoid 函數值為 0.5 。隨著 x 的增大，對應的 Sigmoid 值將逼近于 1 ; 而隨著 x 的減小， Sigmoid