84.柱狀圖中最大的矩形

力扣題目鏈接(opens new window)

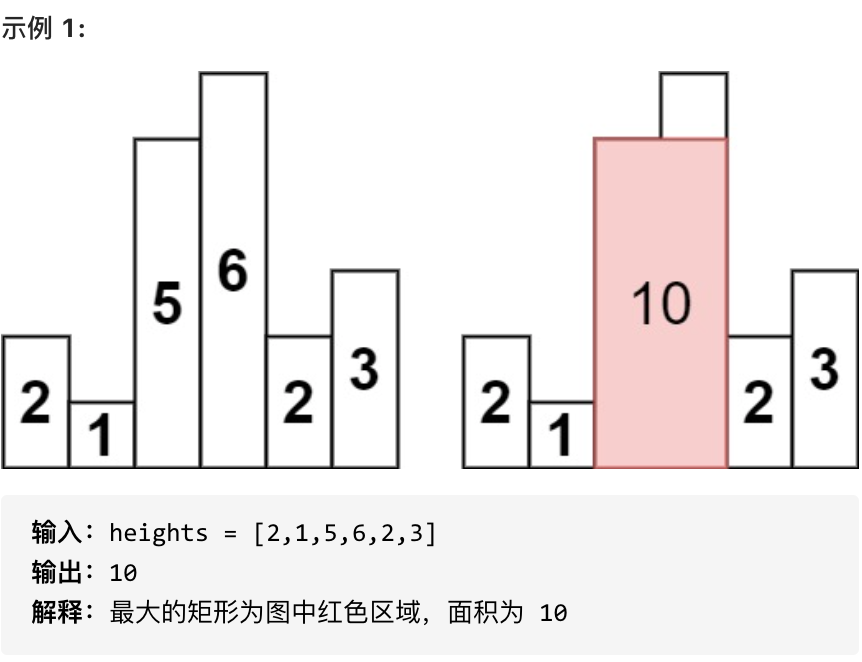
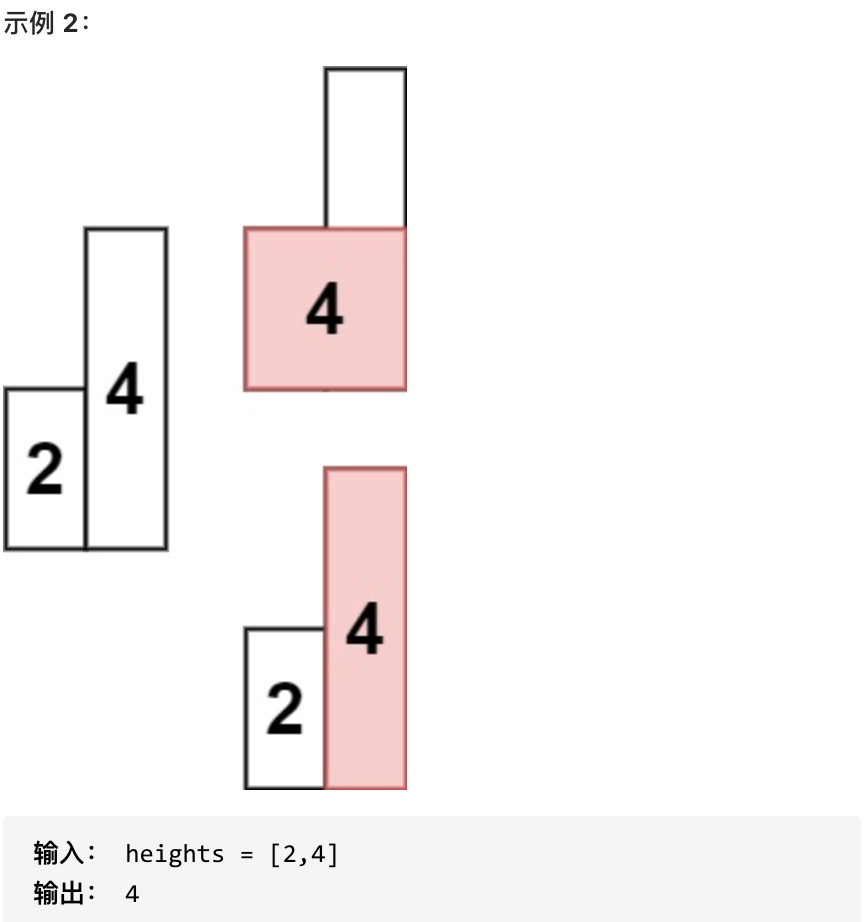
給定 n 個非負整數，用來表示柱狀圖中各個柱子的高度。每個柱子彼此相鄰，且寬度為 1 。

求在該柱狀圖中，能夠勾勒出來的矩形的最大面積。

• 1 <= heights.length <=10^5
• 0 <= heights[i] <= 10^4

1. 初始化棧和最大面積變量:

   • 創建一個空棧 stack 來存儲柱子的索引。
   • 初始化一個變量 max_area 用于存儲遍歷過程中計算出的最大面積。

2. 處理每個柱子:

   • 遍歷每個柱子的高度 heights，同時在 heights 的末尾添加一個高度為 0 的柱子，以確保棧中的所有柱子都能被處理。
   • 對于每個柱子 i：
     • 當棧不為空且當前柱子的高度 heights[i] 小于棧頂柱子的高度時，執行以下操作：
       • 彈出棧頂元素，該元素索引記為 top。這意味著以 heights[top] 為高的矩形的右邊界已經確定。
       • 計算矩形的寬度：
         • 如果棧為空，寬度即為當前柱子的索引 i（因為左邊界是起始位置）。
         • 如果棧不為空，寬度為 i - stack[-1] - 1（當前索引減去新的棧頂元素索引，減去1表示兩個柱子間的距離）。
       • 計算矩形面積：heights[top] * 寬度，并更新 max_area。
     • 將當前柱子索引 i 壓入棧中。

3. 返回最大面積:

   • 經過上述遍歷，我們已經計算出了每個可能的矩形的面積，并記錄了其中的最大值。
   • 返回 max_area 作為結果。

?

class Solution:def largestRectangleArea(self, heights):stack = []max_area = 0heights.append(0)  # 添加一個高度為0的柱子，確保所有柱子都被彈出for i, h in enumerate(heights):while stack and heights[stack[-1]] > h:height = heights[stack.pop()]width = i if not stack else i - stack[-1] - 1max_area = max(max_area, height * width)stack.append(i)return max_area# solution = Solution()
# example_heights = [2, 1, 5, 6, 2, 3]
# result = solution.largestRectangleArea(example_heights)
# print(result)