
Hi, 你好。我是茶桁。
前面幾節課中,我們從最初的理解神經網絡,到講解函數,多層神經網絡,拓樸排序以及自動求導。 可以說,最難的部分已經過去了,這節課到了我們來收尾的階段,沒錯,生長了這么久,終于到迎接成果的時候了。
好,讓我們開始。
我們還是用上一節課的代碼:
21.ipynb。
我們上一節課中,實現了自動計算的部分。
for node in sorted_nodes[::-1]:print('\n{}'.format(node.name))node.backward()
結果我就不打印了,節省篇幅。
那我們到這一步之后,咱們就已經獲得了偏導,現在要考慮的問題就是去更新它,去優化它的值。
learning_rate = 1e-5for node in sorted_nodes:node.value = node.value + -1 * node.gradients[node] * learning_rate
node的值去更新,就應該等于它本身的值加上一個-1乘以它的偏導在乘以一個learning_rate, 我們對這個是不是已經很熟悉了?我們從第8節線性回歸的時候就一直在接觸這個公式。
只不過在這個地方,x, y的值也要更新嗎? 它們的值是不應該去更新的,那要更新的應該是k, b的值。
那么在這個地方該怎么辦呢?其實很簡單,我們添加一個判斷就可以了:
for node in sorted_nodes:if node.is_trainable:node.value = node.value + -1 * node.gradients[node] * learning_rate
然后我們給之前定義的類上加一個變量用于判斷。
class Node:def __init__(..., is_trainable=False):...self.is_trainable = is_trainable在這里我們默認是不可以訓練的,只有少數的一些是需要訓練的。
然后我們在初始化的部分把這個定義的值加上:
node_k = Placeholder(name='k', is_trainable=True)
node_b = Placeholder(name='b', is_trainable=True)
對了,我們還需要將Placeholder做些改變:
class Placeholder(Node):def __init__(..., is_trainable=False):Node.__init__(.., is_trainable=is_trainable)......
這就意味著,運行for循環的時候只有k和b的值會更新,我們再加幾句話:
for node in sorted_nodes:if node.is_trainable:...cmp = 'large' if node.gradients[node] > 0 else 'small'print('{}的值{},需要更新。'.format(node.name, cmp))---
k的值small,需要更新。
b的值small,需要更新。
我們現在將forward, backward和optimize的三個循環封裝乘三個方法:
def forward(graph_sorted_nodes):# Forwardfor node in sorted_nodes:node.forward()def backward(graph_sorted_nodes):# Backwardfor node in sorted_nodes[::-1]:print('\n{}'.format(node.name))node.backward()def optimize(graph_sorted_nodes, learning_rate=1e-3):# optimizefor node in sorted_nodes:if node.is_trainable:node.value = node.value + -1 * node.gradients[node] * learning_ratecmp = 'large' if node.gradients[node] > 0 else 'small'print('{}的值{},需要更新。'.format(node.name, cmp))然后我們再來定義一個epoch方法,將forward和backward放進去一起執行:
def run_one_epoch(graph_sorted_nodes):forward(graph_sorted_nodes)backward(graph_sorted_nodes)
這樣,我們完成一次完整的求值-求導-更新,就可以寫成這樣:
run_one_epoch(sorted_nodes)
optimize(sorted_nodes)
為了更好的觀察,我們將所有的print都刪掉,然后在backward方法中寫一個觀察loss的打印函數:
def backward(graph_sorted_nodes):# Backwardfor node in sorted_nodes[::-1]:if isinstance(node, Loss):print('loss value: {}'.format(node.value))node.backward()
然后我們來對剛才完整的過程做個循環:
# 完整的一次求值-求導-更新:
for _ in range(10):run_one_epoch(sorted_nodes)optimize(sorted_nodes, learning_rate=1e-1)---
loss value: 0.12023025149136042
loss value: 0.11090709486917472
loss value: 0.10118818479676453
loss value: 0.09120180962480523
loss value: 0.08111466190584131
loss value: 0.0711246044819575
loss value: 0.061446239826641165
loss value: 0.05229053883349982
loss value: 0.043842158831920566
loss value: 0.036239620745126
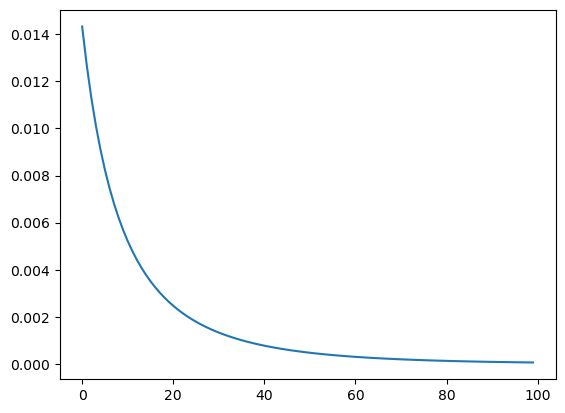
可以看到loss在一點點的下降。當然,這樣循環10次我們還能觀察出來,但是我們如果要成百上千次的去計算它,這樣可就不行了, 那我們需要將history存下來,然后用圖來顯示出來:
loss_history = []
for _ in range(100):..._loss_node = sorted_nodes[-1]assert isinstance(_loss_node, Loss)loss_history.append(_loss_node.value)optimize(sorted_nodes, learning_rate=1e-1)plt.plot(loss_history)
我們現在可以驗證一下,我們擬合的yhat和真實的y之間差距有多大,首先我們當然是要獲取到每個值的下標,然后用sigmoid函數來算一下:
sorted_nodes---
[k, y, x, b, Linear, Sigmoid, Loss]
通過下標來進行計算, k是0, x是2, b是3, y是1:
def sigmoid(x):return 1/(1+np.exp(-x))# k*x+b
sigmoid_x = sorted_nodes[0].value * sorted_nodes[2].value + sorted_nodes[3].value
print(sigmoid(sigmoid_x))# y
print(sorted_nodes[1].value)---
0.891165479601981
0.8988713384533658
可以看到,非常的接近。那說明我們擬合的情況還是不錯的。
好,這里總結一下,就是我們有了拓樸排序,就能向前去計算它的值,通過向前計算的值就可以向后計算它的值。那現在其實我們已經完成了一個mini的深度學習框架的核心內容,咱們能夠定義節點,能夠前向傳播運算,能夠反向傳播運算,能更新梯度了。
那接下來是不是就結束了呢?很遺憾,并沒有,接著咱們還要考慮如何處理多維數據。咱們現在看到的數據都是x、k、b的輸入,也就是都是一維的。
然而咱們真實世界中大多數場景下其實都是多維度的,其實都是多維數組。那么多維數組的還需要更新些什么,和現在有什么區別呢?
我們來接著往后看,因為基本上寫法和現在這些幾乎完全一樣,那我也就不這么細致的講了。
為了和之前代碼做一個區分,所以我將多維向量計算的代碼從新開了個文件,放在了23.ipynb里,小伙伴可以去下載到本地研習。
那么多維和現在最大的區別在哪里呢?就在于計算的時候,我們就要用到矩陣運算了。只是值變成了矩陣,運算變成的了矩陣運算。好,我們從Node開始來改動它,沒什么變化的地方我就直接用...來省略了:
class Node:def __init__(self, input=[]):...def forward(self):raise NotImplementeddef backward(self):raise NotImplementedclass Placeholder(Node):def __init__(self):Node.__init__(self)def forward(self, value=None):...def backward(self):self.gradients = {self:0}for n in self.outputs:grad_cost = n.gradients[self]self.gradients[self] = grad_cost * 1class Linear(Node):def __init__(self, x, k, b):...def forward(self):...def backward(self):self.gradients = {n: np.zeros_like(n.value) for n in self.inputs}for n in self.outputs:grad_cost = n.gradients[self]self.gradients[self.inputs[0]] = np.dot(grad_cost, self.inputs[1].value.T)self.gradients[self.inputs[1]] = np.dot(self.inputs[0].value.T, grad_cost)self.gradients[self.inputs[2]] = np.sum(grad_cost, axis=0, keepdims=False)class Sigmoid(Node):def __init__(self, node):Node.__init__(self, [node])def _sigmoid(self, x):...def forward(self):...def backward(self):self.partial = self._sigmoid(self.x) * (1 - self._sigmoid(self.x))self.gradients = {n: np.zeros_like(n.value) for n in self.inputs}for n in self.outputs:grad_cost = n.gradients[self] self.gradients[self.inputs[0]] = grad_cost * self.partialclass MSE(Node): # 也就是之前的Loss類def __init__(self, y, a):Node.__init__(self, [y, a])def forward(self):y = self.inputs[0].value.reshape(-1, 1)a = self.inputs[1].value.reshape(-1, 1)assert(y.shape == a.shape)self.m = self.inputs[0].value.shape[0]self.diff = y - aself.value = np.mean(self.diff**2)def backward(self):self.gradients[self.inputs[0]] = (2 / self.m) * self.diffself.gradients[self.inputs[1]] = (-2 / self.m) * self.diff
類完成之后,我們還有一些其他的方法:
def forward_and_backward(graph): # run_one_epochfor n in graph:n.forward()for n in graph[::-1]:n.backward()
def toplogic(graph):...
def convert_feed_dict_to_graph(feed_dict):...
# 將sorted_nodes賦值從新定義了一個方法
def topological_sort_feed_dict(feed_dict):graph = convert_feed_dict_to_graph(feed_dict)return toplogic(graph)def optimize(trainables, learning_rate=1e-2):for node in trainables:node.value += -1 * learning_rate * node.gradients[node]
這樣就完成了。可以發現基本上代碼沒有什么變動,變化比較大的都是各個類中的backward方法,因為要將其變成使用矩陣運算。
我們來嘗試著用一下這個多維算法,我們還是用波士頓房價的那個數據來做一下嘗試:
X_ = data['data']
y_ = data['target']# Normalize data
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis=0)n_features = X_.shape[1]
n_hidden = 10
W1_ = np.random.randn(n_features, n_hidden)
b1_ = np.zeros(n_hidden)
W2_ = np.random.randn(n_hidden, 1)
b2_ = np.zeros(1)# Neural network
X, y = Placeholder(), Placeholder()
W1, b1 = Placeholder(), Placeholder()
W2, b2 = Placeholder(), Placeholder()l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(y, l2)feed_dict = {X: X_,y: y_,W1: W1_,b1: b1_,W2: W2_,b2: b2_
}epochs = 5000
# Total number of examples
m = X_.shape[0]
batch_size = 16
steps_per_epoch = m // batch_sizegraph = topological_sort_feed_dict(feed_dict)
trainables = [W1, b1, W2, b2]print("Total number of examples = {}".format(m))
我們在中間定義了l1, s1, l2, cost, 分別來實例化四個類。然后我們就需要根據數據來進行迭代計算了,定義一個losses來保存歷史數據:
losses = []epochs = 100for i in range(epochs):loss = 0for j in range(steps_per_epoch):# Step 1X_batch, y_batch = resample(X_, y_, n_samples=batch_size)X.value = X_batchy.value = y_batch# Step 2forward_and_backward(graph) # set output node not important.# Step 3rate = 1e-2optimize(trainables, rate)loss += graph[-1].valueif i % 100 == 0: print("Epoch: {}, Loss: {:.3f}".format(i+1, loss/steps_per_epoch))losses.append(loss/steps_per_epoch)---
Epoch: 1, Loss: 194.170
...
Epoch: 4901, Loss: 3.137
可以看到它loss下降的非常快,還記得咱們剛開始的時候在訓練波士頓房價數據的時候,那個loss下降到多少? 最低是不是就下降到在第一節課的時候我們的lose最多下降到了多少47.34對吧?那現在呢?直接下降到了3,這是為什么? 因為我們的維度多了,維度多了它就準確了。這說明什么? 說明大家去談戀愛的時候,不要盯著對象的一個方面,多方面考察,才能知道這個人是否合適。
好,現在看起來效果是很好,但是我們想知道到底擬合出來的什么函數,那怎么辦?咱們把這個維度降低成三維空間就可以看了。
現在咱們這個波士頓的所有數據實際上是一個15維的數據,15維的數據你根本看不了,咱們現在只要把x這個里邊取一點值,在這個里邊稍微把值給它變一下。
X_ = dataframe[['RM', 'LSTAT']]
y_ = data['target']
在咱們之前的課程中對其進行計算的時候就分析過,RM和LSTAT是影響最大的兩個特征,我們還是來用這個。然后我們將剛才的代碼從新運行一遍:
losses = []for i in tqdm_notebook(range(epochs)):...---
Epoch: 1, Loss: 150.122
...
Epoch: 4901, Loss: 16.181
這次下降的就沒上次好了。
現在我們可視化一下這個三維空間來看看:
from mpl_toolkits.mplot3d import Axes3Dpredicate_results = []
for rm, ls in X_.values:X.value = np.array([[rm, ls]])forward_and_backward(graph)predicate_results.append(graph[-2].value[0][0])%matplotlib widgetfig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')X_ = dataframe[['RM', 'LSTAT']].values[:, 0]
Y_ = dataframe[['RM', 'LSTAT']].values[:, 1]Z = predicate_resultsrm_and_lstp_price = ax.plot_trisurf(X_, Y_, Z, color='green')ax.set_xlabel('RM')
ax.set_ylabel('% of lower state')
ax.set_zlabel('Predicated-Price')
然后我們就能看到一個數據的三維圖形,因為我們開啟了widget, 所以可以進行拖動。
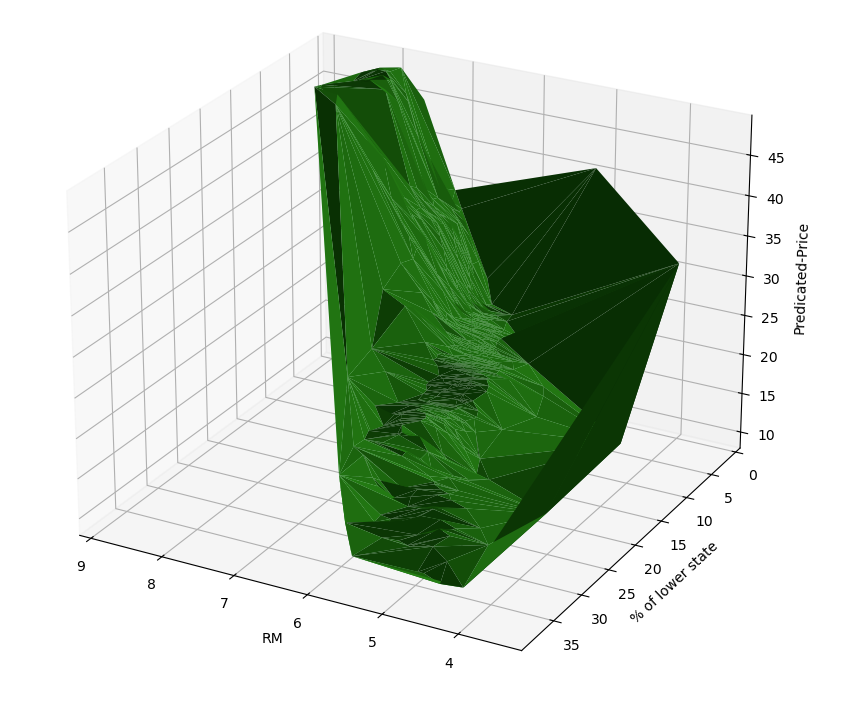

從圖形上看,確實符合房間越多,低收入人群越少,房價越高的特性。
那現在計算機確實幫我們自動的去找到了一個函數,這個函數到底怎么設置咱們都不用關心,它自動就給你求解出來,這個就是深度學習的意義。咱們經過這一系列寫出來的東西其實就已經能夠做到。
我覺得這個真的有一種數學之美,它從最簡單的東西出發,最后做成了這樣一個復雜的東西。確實很深其,并且還都在我們的掌握之中。
好,大家下來以后記得要多多自己敲代碼,多分析其中的一些過程和原理。









)

)


![Java接口自動化測試系列[V1.0.0][概述]](http://pic.xiahunao.cn/Java接口自動化測試系列[V1.0.0][概述])




