機器學習算法(1)——簡單線性回歸

一、說明

????????在在這篇文章中，我們將學習我們的第一個機器學習算法，稱為簡單線性回歸。這是一個重要的算法，因為當您可能正在學習第一個神經網絡（稱為人工神經網絡）時，在此算法中學習的技術也適用于深度學習。我會嘗試將其分解為單獨的模塊，以便您可以更好地理解它（所以這是機器學習系列的第 1 部分）。線性回歸，顧名思義，在監督機器學習中，回歸問題陳述肯定可以借助類似的線性回歸來解決。現在簡單的線性回歸算法到底是什么，假設我有一個數據集，并且這個特定的數據集具有體重和高度等特征。

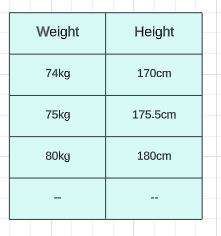
????????假設體重在74 公斤左右，我的身高可能是170 厘米，如果體重在80 公斤左右，我的身高可能是180 厘米，如果體重在75 公斤左右，我的身高可能是175.5 厘米。假設在這種數據集中，我們的主要目標是每當我們給出新的權重時訓練一個模型，該模型應該能夠預測高度，現在你看到這個特征基本上是我們的獨立特征（權重）并且這個特征特別是關于輸出或依賴特征。這就是我們計劃做的，我們將在簡單線性回歸的幫助下進行訓練。那么為什么我們把它說成簡單的線性回歸，這樣通過查看這個你就可以了解這里有多少輸入特征呢？我們有一個輸入特征和一個輸出特征。每當我們有這一輸入特征時，我們就說它是簡單線性回歸。如果我們有多個輸入特征，那么我們可以將其稱為多元線性回歸。因此，在本教程中，我們嘗試指定一個模型，并使用特定數據對其進行訓練，稍后該模型應該能夠預測高度。

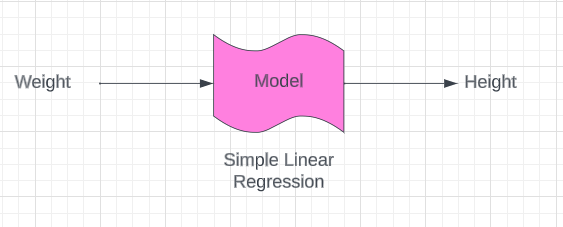
????????因此，關于這個特定的數據集，讓我繪制一些點。假設有一些點是這樣繪制的，因此在回歸的幫助下，我們要做的是創建一條最佳擬合線，而這條最佳擬合線實際上有助于預測權重。因此，讓我們說一下，一旦我們獲得這條最佳擬合線，預測將如何發生，并且應該以您知道真實點之間的距離的方式創建這條最佳擬合線。

????????真實點是指我的數據的輸出，即 170 厘米、180 厘米和 175.5 厘米。這些預測點之間的距離基本上就是誤差。

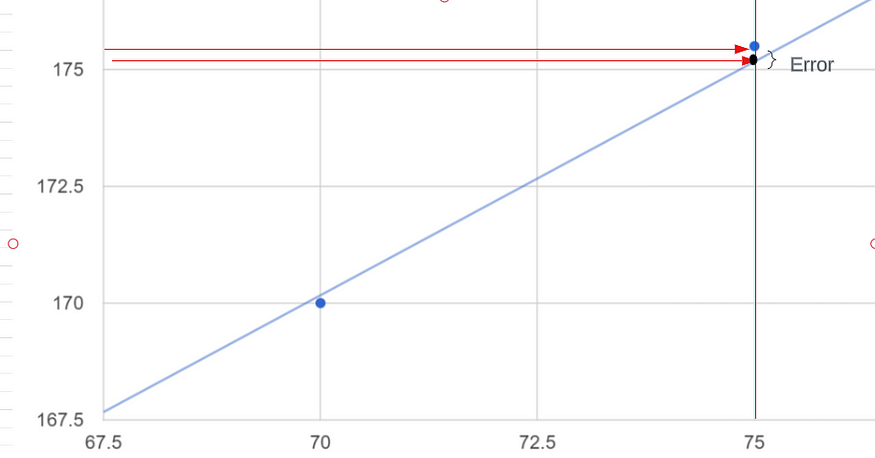
????????所以這些是我的真實點（藍色點），藍色線是使用這些點的預測線。我們只是創建一條預測線，每當我們獲得新的數據點時，它都是最佳擬合線，假設特定的重量為 72.5 公斤，我們如何預測我們的輸出，這意味著高度應該是多少？我們只是從 x 軸到預測線畫一條線，這是我的最佳擬合線，從最佳擬合線我將畫另一條線到我的 y 軸所以這條線符合我在 y 的高度軸是我給定輸入的輸出。

????????這就是我們在簡單線性回歸中所做的。讓我們嘗試了解該特定最佳擬合線的數學方程是什么以及最佳擬合線的具體誤差是什么。在此之前，我們需要了解我在解釋整個機器學習算法時實際上將使用的一些符號。所以我要畫另一張圖，假設這是 x 軸，我的體重在x 軸上，身高在y 軸上，我剛剛隨機創建了一些點，這些點基本上提到了我們的數據集。

????????我將訓練我們的特定模型。我們再次計劃在這里創建一條最適合的生產線。為了創建這條最佳擬合線，我們只需要一些方程，即：

y = mx + c

????????如果您看過一些研究論文，他們也可能會使用類似的內容，

Y = β 0 + β 1 x

????????您可能還見過這樣的方程，

hθ(x)=θ0+θ1x

????????我將使用特定的符號，只不過是hθ(x)=θ0+θ1x。該方程稱為假設，用h(x)=θ0 +θ1x 的形式表示（基本上與 y = mx + c 相同），其中 θ0（或 c）和 θ1 是（或 m）參數。我們希望找到使我們的假設與數據最佳匹配的參數值。現在這里的 X 表示我的獨立特征，即重量。請嘗試理解什么是θ0和什么是θ1。首先，θ0到底是什么，我們說它是一個截距。為什么我們說它是攔截？這是通過簡單的數學計算得出的。假設我的X值為零，那么會發生hθ(x)=θ0。正如您在我的圖表中看到的，最佳擬合線在某處與 y 軸相交。所以我的最佳擬合線與 y 軸相交的點并將其作為攔截器。這意味著當 x 軸為零時，即θ0的值。現在我們知道θ0的含義是什么了。它只不過是一個攔截器。當我們談論斜率或系數時，它表示 x 軸上的唯一運動以及有關 y 軸的運動。

????????這由等式中的θ1表示。假設如果我有許多獨立的特征，那么這個方程就變成了

$h_{\theta }(x)= \theta _0 + \theta _1 x_1 + \theta _2 x_2 + .. + \theta _n x_n$

????????所以最后我們知道我們可以使用這個方程預測給定 x 值的y 值。我們將此預測點表示為?。你知道 y 是我們的實際輸出值。現在我們可以使用這兩個值得到誤差方程。

Error = y - ?

????????現在我們將提出一條最佳擬合線，其中當我嘗試計算或求所有這些誤差的總和時，它應該是最小的。假設存在多條具有不同誤差總和值的最佳擬合線。您必須選擇誤差總和值最小的最佳擬合線。

二、回歸成本函數

????????在這里，我們將找到選擇最佳擬合線的優化方法。為此，我們將使用成本函數。該成本函數以符號形式給出。

????????我們必須創建最佳擬合線，以便我們可以獲得所有特定誤差的總和，并且它應該是最小的。這就是為什么我們以這種特定的方式采用這個成本函數。hθ(x)^i是我的預測點。y?^i是我的真值點/真實輸出。當我們進行減法時，我們可以在這里得到誤差值。

????????我們進行平方的原因是因為我們使用的成本函數技術是均方誤差。是否存在不同類型的成本函數？是的，有平均絕對誤差（MAE）和均方根誤差（RMSE）。

????????θ0表示截距，θ1表示斜率。_?您只需要不斷更改 θ0 和 θ1 值，并嘗試找出誤差最小的最佳擬合線。

????????那么直線方程是什么呢

hθ(x)=θ0+θ1x

????????由此，我將在二維圖中解釋所有這些，以便更好地理解這個理論。所以我假設我的θ0 = 0。那么我的截距將為零，最佳擬合線將穿過原點。現在我可以像這樣創建我的方程。

hθ(x)= θ1x  : because my θ0 = 0

????????我將使用這個方程來獲取 hθ(x) 的值。讓我們考慮這是我的整個數據集，我正在嘗試創建一條最佳擬合線并找到該線的最小誤差。

? ? ? ? 示例數據集

????????讓我們繪制這些數據的圖表。現在我將使用上面的方程來繪制我的最佳擬合線。

? ? ? ? 與實際值的圖表

????????現在我的斜率是 θ1 ，我們假設θ1= 1。稍后，我們將改變斜率以獲得不同的最佳擬合線以最小化誤差。

hθ(x)= θ1x
Let θ1 = 1 (This is my slope value. Assumption this value equals to 1)
Now according to the x values in the data hθ(x) values should be like this,
x =  1 -> hθ(x) =  1 
x =  2->  hθ(x) =  2
x =  3->  hθ(x) =  3

現在我們可以用這些值繪制最佳擬合線，這條線將穿過原點（x = 0，y = 0）。

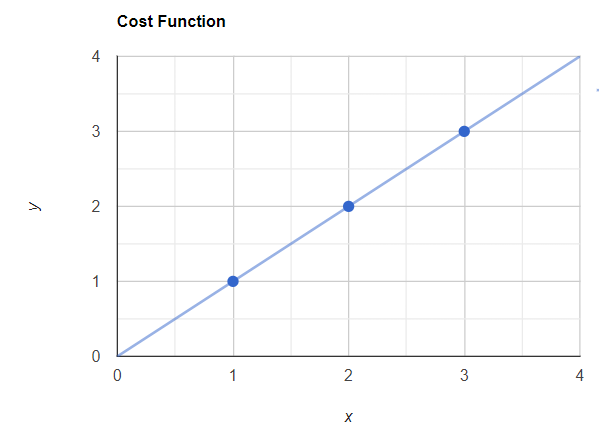
具有實際值和最佳擬合線的圖表

現在你可以看到我的預測點和真實點是重疊的。現在讓我們應用這個成本函數。

Here we assume like θ0 = 0 and the J(θ0, θ1) will be J(θ1) 
Now in the dataset I have 3 points. So that m will be 3. m=3
Now the summation of i =1 to 3 means the entire summation of 1,2 and 3 value.
So I will get the value by expanding this values like this,J(θ1) =  1/2*3 [All 3 dataset Sum (predicted value - actual true value)^2]
J(θ1) =  1/2*3 [ (1 -1)^2 + (2 - 2)^2 + (3 - 3)^2}
J(θ1) = 0

現在您知道 J(θ1) = 0，這意味著沒有錯誤。這是正確的，因為顯然沒有錯誤，因為最佳擬合線通過了所有真實點。

讓我們將斜率值更改為 0.5。

hθ(x)= θ1x
Let θ1 = 0.5(This is my slope value. Assumption this value equals to 0.5)
Now according to the x values in the data hθ(x) values should be like this,
x =  1 -> hθ(x) =  0.5
x =  2->  hθ(x) =  1
x =  3->  hθ(x) =  1.5

現在我們可以用這些值繪制最佳擬合線，這條線將穿過原點（x = 0，y = 0）。

所以這里紅點是我的預測點，藍點是我的實際點。現在讓我們使用 J(θ1) 計算誤差值。

Here we assume like θ0 = 0 and the J(θ0, θ1) will be J(θ1) 
Now in the dataset I have 3 points. So that m will be 3. m=3
Now the summation of i =1 to 3 means the entire summation of 1,2 and 3 value.
So I will get the value by expanding this values like this,J(θ1) =  1/2*3 [All 3 dataset Sum (predicted value - actual true value)^2]
J(θ1) =  1/2*3 [ (0.5 -1)^2 + (1 - 2)^2 + (1.5 - 3)^2}
J(θ1) = 1/2*3 [ (-0.5)^2 + (-1)^2 + (-1.5)^2}
J(θ1) = 0.58

現在我的 J(θ1) 值（誤差）是 0.58。與之前的值相比，這是一個更大的值。

讓我們將斜率值更改為0。

hθ(x)= θ1x
Let θ1 = 0(This is my slope value. Assumption this value equals to 0)
Now according to the x values in the data hθ(x) values should be like this,
x =  1 -> hθ(x) =  0
x =  2->  hθ(x) =  0
x =  3->  hθ(x) =  0

現在我們可以用這些值繪制最佳擬合線，這條線將穿過原點（x = 0，y = 0）。

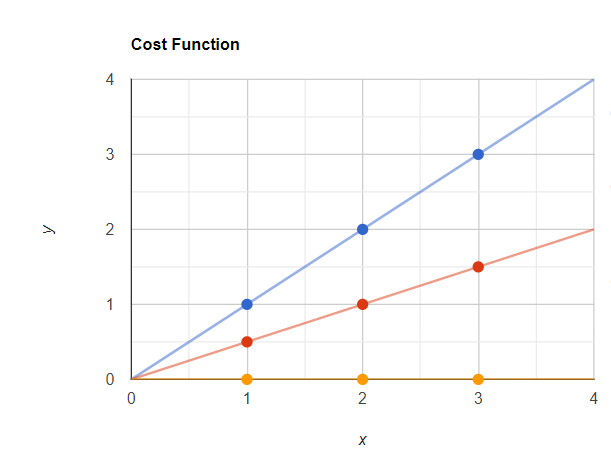
現在我的預測點為黃色，實際點為藍色。現在讓我們使用 J(θ1) 計算誤差值。

Here we assume like θ0 = 0 and the J(θ0, θ1) will be J(θ1) 
Now in the dataset I have 3 points. So that m will be 3. m=3
Now the summation of i =1 to 3 means the entire summation of 1,2 and 3 value.
So I will get the value by expanding this values like this,J(θ1) =  1/2*3 [All 3 dataset Sum (predicted value - actual true value)^2]
J(θ1) =  1/2*3 [ (0 -1)^2 + (0 - 2)^2 + (0 - 3)^2}
J(θ1) = 1/2*3 [ (-1)^2 + (-2)^2 + (-3)^2}
J(θ1) = 2.3

現在讓我們在圖表中繪制這些 J(θ1) 值。看起來像這樣，

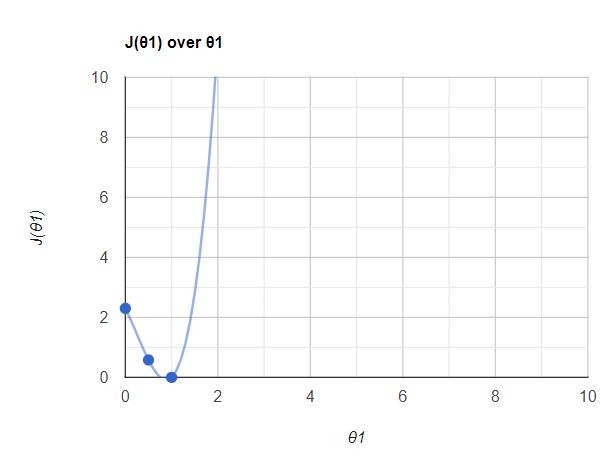
????????所以這里我們使用了 3 個點，當我們使用更多的 J(θ1) 和 θ1 點來繪制時，你會得到這樣的圖。你知道，在 θ1 =1 點，我的誤差非常低。事實上，它是零。所以我們可以說，當我們找到這個θ1值θ1= 1時，我的誤差最小化了。我們將此值稱為全局最小值。總體目標是通過迭代不同的θ值來最小化成本函數。成本函數的最低可能值也稱為全局最小值。最終的線性回歸模型將保留產生最低成本函數的 θ 值。在全局最小值中，我現在將獲得最佳擬合線。

????????所以這整條曲線稱為梯度下降。這對于深度學習技術來說非常重要。

????????所以我希望您能更好地理解簡單線性回歸和回歸成本函數。您將在下一篇文章中了解有關收斂算法的更多信息。