算法的奧秘：種類、特性及應用詳解（算法導論筆記1）

上期總結算法的種類和大致介紹，這一期主要講常見的六種算法詳解以及演示。

排序算法：

排序算法是一類用于對一組數據元素進行排序的算法。根據不同的排序方式和時間復雜度，有多種排序算法。常見的排序算法包括冒泡排序、選擇排序、插入排序、快速排序、歸并排序等。

冒泡排序：通過不斷比較相鄰元素并交換順序，使得較大的元素逐漸“浮”到數組的末尾，如同氣泡一樣。

選擇排序：每次從未排序的元素中選擇最小（或最大）的元素，放到已排序的末尾。

插入排序：將未排序的元素一個個插入到已排序的數組中，從而逐步形成排序好的數組。

快速排序：通過選擇一個基準元素將數組分成兩部分，一部分小于基準元素，一部分大于基準元素，然后遞歸地對這兩部分繼續進行快速排序。

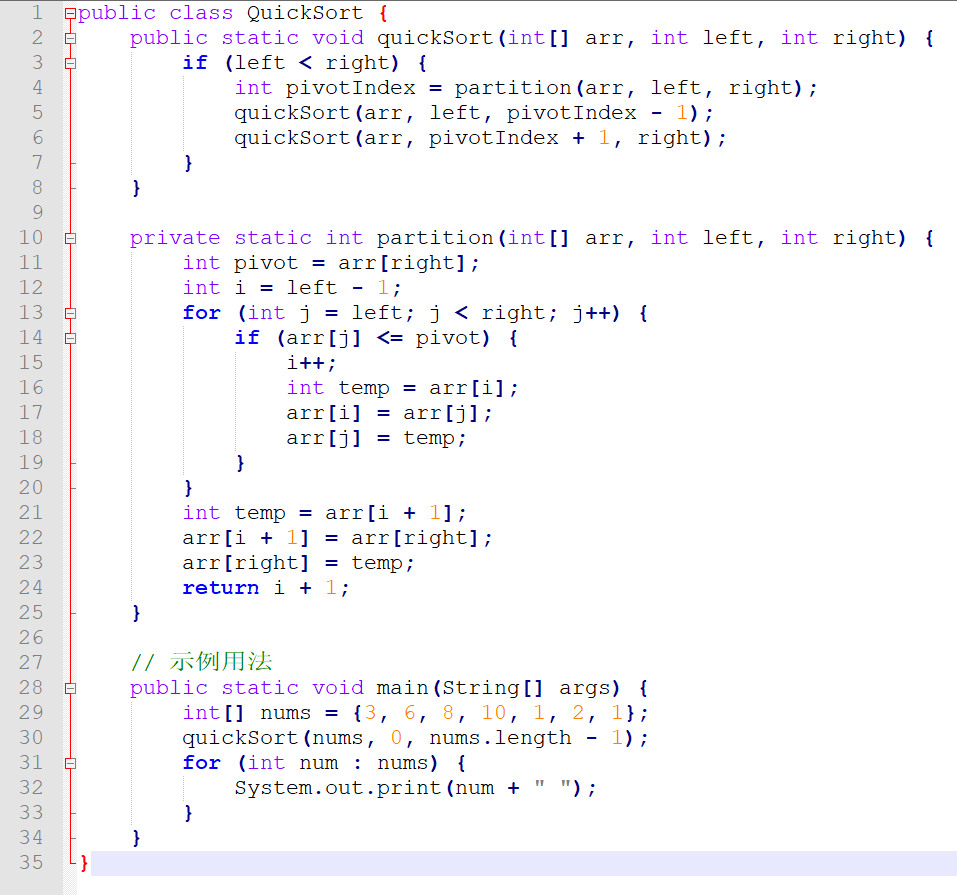
快速排序算法的實現包括兩個主要部分：quickSort和partition。quickSort方法用于遞歸地排序子數組，而partition方法則用于將數組分為兩個子數組，并返回基準元素的索引。在partition方法中，我們選擇數組的最后一個元素作為基準，然后將小于等于基準的元素移到左邊，大于基準的元素移到右邊。最后，我們返回基準元素的索引，以便在quickSort方法中進一步分割子數組。在示例用法中，我們創建了一個包含七個整數的數組，并對其進行快速排序。

歸并排序：采用分治策略，將數組分成若干個子數組，分別進行排序，最后將排好序的子數組合并成完整的排好序的數組。

查找算法：

查找算法用于在數據結構中查找特定元素。常見的查找算法包括線性查找和二分查找等。

線性查找：從數據結構的一端開始逐個比較每個元素，直到找到目標元素或遍歷完整個數據結構。

二分查找：在有序的數據結構中，通過不斷縮小查找范圍來進行查找。首先確定查找范圍的最左端和最右端，然后根據目標元素與中間元素的比較結果來確定下一步查找的方向，不斷縮小查找范圍直至找到目標元素或確定目標元素不存在為止。

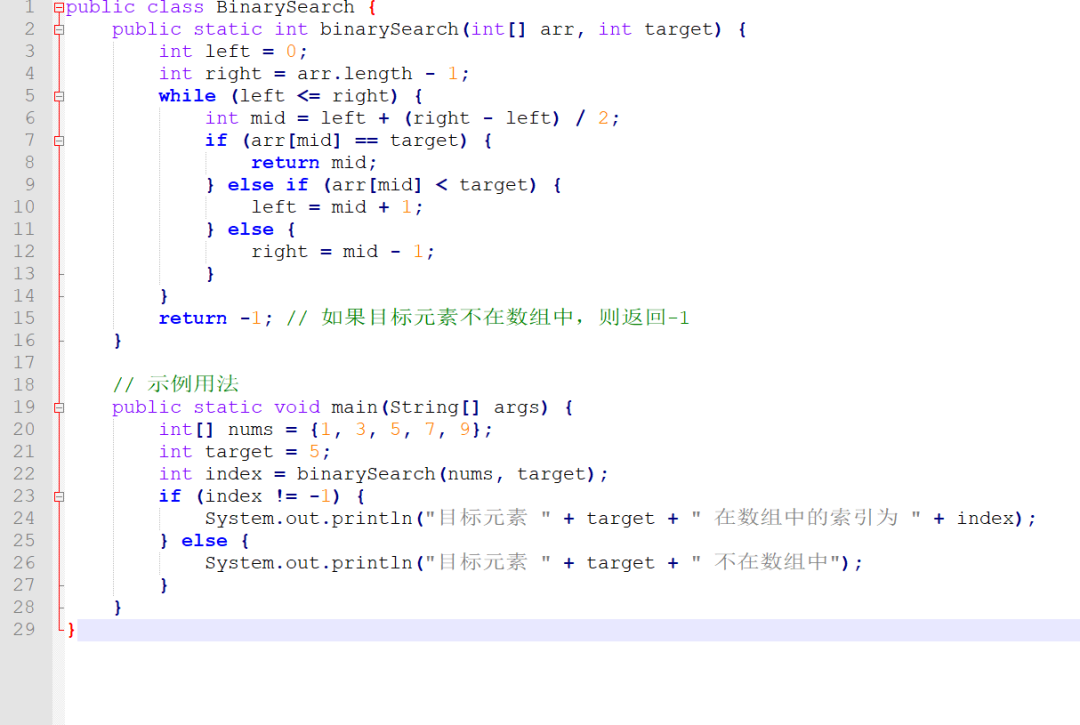
二分查找算法是一種高效的查找算法，它要求待查找的數組必須是有序的。該算法的基本思想是將數組分成兩個部分，然后根據目標元素與中間元素的比較結果，將查找范圍縮小一半。具體來說，我們首先將查找范圍設為整個數組，然后通過比較目標元素與中間元素的大小，不斷將查找范圍縮小，直到找到目標元素或確定目標元素不存在為止。在示例用法中，我們創建了一個包含五個整數的數組，并使用二分查找算法查找目標元素5的位置。如果目標元素存在，則輸出其位置；否則輸出“目標元素不存在”。

圖論算法：

圖論算法用于解決圖論問題，如最短路徑、最小生成樹、網絡流等。常見的圖論算法包括Dijkstra算法、Prim算法、Kruskal算法等。

Dijkstra算法：用于求解單源最短路徑問題，給定一個有向圖和一個起點，求出從起點到圖中所有其他節點的最短路徑。

Prim算法：用于求解最小生成樹問題，在一個無向加權圖中找到一棵包含所有節點且權值和最小的樹。

Kruskal算法：用于求解最小生成樹問題，通過不斷添加邊來構建最小生成樹，直至所有節點都被覆蓋。

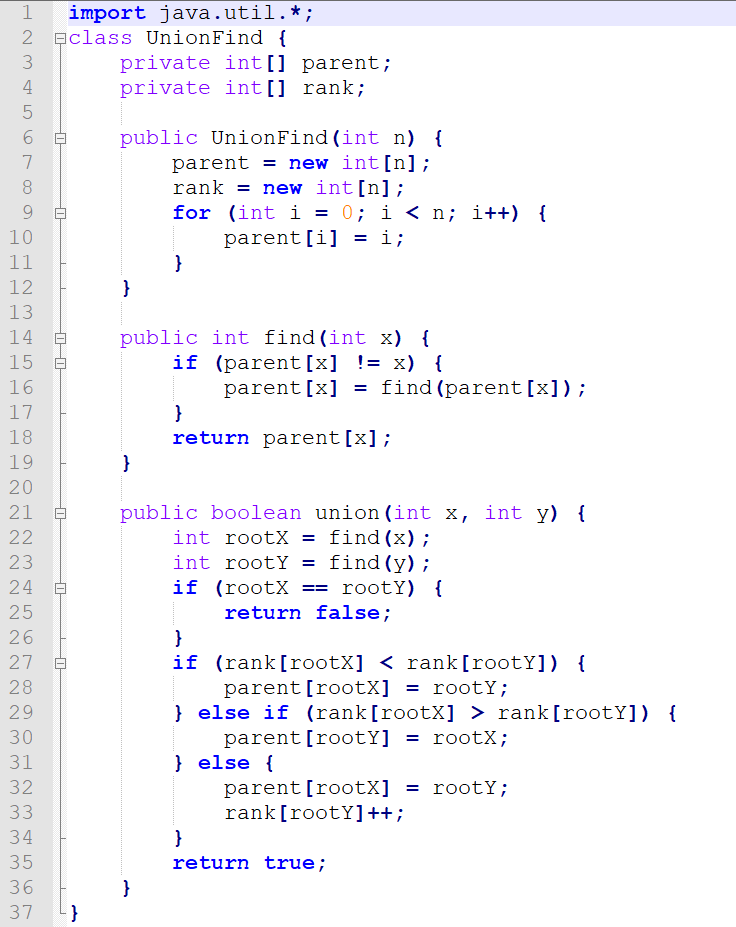
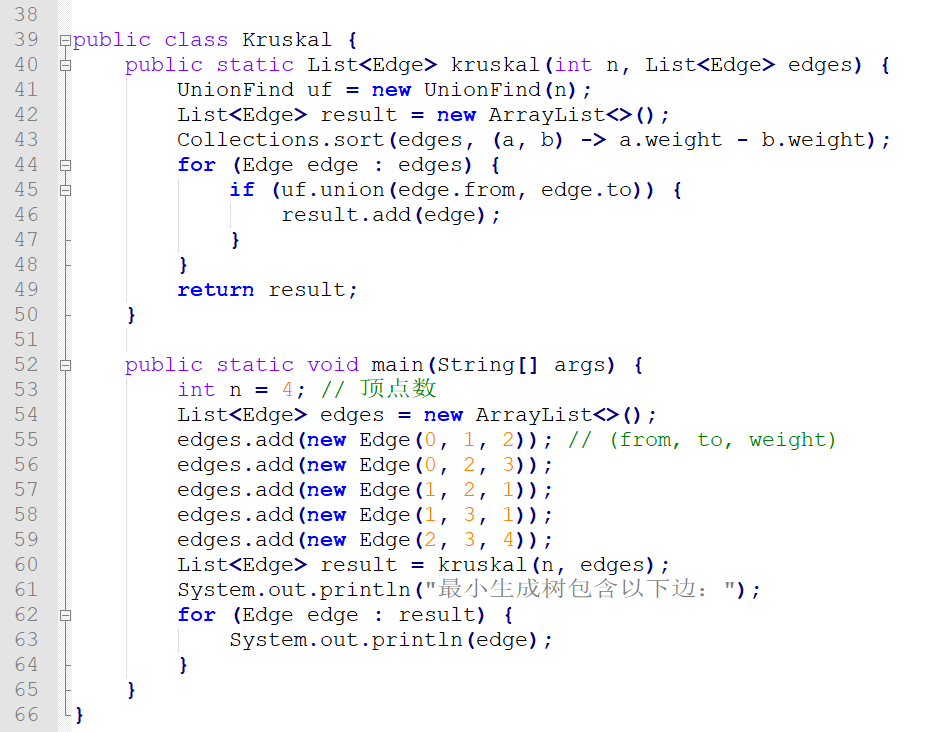
動態規劃算法：

動態規劃算法用于解決最優化問題，通過將問題分解為若干個子問題，并記錄子問題的解，從而避免重復計算，提高求解效率。常見的動態規劃算法包括背包問題、最大子段和問題等。

背包問題：給定一組物品，每種物品都有自己的重量和價值，背包的總容量有限。求解如何選擇物品放入背包使得背包內的總價值最大。
最大子段和問題：給定一個整數數組，求解連續的子數組使得其和最大。

分治算法：

分治算法將問題分解為若干個子問題，分別解決這些子問題，然后將子問題的解合并以得到原問題的解。常見的分治算法包括快速排序、歸并排序等。

快速排序：通過選擇一個基準元素將數組分成兩部分，一部分小于基準元素，一部分大于基準元素，然后遞歸地對這兩部分繼續進行快速排序。最后將排好序的子數組合并成完整的排好序的數組。

歸并排序：采用分治策略，將數組分成若干個子數組

貪心算法：

貪心算法是一種解決問題的策略，它的思想是每一步都選擇當前情況最好或最優（即最有利）的選擇，希望通過這樣的選擇來得到全局最優解。這種算法在每一步中都只考慮當前情況下最好或最優的選擇，而不會考慮這樣的選擇會對后續的結果產生什么樣的影響。

舉個例子來說，比如找零問題：假設我們需要在錢幣面額為100元、50元、20元、10元、5元和1元的錢柜中找零，貪心算法會首先選擇100元的錢幣，然后是50元，以此類推，直到我們找到足夠的零錢。這種策略雖然不一定能找到最優解（即使用最少數量的錢幣），但通常能找到一個接近最優解的結果。

貪心算法的優點在于它每一步的操作都非常簡單明了，也容易實現。同時，由于它每一步都選擇最優解，所以它的時間復雜度通常比較低。但是，貪心算法并不適用于所有問題，有些問題使用貪心算法可能會得到局部最優解，但不一定能得到全局最優解。因此，當我們使用貪心算法時，需要先判斷它是否適用于當前的問題。

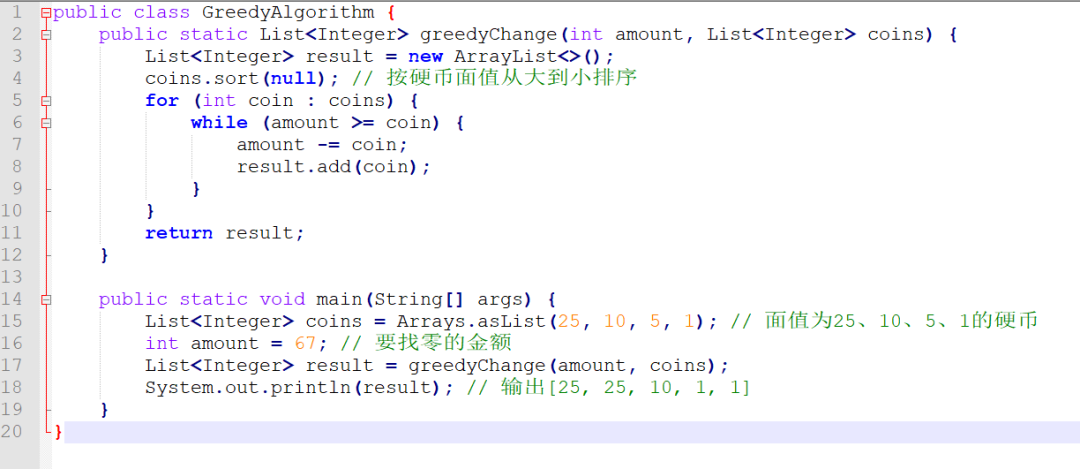
這個算法首先將硬幣按照面值從大到小排序，然后從面值最大的硬幣開始找零，盡可能多地使用這種硬幣，直到找零的金額無法再使用這種硬幣為止。然后，算法使用下一種面值較大的硬幣，重復上述過程，直到找零的金額減到0為止。在實現中，我們將硬幣按照面值從大到小排序，然后依次枚舉每種硬幣，計算使用這種硬幣能夠找零多少金額，然后將這種硬幣加入結果列表中。重復這個過程，直到找零的金額減到0為止。