作者:Benjamin Trent

目前,Lucene 限制 dot_product (點積)?只能在標準化向量上使用。 歸一化迫使所有向量幅度等于一。 雖然在許多情況下這是可以接受的,但它可能會導致某些數據集的相關性問題。 一個典型的例子是 Cohere 構建的嵌入(embeddings)。 它們的向量使用幅度來提供更多相關信息。
那么,為什么不允許點積中存在非歸一化向量,從而實現最大內積呢? 有什么大不了的?
負值和 Lucene 優化
Lucene要求分數非負,因此在析取 (disjunctive query) 查詢中多匹配一個子句只能使分數更高,而不是更低。 這實際上對于動態修剪優化(例如 block-max WAND)非常重要,如果某些子句可能產生負分數,則其效率會大大降低。 此要求如何影響非標準化向量?
在歸一化情況下,所有向量都在單位球面上。 這允許通過簡單的縮放來處理負分數。
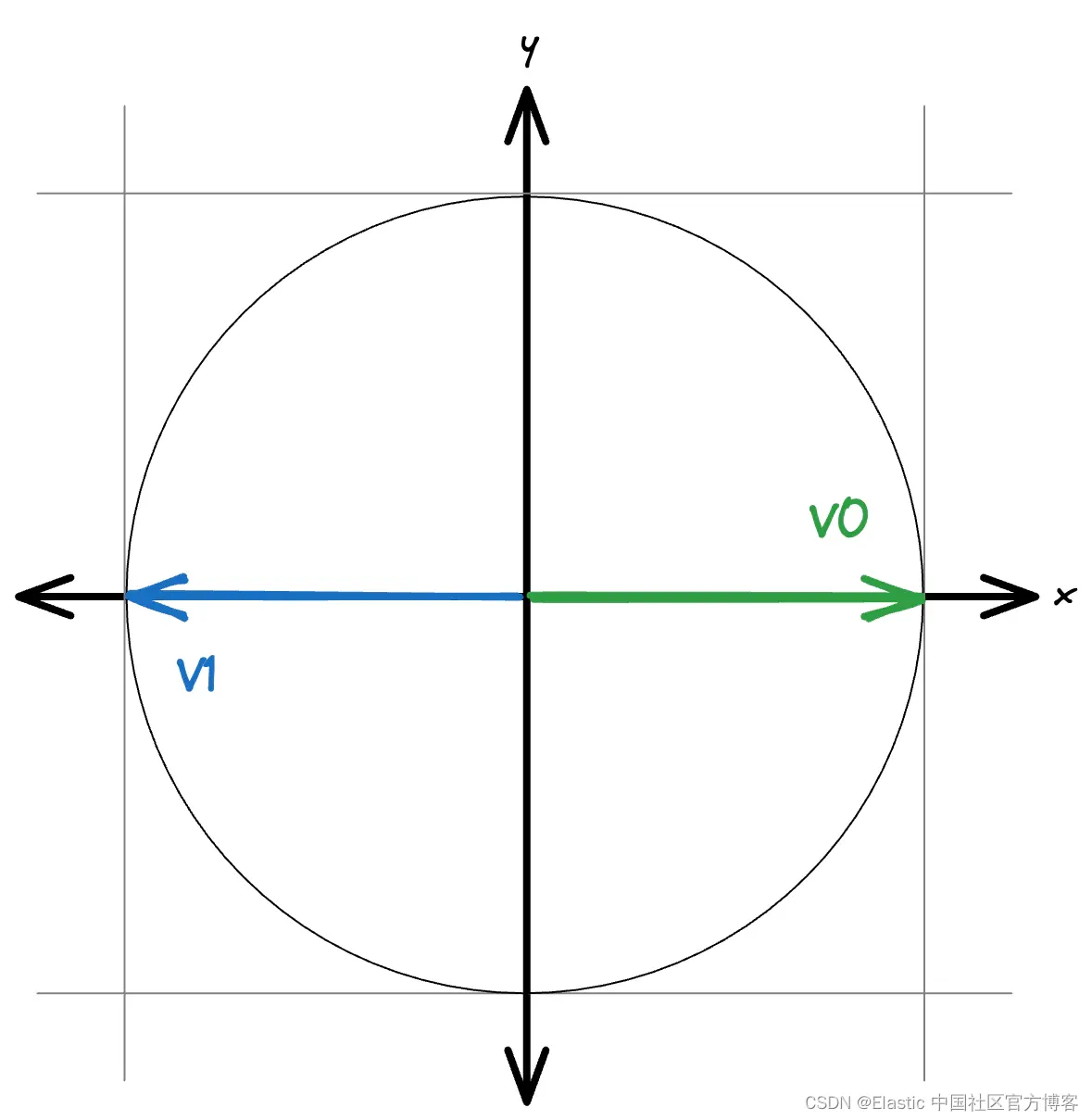
當向量保持其大小時,可能值的范圍是未知的。
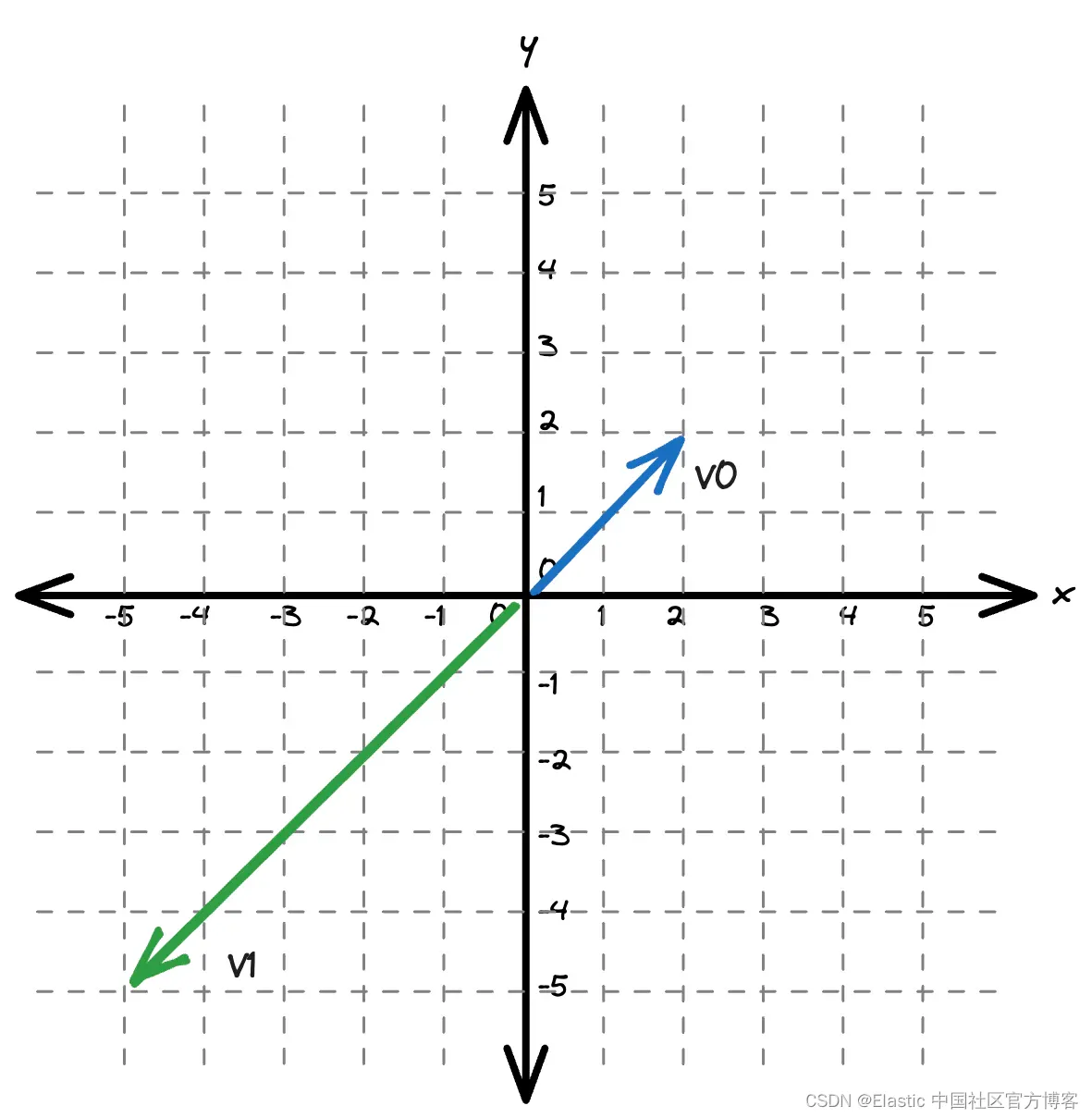
為了允許 Lucene 將 blockMax WAND 與非標準化向量結合使用,我們必須縮放分數。 這是一個相當簡單的解決方案。 Lucene 將使用簡單的分段函數縮放非標準化向量:
if (dotProduct < 0) {return 1 / (1 + -1 * dotProduct);
}
return dotProduct + 1;現在,所有負分數都在 0 -1 之間,所有正分數都在 1 以上。這仍然可以確保較高的值意味著更好的匹配并消除負分數。 很簡單,但這不是最后的障礙。
三角形問題
最大內積不遵循與簡單歐幾里得空間相同的規則。 三角不等式的簡單假設知識被拋棄。 不直觀的是,向量不再最接近其自身。 這可能會令人不安。 Lucene 的向量底層索引結構是分層可導航小世界 (HNSW)。 這是基于圖的算法,它可能依賴于歐幾里得空間假設。 或者在非歐幾里得空間中探索圖會太慢嗎?
一些研究表明,快速搜索需要轉換到歐幾里得空間。 其他人則經歷了更新向量存儲以強制轉換為歐幾里得空間的麻煩。
這導致我們停下來深入挖掘一些數據。 關鍵問題是:HNSW 是否通過最大內積搜索提供良好的召回率和延遲? 雖然 HNSW 最初的論文和其他已發表的研究表明確實如此,但我們需要進行盡職調查。
我們進行的實驗很簡單。 所有的實驗都是在真實數據集或稍微修改的真實數據集上進行的。 這對于基準測試至關重要,因為現代神經網絡創建符合特定特征的向量(請參閱本文第 7.8 節中的討論)。 我們測量了非標準化向量的延遲(以毫秒為單位)與召回率。 將數字與具有相同測量值但采用歐幾里德空間變換的數字進行比較。 在每種情況下,向量都被索引到 Lucene 的 HNSW 實現中,并且我們測量了 1000 次查詢迭代。 每個數據集考慮了三種單獨的情況:按大小順序插入的數據(從小到大)、按隨機順序插入的數據以及按相反順序插入的數據(從大到小)。
以下是 Cohere 真實數據集的一些結果:
 |  |
|
|
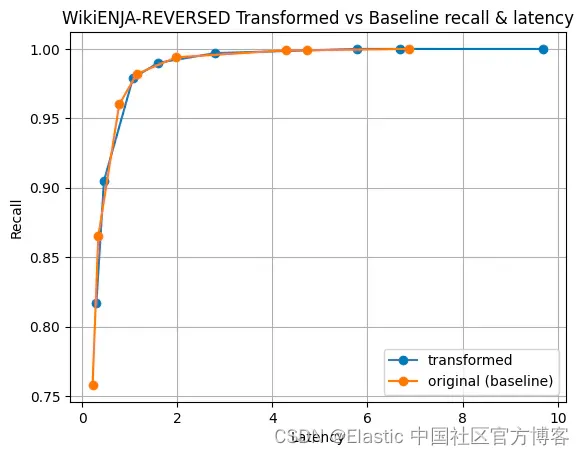 |  |
 |
我們還針對一些合成數據集進行了測試,以確保我們的嚴謹性。 我們使用 e5-small-v2 創建了一個數據集,并通過不同的統計分布縮放了向量的大小。 為了簡潔起見,我將僅顯示兩個分布。
 | 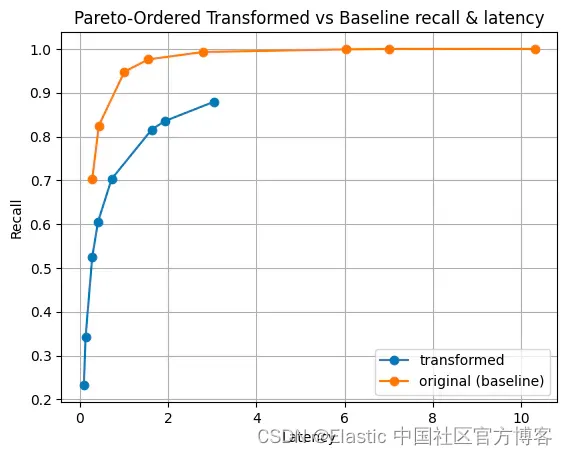 |
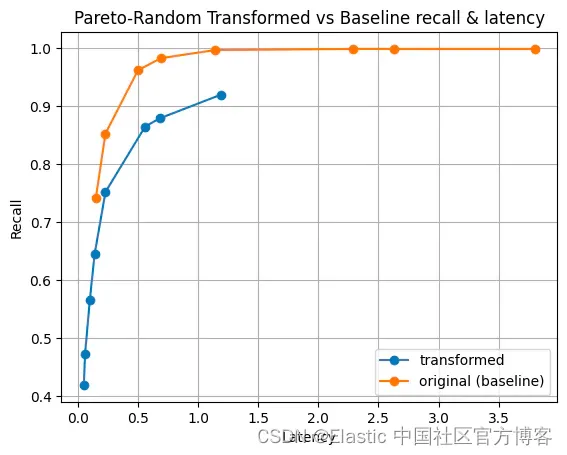 |
圖 6:幅度的伽馬分布。 這種分布可能具有很高的方差,并使其在我們的實驗中獨一無二。
在我們所有的實驗中,唯一需要進行轉換的是使用伽瑪分布創建的合成數據集。 即使這樣,向量也必須以相反的順序插入,首先是最大幅度,以證明變換的合理性。 這些都是例外情況。
如果你想了解所有實驗以及整個過程中的所有錯誤和改進,請參閱 Lucene Github 問題,其中包含所有詳細信息(以及過程中的錯誤)。 這是一個開放式研究和開發的項目!
結論
這是一個相當長的旅程,需要進行多次調查才能確保 Lucene 能夠支持最大內積。 我們相信數據不言自明。 無需進行重大轉換或對 Lucene 進行重大更改。 所有這些工作將很快解鎖 Elasticsearch 的最大內積支持,并允許 Cohere 提供的模型成為 Elastic Stack 中的一等公民。
注:最大內積已經在 8.11 中進行了支持!
原文:Bringing Maximum-Inner-Product into Lucene — Elastic Search Labs












)

 計算兩點云之間的最小距離)

函數)



