發現新天地,歡迎訪問Cr不是鉻的個人網站
引言
與插值問題不同,在擬合問題中不需要曲線一定經過給定的點。擬合問題的目標是尋求一個函數(曲線),使得該曲線在某種準則下與所有的數據點最為接近,即曲線擬合的最好(最小化損失函數)
最小二乘法
在一維線性擬合中,采用的是最小二乘法來求得最優擬合。
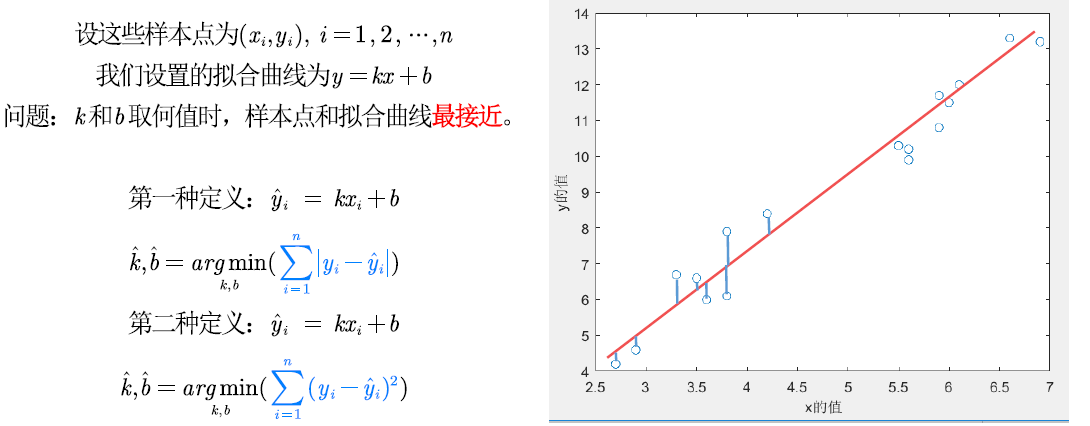
求解過程證明:

擬合好壞的評價
通過最小二乘法確定擬合方程后,怎么來評價擬合的好壞呢?
- SST:總體平方和
- SSE:誤差平方和
- SSR: 回歸平方和
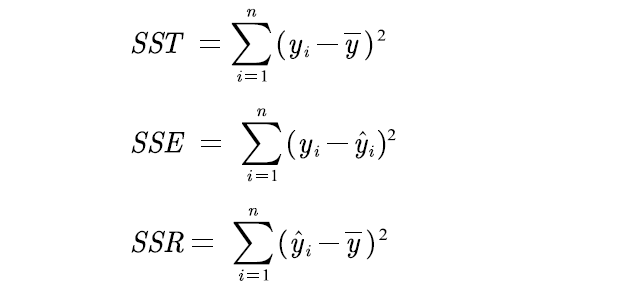
SST = SSE + SSR;
擬合優度:1 - SSE/SST.
R^2越接近1,說明誤差平方和越接近0,誤差越小說明擬合的越好
代碼部分
最小二乘
%% 開始擬合
%行數
n = size(x,1);
%計算擬合參數
k = (n*sum(x.*y) - sum(y)*sum(x))/(n*sum(x.^2)-sum(x)*sum(x));
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x)*sum(x));hold on % 繼續在之前的圖形上來畫圖形
grid on % 顯示網格線
% % 畫出y=kx+b的函數圖像 plot(x,y)
% % 傳統的畫法:模擬生成x和y的序列,比如要畫出[0,5]上的圖形
% xx = 2.5: 0.1 :7 ; % 間隔設置的越小畫出來的圖形越準確
% yy = k * xx + b; % k和b都是已知值
% plot(xx,yy,'-')
匿名函數用法
% 匿名函數的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle為調用匿名函數時使用的名字。
% arglist為匿名函數的輸入參數,可以是一個,也可以是多個,用逗號分隔。
% anonymous_function為匿名函數的表達式。
% 舉個小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函數可用于畫出匿名一元函數的圖形。
% fplot(f,xinterval) 將匿名函數f在指定區間xinterval繪圖。xinterval = [xmin xmax] 表示定義域的范圍% f=@(x) k*x+b;
% fplot(f,[2.5,7]);
擬合優度
%% 求擬合度
y_hat = k*x+b; % y的擬合值
SSR = sum((y_hat-mean(y)).^2) % 回歸平方和
SSE = sum((y_hat-y).^2) % 誤差平方和
SST = sum((y-mean(y)).^2) % 總體平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮點數計算的一個誤差
R_2 = SSR / SST完整代碼
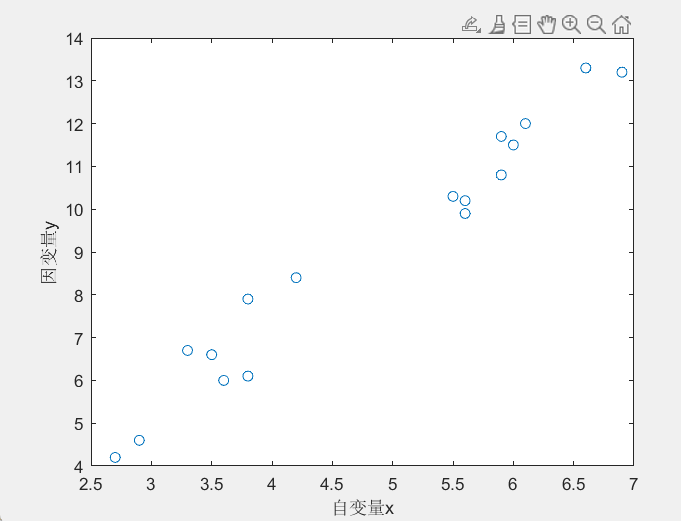
%% 導入數據
load data
%繪制原始散點圖
plot(x,y,'o')
%給x軸與y軸加上標簽
xlabel('自變量x')
ylabel('因變量y')
%% 開始擬合
%行數
n = size(x,1);
%計算擬合參數
k = (n*sum(x.*y) - sum(y)*sum(x))/(n*sum(x.^2)-sum(x)*sum(x));
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x)*sum(x));hold on % 繼續在之前的圖形上來畫圖形
grid on % 顯示網格線
% % 畫出y=kx+b的函數圖像 plot(x,y)
% % 傳統的畫法:模擬生成x和y的序列,比如要畫出[0,5]上的圖形
% xx = 2.5: 0.1 :7 ; % 間隔設置的越小畫出來的圖形越準確
% yy = k * xx + b; % k和b都是已知值
% plot(xx,yy,'-')% 匿名函數的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle為調用匿名函數時使用的名字。
% arglist為匿名函數的輸入參數,可以是一個,也可以是多個,用逗號分隔。
% anonymous_function為匿名函數的表達式。
% 舉個小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函數可用于畫出匿名一元函數的圖形。
% fplot(f,xinterval) 將匿名函數f在指定區間xinterval繪圖。xinterval = [xmin xmax] 表示定義域的范圍% f=@(x) k*x+b;
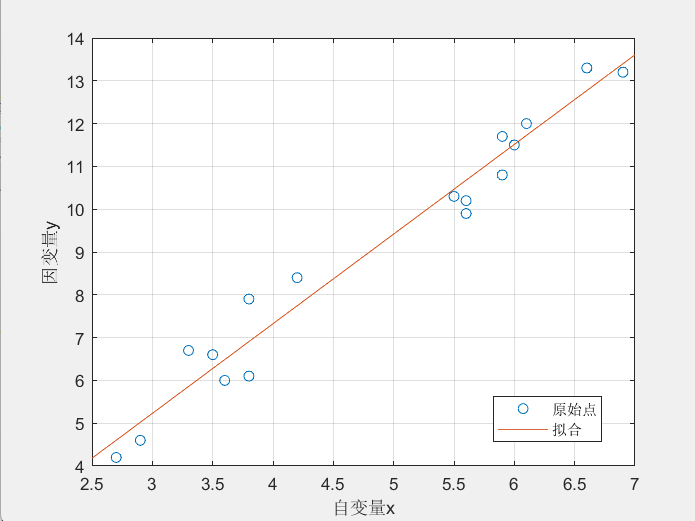
% fplot(f,[2.5,7]);f = @(x) k*x + b;
fplot(f,[2.5,7.0])
legend('原始點','擬合')
%% 求擬合度
y_hat = k*x+b; % y的擬合值
SSR = sum((y_hat-mean(y)).^2) % 回歸平方和
SSE = sum((y_hat-y).^2) % 誤差平方和
SST = sum((y-mean(y)).^2) % 總體平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮點數計算的一個誤差
R_2 = SSR / SST本文由博客一文多發平臺 OpenWrite 發布!





——滑動窗口最大值_困難(中等))


)


】列表詳解)






)
