一、多維數組

（一）數組的定義

數組是由n（n≥1）個相同數據類型的數據元素組成的有限序列，在定義數組時，會為數組分配一個固定大小的內存空間，用來存儲元素，數組在被定義后，其維度不可以被改變。

數組在確定其維度和維界后，元素的個數是固定的，所以不能進行插入和刪除運算。數組中最常見的兩種操作是查找和修改。

（二）二維數組

數組可分為一維數組和多維數組（常見的有二維數組），二維數組可以看作一維數組的一維數組。順序表是一個一維數組，所以它是線性結構，與棧、隊列、串的邏輯結構相同，而多維數組則是典型的非線性結構，也可以說它是嵌套的線性結構。

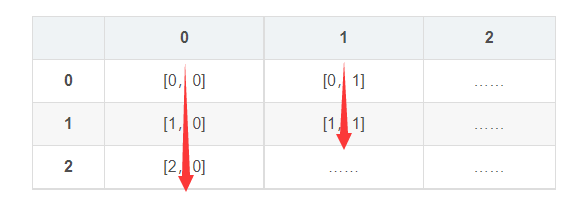
例如，一個二維數組A[3][4]在內存中實際上是一個長度為3的一維數組，每個元素是一個長度為4的一維數組，即對應三行四列，其中元素是從上到下、從左到右依次存儲的，如下：

	0	1	2	3
0	[0，0]	[0，1]	[0，2]	[0，3]
1	[1，0]	[1，1]	[1，2]	[1，3]
2	[2，0]	[2，1]	[2，2]	[2，3]

由于數組中是從下標0開始的，所以一個m行n列的二維數組中，最開始的元素是[0，0]，最后的元素是[m-1，n-1]，上面三行四列的二維數組A[3][4]中的最后一個元素即為[2，3]。

（三）多維數組的存儲

二維數組的存儲較一維數組不一樣，有兩種存儲方式，可分為行優先存儲和列優先存儲，前者是先按每行存儲滿后再繼續下一行，后者相反先按每列存儲滿后再繼續下一列。

例如，定義一個二維數組A[3][3]，在連續的內存空間里，如下：

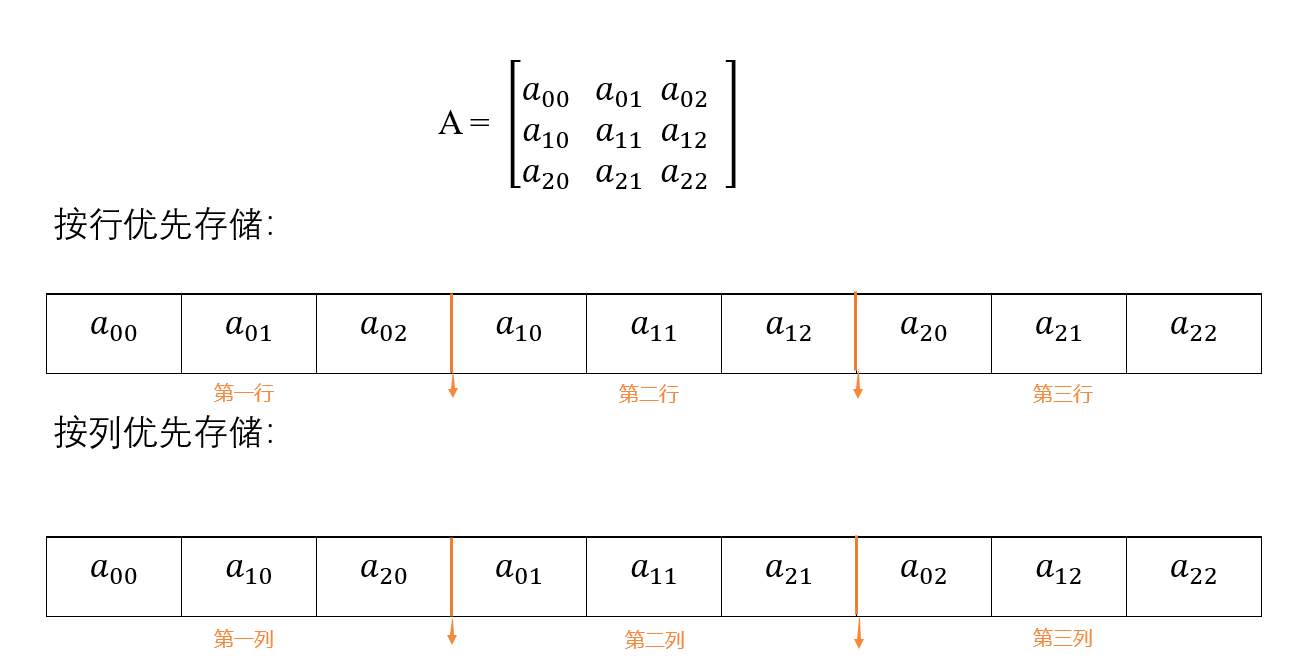
若按照行優先存儲，以A[2][0]為例，在存儲A[2][0]之前，是這樣存儲的：

而按照列優先存儲，以A[1][1]為例，在存儲A[1][1]之前，是這樣存儲的：

（四）多維數組的下標的相關計算

設一個二維數組A[i][j]，其中行下標和列下標的范圍分別為[0，a]和[0，b]，若每個數組元素在內存中占用L個存儲單元，且數組中第一個元素的存儲位置為LOC[c1][c2]，求該二維數組中任意一元素A[i][j]的存儲位置？

1、按行優先存儲
【所求行乘列界限加1，然后加所求列確定位置】
（1）先確定有多少行，加上列數，然后乘以存儲單元，最后加上第一個元素的存儲位置，得：LOC[i][j]=LOC[c1][c2]+[(i-c1)×(b-c2+1)+(j-c2)]×L。
（2）若在編程語言中，由于數組元素下標是從0開始的，該式子改寫為：LOC[i][j]=LOC[0][0]+[i×(b+1)+j]×L。

例、二維數組A[m][n]采用行序為主方式存儲，每個元素占L個存儲單位。元素A[0][0]的存儲地址是b，求元素A[i][j]（0 ≤ i ≤ m-1，0 ≤ j ≤ n-1）的存儲地址。

解析：由于二維數組中行列元素都是從0開始的，即LOC[i][j]=b+[i×(n-1+1)+j]×L=b+[i×n+j]×L。
2、按列優先存儲
【所求列乘行界限加1，然后加所求行確定位置】
（1）先確定有多少列，加上行數，然后乘以存儲單元，最后加上第一個元素的存儲位置，得：LOC[i][j]=LOC[c1][c2]+[(j-c1)×(a-c2+1)+(j-c1)]×L。
（2）若在編程語言中，由于數組元素下標是從0開始的，該式子改寫為： LOC[i][j]=LOC[0][0]+[j×(a+1)+i]×L。

例、設7行6列的數組a以列序為主序順序存儲，基地址為1024，每個元素占2個存儲單元，架設無第0行第0列，求第4行第5列的元素的存儲地址。

解析：由于第一個元素為a[1][1]，所以要減去后再代入計算，即
LOC[4][5]=1024+[(5-1)×(7-1+1)+(4-1)]×2=1024+62=1086。

• 對于一個數組A_n×n（方陣），其元素a_ij按行優先與按列優先存儲時地址之差為(n-1)(i-j)。

二、矩陣

（一）特殊矩陣和稀疏矩陣

相同的元素或零元素在矩陣中的分布存在一定規律的矩陣稱為特殊矩陣，反之則為稀疏矩陣。簡單的來說，特殊矩陣既然特殊，說明其中有很多相同或者有零元素，且存在一定規律在矩陣中分布。

常見的特殊矩陣有對稱矩陣、反對稱矩陣、上/下三角矩陣、對角矩陣等等，例如對角矩陣中，只有對角線上有元素，其余元素均為零：

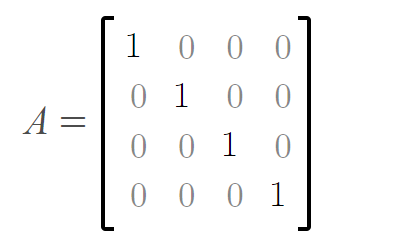
（二）對稱矩陣

若一個方陣滿足A_i×j=A_j×i，則稱為對稱矩陣。由于對稱矩陣中上三角部分和下三角部分的元素對應相同，在存儲對稱矩陣時，為了避免空間的浪費，可以只存儲上或下三角部分的元素，將其存放在一個一維數組中，該數組的大小為1+2+……+n=n(1+n)/2。

（三）對角矩陣

三對角矩陣就是一種對角矩陣，其中非零元素都集中在以主對角線為中心的三條對角線的區域中，其他區域均為零。

（四）稀疏矩陣的壓縮存儲

前面講到，稀疏矩陣中非零元素的分布與特殊矩陣相反，是沒有規律的。稀疏矩陣中大部分元素都為0，且與非零元素的分布一樣，也是沒有規律的。對矩陣壓縮的目的是節省存儲空間。
1、三元組表
為了壓縮存儲稀疏矩陣，在存儲時不僅要存儲矩陣中非零元素的值，同時還要存儲該元素所在的行與列，從而組成一個三元組表（行、列、值），依此減少了存儲空間。由于是將稀疏矩陣中的非零元素以及其對應的行、列號以三元組的形式存儲在一個數組中，所以經過這種壓縮存儲后就無法通過數組的下標直接存取矩陣的元素，失去了隨機存取的特性。另外，稀疏矩陣的三元組表也可以采用十字鏈表法存儲。【稀疏矩陣的兩種存儲結構是三元組表（數組）和十字鏈表】

//以整型int為例，可替換其他類型
typedef struct{int i,j;	//行與列int x;		//值
}Sparsematrix;

例如，一個稀疏矩陣A，進行壓縮存儲：

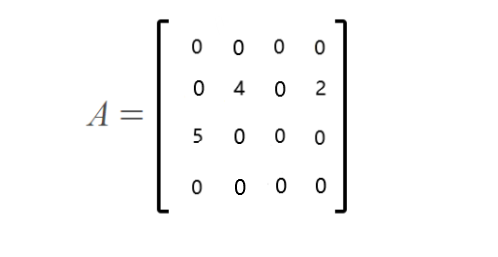
對應的三元組表，如下：

i（行）	j（列）	x（值）
1	1	4
1	3	2
2	0	5

例如，有一個100×90的稀疏矩陣，非0元素有10個，設每個整型數占2字節，則用三元組表示矩陣時，求所需的字節數。

解析：三元組表包括行、列、值，每個整型數占2字節，所以10個非0元素占3×2×10=60字節，另外還有三元組表中行數、列數和總的非零元素個數共6個字節，一共60+6=66字節。

2、十字鏈表
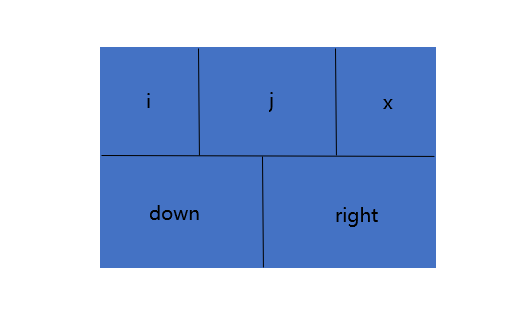
十字鏈表法中，稀疏矩陣的行和列都用一個帶頭結點的鏈表表示，從而對應著五個分量：行、列、數據域、指向下方結點的指針和指向右方結點的指針，其結點的結構如下：

三、廣義表

（一）廣義表的定義

廣義表是線性表的進一步推廣，是由n（n≥0）個數據元素組成的有序序列。線性表中的數據元素只能是單個元素（原子），它是不可分割的，而廣義表中的數據元素既可以是原子，也可以是一個廣義表（包括空表和非空表），廣義表通過圓括號“()”括起來，通過逗號“,”隔開表中的各個數據元素。

一個n維數組可以看成元素是n-1維數組的廣義表，廣義表的元素都是n-1維數組。另外，若廣義表中的所有元素都是原子時，此時的廣義表就是一個線性表。

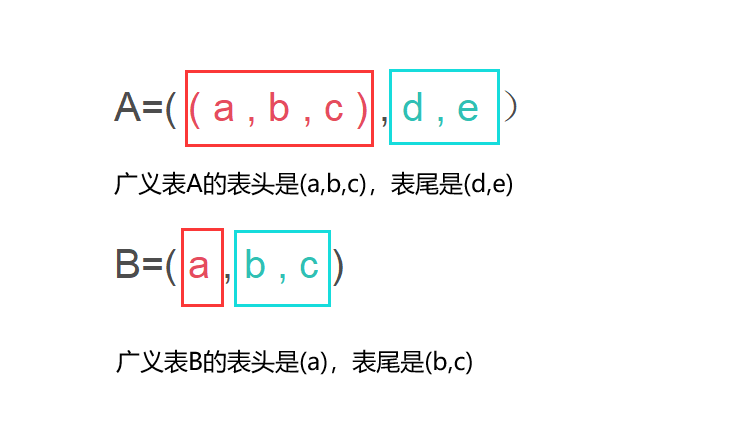
（二）廣義表的表頭和表尾

廣義表是可以遞歸的，一個廣義表也可以是其自身的子表，廣義表中的第一個元素稱為廣義表的表頭，而剩余數據元素組成的表稱為廣義表的表尾，廣義表的表頭和表尾可以看作通過函數Head()和Tail()對廣義表操作。任何一個非空廣義表，表頭可能是單個元素（原子）或廣義表，但表尾只可能是廣義表，其原因是廣義表的取表尾Tail()是非空廣義表除去表頭元素后，剩余元素組成的表，所以不可能是原子。

例如，C=(a,b,c,d,e,f,g)，該廣義表的表頭是(a)，表尾是(b,c,d,e,f,g)；
例如，D=((a,b),((c,d,e),(f,g,h)))，該廣義表的表頭是(a,b)，表尾是((c,d,e),(f,g,h))。

另外，若一個廣義表為空，則為一個空表。例如，E=( )，F=(( ))，廣義表E是一個空表，只有非空廣義表才能取表頭，廣義表F的表頭和表尾都是()。

（三）廣義表的深度和長度

• 廣義表的深度通過括號的層數求得，而長度是廣義表中所含元素的個數。

例如，一個空廣義表G=()，括號層數為1，所以廣義表的深度為1，而由于是空表，所以廣義表的長度為0；
例如，一個廣義表H=((a,b),(c,(d,e)))，括號層數為3，所以廣義表的深度為3，最高層為(c,(d,e))，逗號隔開了原子( c )和廣義表( d,e )，元素個數為2，所以廣義表的長度為2。
例如，一個廣義表I=((),(a),(b,c,(d),((d,f))))，由于括號的最大層數為4，所以廣義表的深度為4，可知廣義表有三個元素，分別是()、(a)、(b,c,(d),((d,f)))，元素個數為3，所以廣義表的長度為3。
例如，設廣義表J=(( ),( ))，對廣義表J，head(J)=( )，Tail(J)=(( ))，括號的最大層數為2，所以廣義表的深度為2，廣義表有兩個元素，分別是()、()，元素個數為2，所以廣義表長度為2。

注：這里的Tail(J)=(( ))，而不是( )。

（四）廣義表表示二叉樹

根據廣義表中“ 數據元素既可以是原子，也可以是一個廣義表（包括空表和非空表) ”這一點可以來表示二叉樹，即通過(根結點，根結點的廣義表)的形式來表示，其中可以嵌套。
例如，下面是一個滿二叉樹：

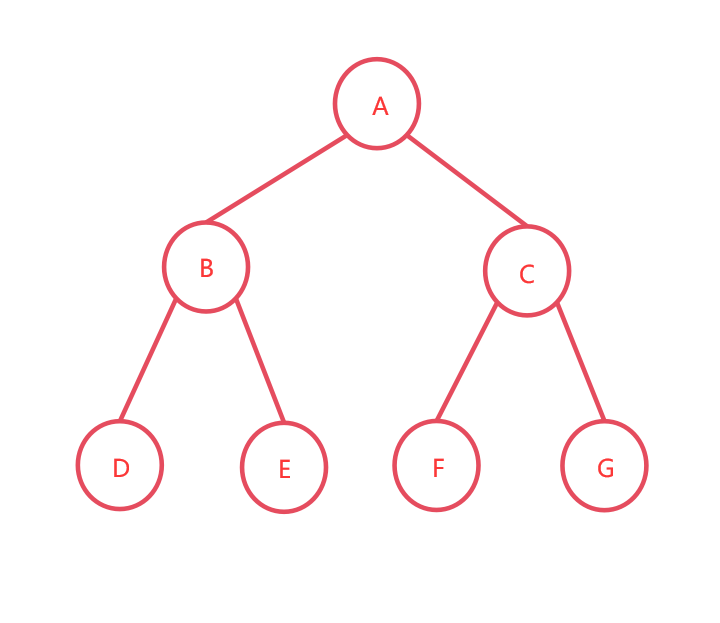
通過廣義表表示該二叉樹：
(A , ( B , ( D , E ) ) , ( C , ( F , G ) ) ) )
這個二叉樹的解釋如下：
根結點是A，它的左孩子是B，B的左孩子是D，B的右孩子是E。
根結點A的右孩子是C，C的左孩子是F，C的右孩子是G。