2017 級考研管理類聯考數學真題解析

一、問題求解（本大題共 5 小題，每小題 3 分，共 45 分）下列每題給出 5 個選項中，只有一個是符合要求的，請在答題卡上將所選擇的字母涂黑。

真題（2017-01）-應用題-

1.某品牌電冰箱連續兩次降價10% 后的售價是降價前的（ ）
A. 80%
B. 81%
C. 82%
D. 83%
E. 85%

真題（2017-02）-應用題

2.張老師到一所中學進行招生咨詢，上午接到了 45 名同學的咨詢，其中的 9 位同學下午又咨詢了張老師，占張老師下午咨詢學生的 10%，一天中向張老師咨詢的學生人數為（ ）
A.81
B.90
C.115
D.126
E.135

真題（2017-03）-數列-等差數列

3.甲、乙、丙三種貨車載重量成等差數列，2 輛甲種車和 1 輛乙種車的滿載量為 95 噸，1輛甲種車和 3 輛丙種車載重量為 150 噸，則用甲、乙、丙各一輛車一次最多運送貨物為（ ）噸
A.125
B.120
C.115
D.110
E.105

真題（2017-04）-算術-絕對值

4.不等式$|x?1|+x\le 2$的解集為（ ）
A.$(?\infty ,1]$
B.$(?\infty ,\frac{3}{2}]$
C.$[1,\frac{3}{2}]$
D.$[1,+\infty )$
E.$[\frac{3}{2},+\infty )$

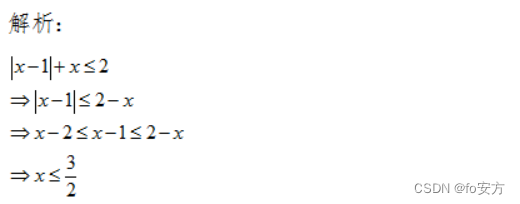
真題（2017-05）-幾何-平面幾何

5.某種機器人可搜索到的區域是半徑為 1 米的圓，若該機器人沿直線行走 10 米，則其搜索出的區域的面積（單位：平方米）為（ ）
A.$10+\frac{\pi }{2}$
B.10+π
C.$20+\frac{\pi }{2}$
D.20+π
E.10π

真題（2017-06）-應用題

6.老師問班上 50 名同學周末復習情況，結果有 20 人復習過數學、30 人復習過語文、6 人復習過英語，且同時復習過數學和語文的有 10 人、同時復習過語文和英語的有 2 人、同時復習過英語和數學的有 3 人。若同時復習過這三門課的人為 0，則沒有復習過這三門課程的學生人數為（ ）
A.7
B.8
C.9
D.10
E.11

真題（2017-07）-實數-整除

7.在 1 到 100 之間，能被 9 整除的整數的平均值是（ ）
A.27
B.36
C.45
D.54
E.63

真題（2017-08）-概率

8.某試卷由 15 道選擇題組成，每道題有 4 個選項，其中只有一項是符合試題要求的，甲有6 道題能確定正確選項，有 5 道能排除 2 個錯誤選項，有 4 道能排除 1 個錯誤選項，若從每題排除后剩余的選項中選一個作為答案，則甲得滿分的概率為（ ）
A.$\frac{1}{2^4}\times \frac{1}{3^5}$
B.$\frac{1}{2^5}\times \frac{1}{3^4}$
C.$\frac{1}{2^5}\times \frac{1}{3^4}$
D. $\frac{1}{2^4}\times (\frac{3}{4}{)}^5$
E.$\frac{1}{2^4}\times (\frac{3}{4}{)}^5$

真題（2017-09）-幾何-平面幾何

9.如圖，在扇形 AOB 中，$\angle AOB=\frac{\pi }{4}，OA=1，$ AC 垂直于OB，則陰影部分的面積為（ ）
A.$\frac{\pi }{8}?\frac{1}{4}$
B.$\frac{\pi }{8}?\frac{1}{8}$
C.$\frac{\pi }{4}?\frac{1}{2}$
D.$\frac{\pi }{4}?\frac{1}{4}$
E.$\frac{\pi }{4}?\frac{1}{8}$

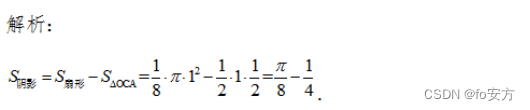
真題（2017-10）-應用題-不定方程

10.某公司用 1 萬元購買了價格分別為 1750 和 950 元的甲、乙兩種辦公設備，則購買的甲、乙辦公設備的件數分別為（ ）
A.3,5
B.5,3
C.4,4
D.2,6
E.6,2

真題（2017-11）-幾何-平面幾何-三角形

11.已知△ABC 和△A’ B’C’ 滿足$|AB|:|A^1{B}^1|=|AC|:|A{C}^1|=2:3，\angle A+\angle A^1=\pi$，則△ABC和△$A^1{B}^1{C}^1$的面積比為（ ）
A.$\sqrt{2}:\sqrt{3}$
B.$\sqrt{3}:\sqrt{5}$
C.2:3
D.2:5
E.4:9

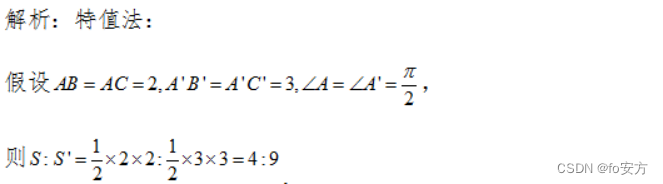
真題（2017-12）-數據分析-

12.甲從 1、2、3 中抽取一個數，記為a ；乙從 1、2、3、4 中抽取一個數，記為b ，規定當a ＞ b 或者a ＋ 1 ＜ b 時甲獲勝，則甲取勝的概率為（ ）
A.$\frac{1}{6}$
B.$\frac{1}{4}$
C.$\frac{1}{3}$
D.$\frac{5}{12}$
E.$\frac{1}{2}$

真題（2017-13）-幾何-立體幾何

13.將長、寬、高分別為 12、9 和 6 的長方體切割成正方體，且切割后無剩余，則能切割成相同正方體的最少個數為（ ）個
A.3
B.6
C.24
D.96
E.648

真題（2017-14）-數據分析-方差

14.甲、乙、丙三人每輪各投籃 10 次，投了三輪.投中數如下表：

	第一輪	第二輪	第三輪
甲	2	5	8
乙	5	2	5
丙	8	4	9

記σ1 ,σ2 ,σ3 分別為甲、乙、丙投中數的方差，則（ ）
A.σ1＞σ2＞σ3
B.σ1＞σ3＞σ2
C.σ2＞σ1＞σ3
D.σ2＞σ3＞σ1
E.σ3＞σ2＞σ1

真題（2017-15）-數據分析-分組分配

15.將 6 人分成 3 組，每組 2 人，則不同的分組方式共有（ ）種
A.12
B.15
C.30
D.45
E.90

二．條件充分性判斷：（第 16-25 小題，每小題 3 分，共 30 分）

要求判斷每題給出的條件（1）和（2）能否充分支持題干所陳述的結論，A、B、C、D、E 五個選項為判斷結果，請選擇一項符合試題要求的判斷，請在答題卡上將所選的字母涂黑。
（A）條件（1）充分，但條件（2）不充分
（B）條件（2）充分，但條件（1）不充分
（C）條件（1）和（2）都不充分，但聯合起來充分
（D）條件（1）充分，條件（2）也充分
（E）條件（1）不充分，條件（2）也不充分，聯合起來仍不充分

真題（2017-16）-D-應用題-工程

16.某人需要處理若干份文件，第一個小時處理了全部文件的 15，第二個小時處理了剩余文件的 14，則此人需要處理的文件共 25 份。
（1）前兩小時處理了 10 份文件
（2）第二小時處理了 5 份文件

真題（2017-17）-A-幾何-解析幾何-圓的方程

17.圓$x^2+y^2?ax?by+c=0$與 x 軸相切，則能確定c 的值。
（1）已知a 的值
（2）已知b 的值

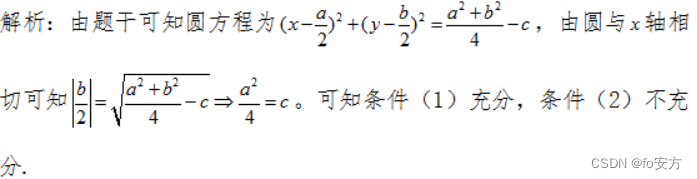
真題（2017-18）-C-應用題-路程

18.某人從 A 地出發，先乘時速為 220 千米的動車，后轉乘時速為 100 千米的汽車到達 B 地，則 A，B 兩地的距離為 960 千米。
（1）乘動車的時間與乘汽車的時間相等
（2）乘動車的時間與乘汽車的時間之和為 6 小時

真題（2017-19）-B-幾何-解析幾何

19.直線$y=ax+b$與拋物線 $y=x^2$ 有兩個交點.

（1） $a^2＞4b$
（2） b ＞0

真題（2017-20）-E-比例應用題-增長率

20.能確定某企業產值的月平均增長率
（1）已知一月份的產值
（2）已知全年的總產值答案

答案應該是E。（否則2017年沒有選E）
首先理解“月平均增長率x”：只與第一個月和最后一個月的產值有關。如：一月a、二、三、四…十一、十二月3a：$a(1+x{)}^{11}=3a$，得$(1+x{)}^{11}=3$，得：$x=\sqrt[11]{3}?1$
∴（2）全年總產值是無關的。更改為“12月的產值”，才選C。

真題（2017-21）-B-幾何-立體幾何

21.如圖，一個鐵球沉入水池中，則能確定鐵球的體積。
（1）已知鐵球露出水面的高度
（2）已知水深及鐵球與水面交線的周長

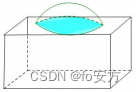
真題（2017-22）-A-代數-數列

22.設a, b 是兩個不相等的實數，則函數$f(x)=x^2+2ax+b$ 的最小值小于零。
（1）1, a, b 成等差數列
（2）1, a, b 成等比數列

真題（2017-23）-C-概率

23.某人參加資格考試，有 A 類和 B 類選擇，A 類的合格標準是抽 3 道題至少會做 2 道，B 類的合格標準是抽 2 道題須都會做，則此人參加 A 類合格的機會大。
（1）此人 A 類題中有 60%會做
（2）此人 B 類題中有 80%會做

真題（2017-24）-C-應用題

24.某機構向 12 位教師征題，共征集到 5 種題型的試題 52 道，則能確定供題教師的人數。
（1）每位供題教師提供題數相同
（2）每位供題教師提供的題型不超過 2 種

真題（2017-25）-A-實數

25.已知a, b, c 為三個實數，則min{$|a?b|,|b?c|,|a?c|$} ≤ 5 .
（1） $|a|\le 5,|b|\le 5,|c|\le 5$
（2） $a+b+c=15$