十大排序

---

排序算法復雜度及穩定性分析

排序方法	最好	平均	最壞	空間復雜的	穩定性	場景
冒泡排序	O(N)(優化情況)	O(N2)	O(N2)	O(1)	穩定	和數據有序無序無關，除非進行優化
插入排序	O(N) (有序情況)	O(N2)	O(N2)	O(1)	穩定	趨于有序時使用，把無序插入有序
選擇排序	O(N2)	O(N2)	O(N2)	O(1)	不穩定	和數據有序無序無關，選一個小的值和前面交換
希爾排序		O(N1.3) 局部結果		O(1)	不穩定	縮小增量分組，最后進行插入排序
堆排序	O(N*log2N)	O(N*log2N)	O(N*log2N)	O(1)	不穩定	和數據有序無序無關,升序建立大根堆，降序小根堆，堆頂元素和最后元素交換
快速排序	O(N*log2N)	O(N*log2N)	O(N2)	O(log2N) ~O（N）	不穩定	數據有序，時間復雜度為O(N2)，O(N*log2N) 最好情況，+優化（三數取中，小區間插入排序）
歸并排序	O(N*log2N)	O(N*log2N)	O(N*log2N)	O（N）	穩定	和數據有序無序無關
計數排序	O(N+K)	O(N+K)	O(N+K)	O(N+K)	穩定	非比較，一組集中在某個范圍內的數據
基數排序	O（NK）	O（NK）	O（NK）	O（N）	穩定	按位分割進行排序，適用于大數據范圍排序，打破了計數排序的限制
桶排序	O(N+K)	O(N2)	O(N+K)	O(N+K)	穩定	劃分多個范圍相同的區間，每個子區間自排序，最后合并

一、 排序的概念

1.排序：

• 一組數據按遞增/遞減排序

2.穩定性：

• 待排序的序列中，存在多個相同的關鍵字，拍完序后，相對次序保持不變，就是穩定的

3.內部排序：

• 數據元素全部放在內存中的排序

4.外部排序：

• 數據元素太多不能同時放在內存中，根據排序過程的要求不能在內外存之間移動數據的排序

二、插入排序

1.直接插入排序

和整理撲克牌類似，將亂序的牌，按值的大小，插入整理好的順序當中

從頭開始，比最后一個小的話依次向前挪，直到大于之前牌時，進行插入

1.如果只有一個值，則這個值有序，所以插入排序， i 從下標1開始，把后面的無序值插入到前面的有序當中

2.j = i-1,是i的前一個數，先用tmp將 i位置的值（要插入的值）先存起來，比較tmp和j位置的值

3.如果tmp的值比 j位置的值小，說明要向前插入到有序的值中，把 j位置的值后移，移動到 j+1的位置，覆蓋掉 i 的值

4.j 下標向前移動一位，再次和 tmp 比較

5.如果tmp的值比 j 位置的值大，說明找到了要插入的位置就在當前j位置之后，把tmp存的值，放到 j+1的位置

6.如果tmp中存的值比有序的值都小，j位置的值依次向后移動一位，j不停減1，直到排到第一位的數移動到第二位，j的下標從0移動到-1，循環結束，最后將tmp中存的值，存放到 j+1的位置，也就是0下標

    public void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];//tmp存儲i的值int j = i - 1;for (; j >= 0; j--) {if (tmp < array[j]) {array[j + 1] = array[j];} else {// array[j+1] = tmp;break;}}array[j + 1] = tmp;}}

插入就是為了維護前面的有序

• 元素越接近有序，直接插入排序算法的時間效率越高

• 時間復雜度O( N ² )

• 空間復雜度O ( 1 )

• 穩定性：穩定

  如果一個排序是穩定的，可以改變實現為不穩定的

  如果是不穩定的排序，則沒有辦法改變

2.希爾排序

希爾排序shellSort 叫縮小增量排序，是對直接插入排序的優化，先分組，對每組插入排序，讓整體逐漸有序

利用了插入排序元素越有序越快的特點

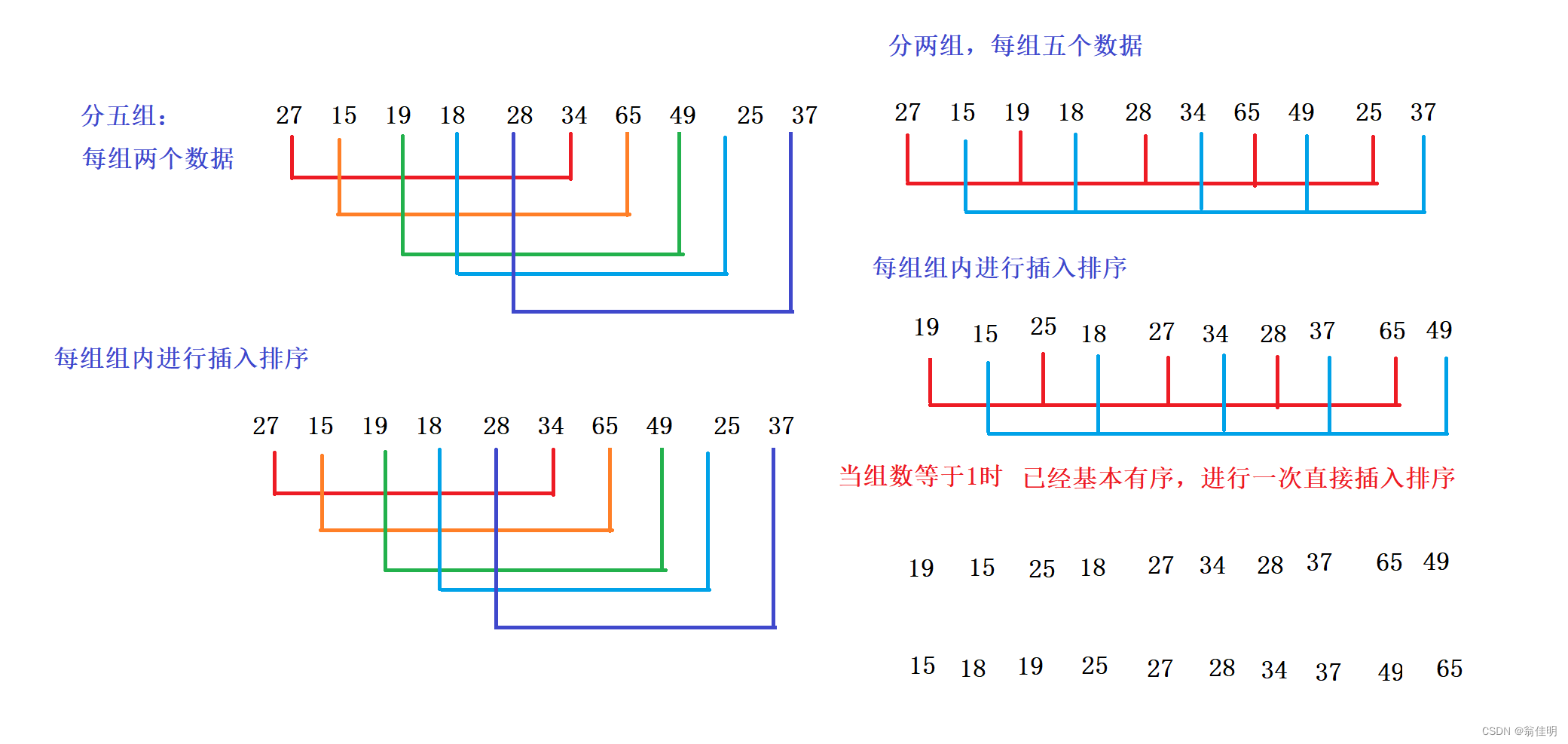
• 先確定一個整數，把待排序數分成多個組，每個組中的數距離相同，
• 對每一組進行排序，然后再次分組排序，減少分組數，組數多，每組數據就少
• 找到分組數=1時，基本有序了，只需要再排一次插入排序即可

一開始組數多，每組數據少，可以保證效率

隨著組數的減少，每組數據變多，數據越來越有序，同樣保證了效率

到達1分組之前，前面的排序都是預排序

    public static void shellSort2(int[] array) {int gap = array.length;while (gap > 1) { //gap>1時縮小增量gap /= 2;//直接在循環內進行最后一次排序shell(array, gap);}}/**** 希爾排序* 時間復雜度O(N^1.3---N^1.5)* @param array*/public static void shellSort1(int[] array) {int gap = array.length;while (gap > 1) { //gap>1時縮小增量shell(array, gap);gap /= 2;//gap==1時不進入循環，再循環為再次排序}shell(array, gap);//組數為1時，進行插入排序}public static void shell(int[] arr, int gap) {//本質上還是插入排序，但是i和j的位置相差為組間距for (int i = gap ; i < arr.length; i++) {int tmp = arr[i];int j = i-gap;for (; j >=0; j -= gap) {if (tmp<arr[j]){arr[j+gap] = arr[j];}else {break;}}arr[j+gap] = tmp;}}

• 時間復雜度：O( N^1.3 ^) ---- O( N^1.5 ^)
• 空間復雜的：O(1)
• 穩定性：不穩定

三、選擇排序

• 在待排序序列中，找到最小值（大）的下標，和排好序的末尾交換，放到待排序列的開頭，直到全部待排序元素排完

1.直接選擇排序

方法一

?

    /*** 選擇排序** @param array*/public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i + 1; j < array.length; j++) {//找最小值if (array[j] < array[minIndex]) {minIndex = j;//只要比minIndex小，放進去}}//循環走完后，minIndex存的就是當前未排序的最小值//將當前i的值和找到的最小值進行交換swap(array,i,minIndex);}}public static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}

1.遍歷數組長度，i從0開始

2.每次循環，都由minIndex = i 來記錄最小值的下標

3.j 從i+1開始遍歷，只要比記錄的最小值小，就讓minIndex記錄。找到未排序中的最小值，進行交換

4.如果遍歷完后，未排序中沒有比minIndex存的值小，i的值就是最小值，i++;

• 效率低, 如果較為有序的序列，在交換時會破壞有序性
• 時間復雜度：O ( N² )
• 空間復雜的：O ( 1 )
• 穩定性：不穩定

方法二

• 上面的方法，只是先選出最小的值，然后和i的位置交換，

• 進行優化：在遍歷時選出最大值和最小值，和收尾進行交換

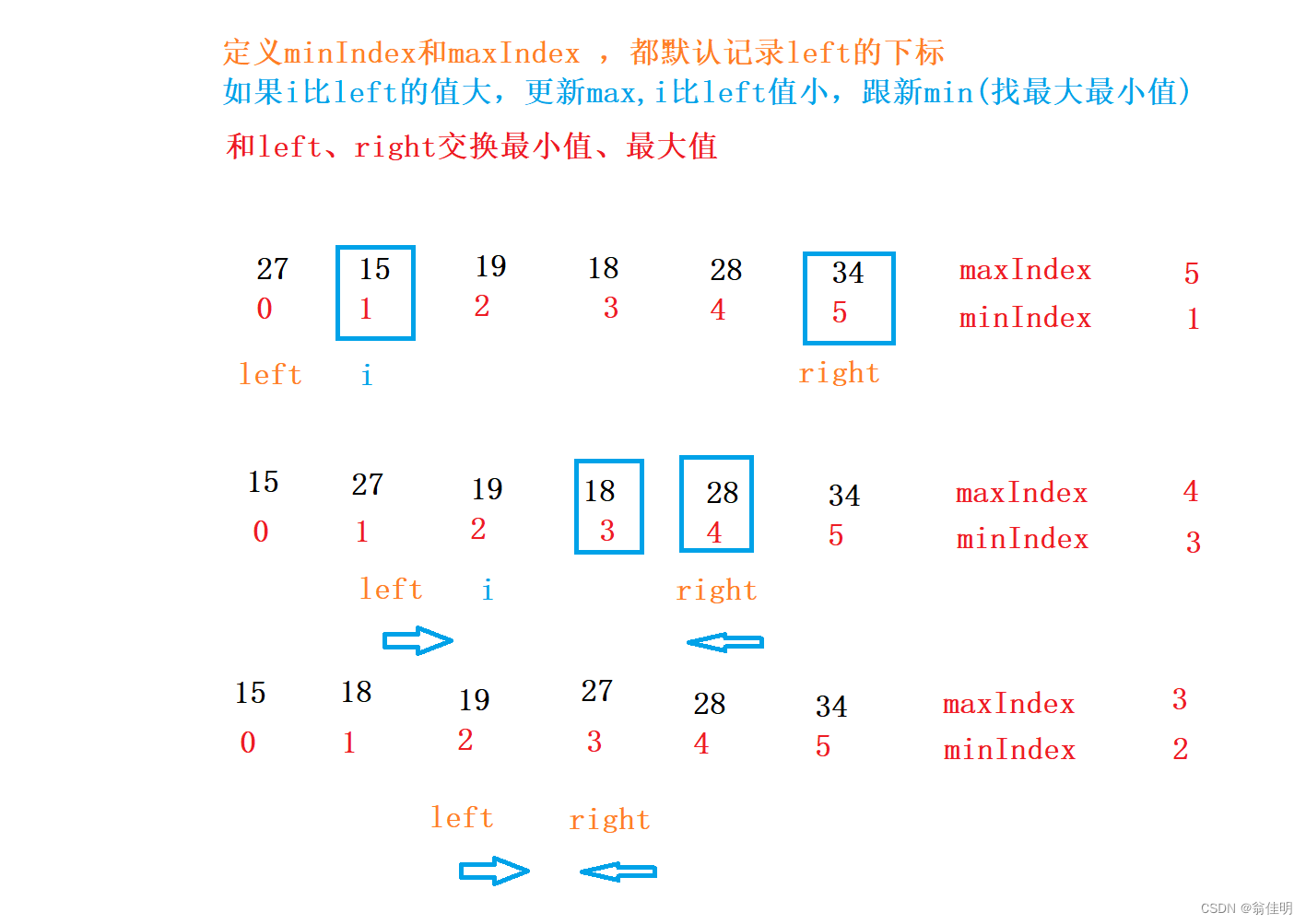
   /*** 選擇排序---選最大值和最小值** @param array*/public static void selectSort2(int[] array) {int left = 0;int right = array.length - 1;while (left < right) {int minIndex = left;int maxIndex = left;//選出最大值和最小值for (int i = left + 1; i <= right; i++) {if (array[i] > array[maxIndex]) {maxIndex = i;}if (array[i] < array[minIndex]) {minIndex = i;}}//用最大值和最小值交換首位swap(array, left, minIndex);//把left和最小值交換//如果left恰好就是最大值，就有可能把最大值換到minIndex的位置if(left == maxIndex){maxIndex = minIndex;//最大值位置不是left了，而是換到了minIndex}swap(array, right, maxIndex);left++;right--;}}

1.在遍歷的過程中，選出最大值的下標和最小值的下標

2.將left和最小值進行交換

3.如果left恰好為最大值，left和最小值交換完成后，最大值就在原來最小值的位置上，

4.maxIndex = minIndex,修正最大值的位置

4.將right和最大值進行交換

直接插入排序和直接排序的區別

• 和插入排序不同的是，插入排序會持續對已排序的數進行比較，把合適的數放在合適的位置
• 直接選擇排序就是不斷找到最小的值，依次放在排好序的末尾，不干預排好的序列

2.堆排序

• 時間復雜度: O( N * log N)
• 空間復雜的：O (1)

• 升序：建大堆

• 降序：建小堆

• 

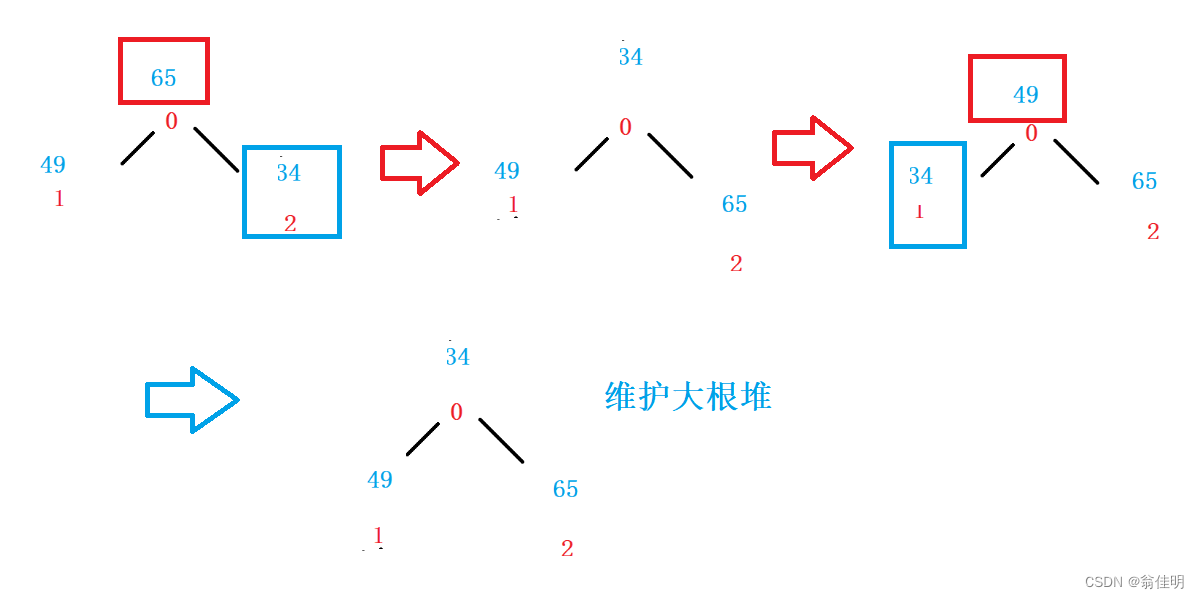
將一組數據從小到大排序 ——> 建立大根堆

為什么不用小根堆：小根堆只能保證，根比左右小，不能保證左右孩子的大小順序，并且要求對數組本身進行排序

• 大根堆，保證堆頂元素是最大值，最大值跟最后一個元素交換，將最大的放在最后，usedSize–；
• 向下調整：調整0下標的樹，維護大根堆，最大值繼續交換到最后一個有效元素的位置
• 從后往前，從大到小依次排列，保證在原來數組本身進行排序

    /*** 堆排序* 時間復雜度: N*logN* 空間復雜的：o(1)** @param array*/public static void heapSort(int[] array) {createBigHeap(array);//創建大根堆int end = array.length-1;while (end>0){swap(array,0,end);//堆頂元素和末尾互換shiftDown(array,0,end);//維護大根堆end--;}}/*** 創建大根堆** @param array*/public static void createBigHeap(int[] array) {//最后一個結點的下標 = array.length - 1//它的父親結點的下標就為array.length - 1 - 1) / 2for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(array, parent, array.length);}}/*** 向下調整** @param array* @param parent* @param len*///向下調整，每棵樹從父結點向下走public static void shiftDown(int[] array, int parent, int len) {int child = parent * 2 + 1;while (child < len) {//child < len:最起碼要有一個左孩子if (child + 1 < len && array[child] < array[child + 1]) {child++;}//child + 1<len:保證一定有右孩子的情況下，和右孩子比較//拿到子節點的最大值if (array[child] > array[parent]) {swap(array, child, parent);parent = child;//交換完成后，讓parent結點等于等于當前child結點child = 2 * parent + 1;//重新求子節點的位置，再次進入循環交換} else {break;//比父結點小，結束循環}}}

• 時間復雜度: O( N * log ₂N)
• 空間復雜的：O (1)
• 穩定性：不穩定

四、交換排序

• 根據序列中兩個記錄鍵值的比較結果來對換這兩個記錄在序列中的位置
• 將鍵值較大的記錄向序列的尾部移動，鍵值較小的記錄向序列的前部移動。

1.冒泡排序

    /*** 冒泡排序* 時間復雜度 n^2* 空間復雜度  1* @param array*/public static void bubbleSort(int[]array){for (int i = 0; i < array.length-1; i++) {//趟數boolean flg =false;for (int j = 0; j < array.length-1-i; j++) {if (array[j]>array[j+1]){swap(array,j,j+1);flg = true;}}if (flg == false){return;}}}

1.遍歷 i 代表交換的趟數，遍歷 j 進行兩兩交換

2.j < array.length-1-i 是對于趟數的優化，每走一趟，交換就少一次

3.boolean flg =false;當兩兩交換時，flg變為true

4.進一步優化：如果遍歷完，沒發生交換，flg還是false,直接返回，排序結束

• 時間復雜度：O ( N² )
• 空間復雜度：O ( 1 )
• 穩定性：穩定

---

2.快速排序

• 時間復雜度：

  最好情況：O (N*log₂N) ：樹的高度為log₂N，每一層都是N

  最壞情況:O (N²)：有序、逆序的情況下,沒有左樹，只有右樹，單分支樹，樹的高度是N,每一層都是N

• 空間復雜的：

  最好情況：O (log₂N)：滿二叉樹（均勻分割待排序的序列，效率最高）樹高為 log₂N

  最壞情況：O（N）:單分支樹,樹高為N

• 穩定性：不穩定

• 二叉樹結構的交換排序方法

• 任取一個待排序元素作為基準值，把序列一分為二，左子序都比基準值小，右子序都比基準值大，左右兩邊再重復進行

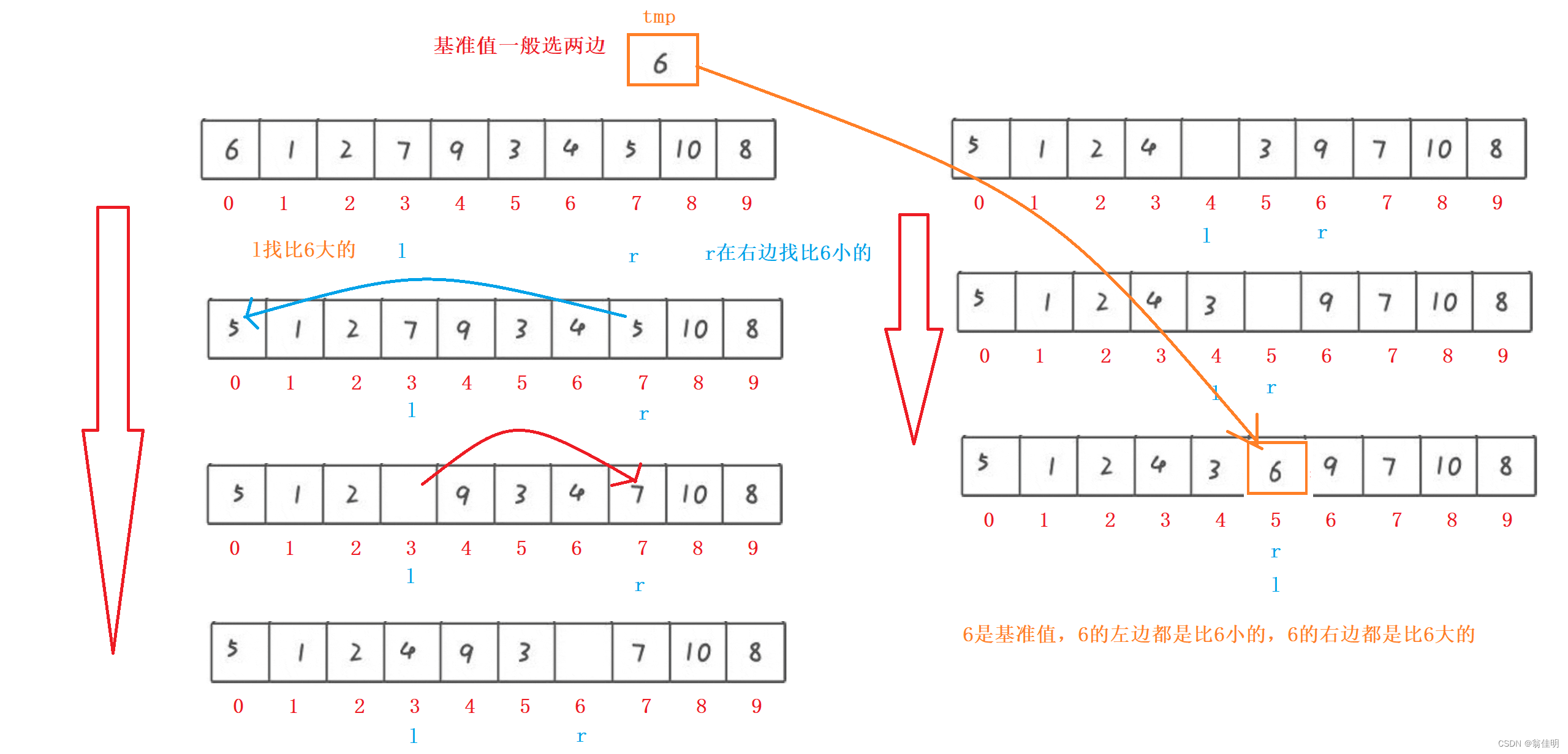
• 左邊找比基準值大的，右邊找比基準值小的

1.挖坑法

• 基準值位置挖一個坑，后面找一個比基準值小的把坑埋上
• 前面找一個比基準值大的，埋后面的坑
• 當l==r時，把基準值填入剩下的坑中

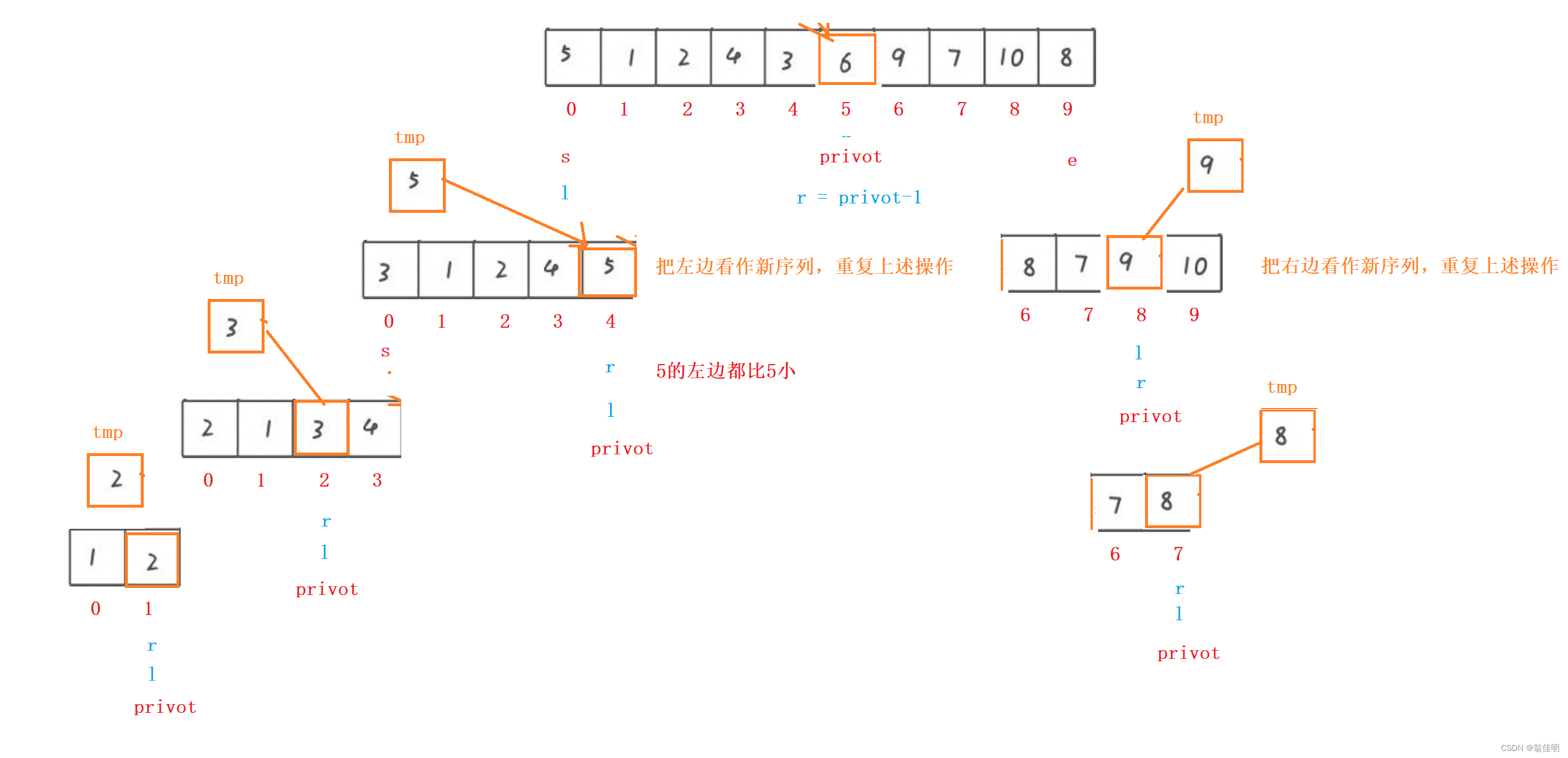
• 左右兩邊重復進行上述步驟，直到排完為止
• 左右兩邊都以同樣的方法進行劃分，運用遞歸來實現

    /*** 快速排序* 時間復雜度:N*log~2~N* 空間復雜度* * @param array*/public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {if (start >= end) {return;//結束條件// start == end，說明只剩一個了，是有序的，返回//start > end ,說明此時的基準值在開頭或者末尾//在開頭：start不變，end=pivot-1,start > end ，end=-1 沒有左樹//在結尾：end不變，start = pivot+1,start > end,超出索引，沒有右樹}//不斷遞歸quickint pivot = partition(array, start, end);// 進行排序，劃分找到pivot//然后遞歸劃分法左邊，遞歸劃分的右邊quick(array, start, pivot - 1);quick(array, pivot + 1, end);}// ---挖坑法  劃分，返回基準值private static int partition(int[] array, int left, int right) {int tmp = array[left];//挖一個坑，取left位置為基準值while (left < right) {//在右邊找一個比基準值小的把坑填上while (left < right && array[right] >= tmp) {//防止越界right--;}array[left] = array[right];//找到比tmp小的數，填坑,//在左邊找一個比tmp大的值，填到右邊的坑while (left < right && array[left] <= tmp) {//防止越界left++;}array[right] = array[left];}//如果相遇了，退出循環array[left] = tmp;//填坑return left;}

• 先劃分序列，遞歸左邊，然后再遞歸右邊

• 遞歸結束條件：

  start == end時，說明只剩一個了，是有序的，返回
  start > end 時 ,說明此時的基準值在開頭或者末尾

  如果基準值在開頭：start不變，end=pivot-1,start > end ，end=-1 沒有左樹
  如果基準值在結尾：end不變，start = pivot+1,start > end,超出索引，沒有右樹

---

2.Hoare法

• 不同的方法，找出基準值，排的序列是不一樣的

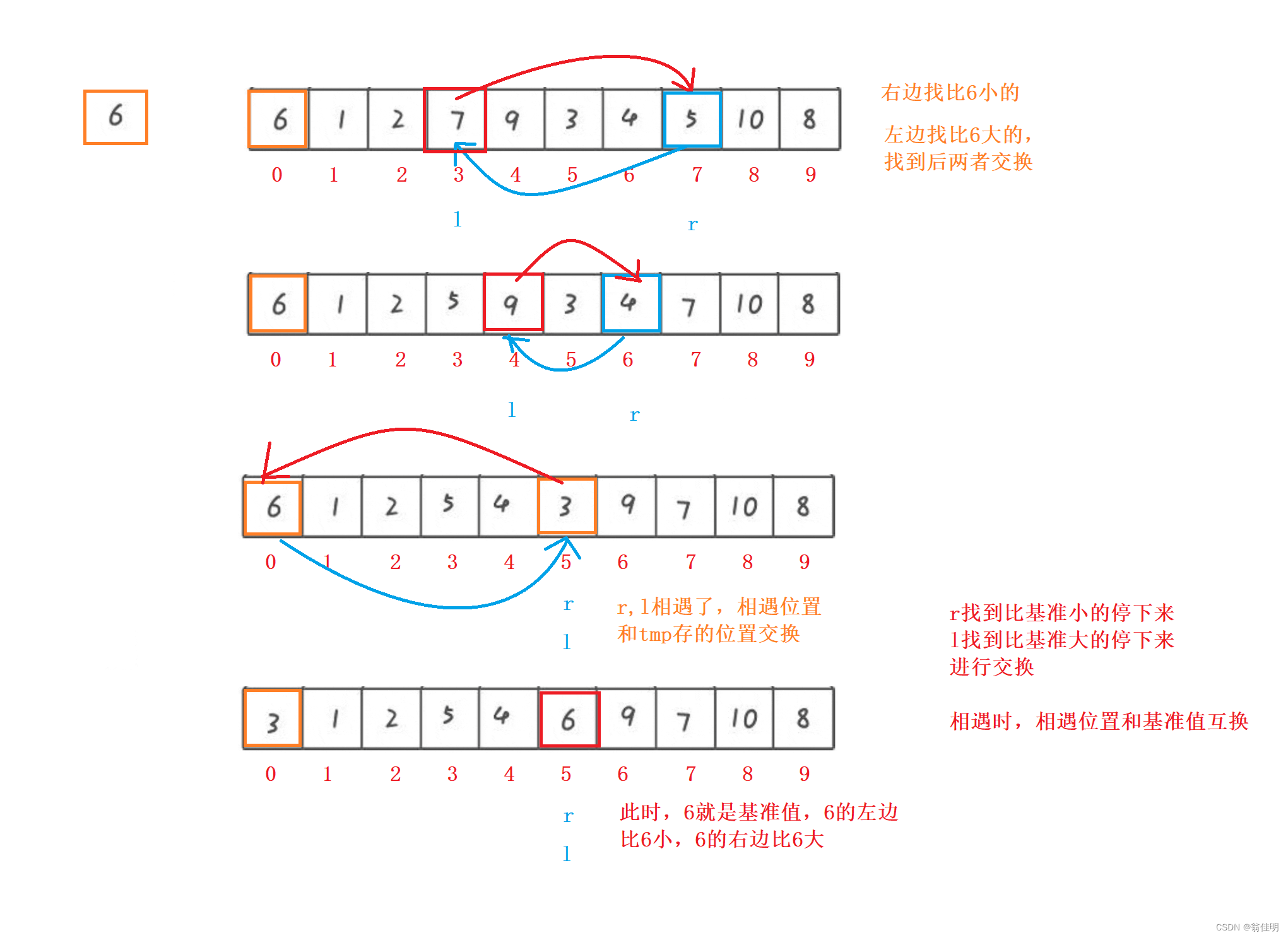
• i記錄基準值一開始在left位置的下標
• r找到比基準值小的停下來，l找到比基準值大的停下來，互相交換
• l和r相遇的時候，把i 記錄基準值的初始下標和相遇位置交換

以左邊為基準，先找右邊再找左邊，相遇的位置就是以右邊為基準的值，要比基準小，才能交換

    /*** Hoare法 劃分排序找基準值* @param array* @param left* @param right* @return*/private static int partition2(int[] array, int left, int right) {int tmp = array[left];int i  = left;//記錄基準值一開始在left位置的下標while (left < right) {while (left < right && array[right] >= tmp) {right--;}while (left < right && array[left] <= tmp) {left++;}swap(array,left,right);}swap(array,i,left);return left;}

3.前后指針法

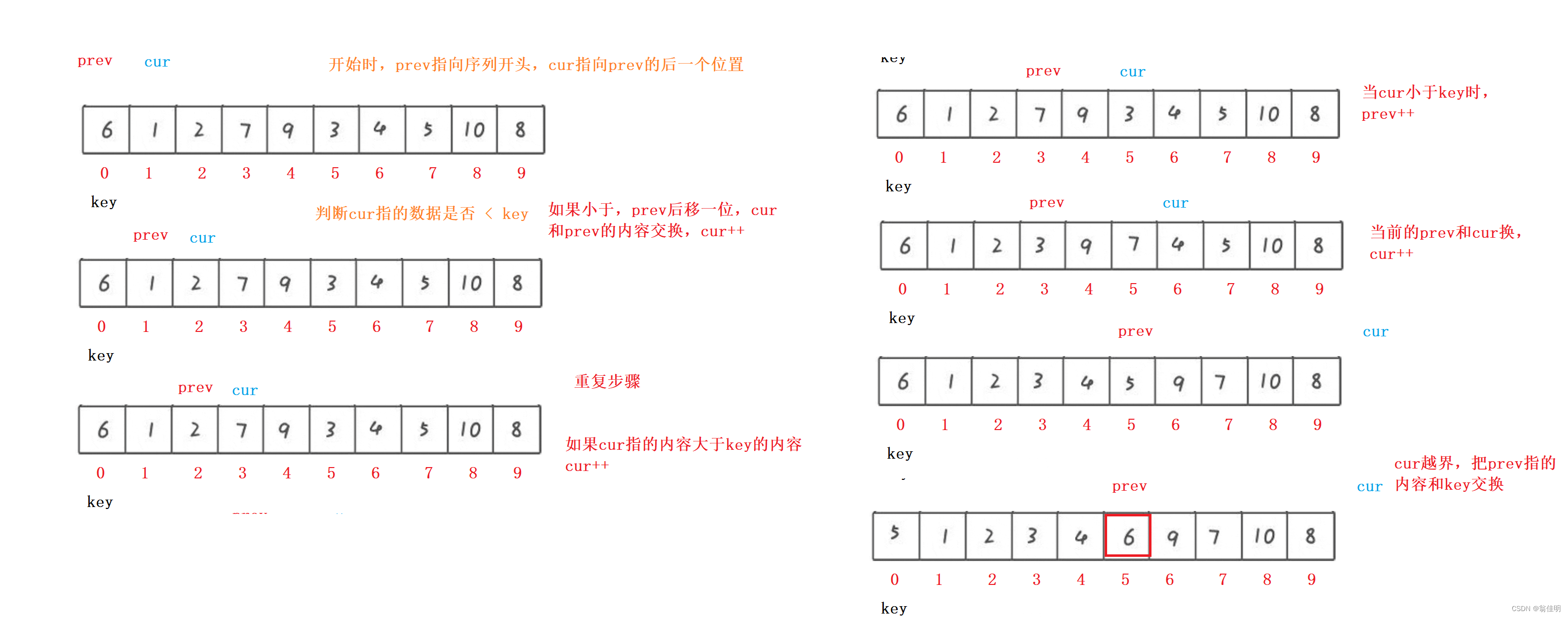
• prev記錄了比key小的最后一個位置
• cur去找比key值小的，找到后，放到prev的下一個位置
• 最后找到基準值，并且基準值的左邊都比它小，右邊都比他大

    /*** 前后指針法，劃分排序找基準值** @param array* @param left* @param right* @return*/private static int partition3(int[] array, int left, int right) {int prev = left; //prev從left位置開始，left為當前的基準值int cur = left + 1;//cur在prev的后一個while (cur <= right) {//遍歷完當前數組段if (array[cur] < array[left] && array[++prev] != array[cur]) {//只要cur指向的值小于left位置的基準值//并且prev++后不等于cur的值swap(array, cur, prev);//將cur和prev位置的值交換//cur++;}//如果cur的值大于基準值,或者prev下一位的值等于cur,cur后移cur++;}//cur越界，循環結束，最后，交換基準值和prev位置的值//prev記錄的就是比基準值小的最后一個數swap(array, prev, left);return prev;//prev為基準值}

4.快速排序的優化

• 時間復雜度：

  最好情況：O (N*log₂N) ：樹的高度為log₂N，每一層都是N

  最壞情況:O (N²)：有序、逆序的情況下,沒有左樹，只有右樹，單分支樹，樹的高度是N,每一層都是N

• 空間復雜的：

  最好情況：O (log₂N)：滿二叉樹（均勻分割待排序的序列，效率最高）樹高為 log₂N

  最壞情況：O（N）:單分支樹,樹高為N

• 穩定性：不穩定

• 快速排序有可能發生棧溢出異常，需要進行優化

• 所以要能均勻分割待排序的序列

遞歸的次數多了，會導致棧溢出，所以優化的方向就是減少遞歸的次數

在最壞情況下，比如順序，基準值都取自左邊，本身沒有左樹

方法一：隨機選取基準值

看人品，有概率

方法二：三數取中法選基準值

三數：第一個數、中間的數、最后一個數 ，在這三個數中，選出中等值

有可能會變成二分查找 ，避免了出現最壞情況，從中值來比較排序，左右樹都有

    public static void quickSort(int[] array) {quick2(array, 0, array.length - 1);}private static void quick2(int[] array, int start, int end) {if (start >= end) {return;//結束條件}//三數取中法int index = midThree(array, start, end);//選出的數和開頭交換swap(array,index,start);int pivot = partition(array, start, end);// 進行排序，劃分找到pivot//然后遞歸劃分法左邊，遞歸劃分的右邊quick2(array, start, pivot - 1);quick2(array, pivot + 1, end);}/*** 三數取中* @param array* @param left* @param right* @return*/private static int midThree(int[] array, int left, int right) {int mid = (left + right) / 2;if (array[left] < array[right]) {if (array[mid] < array[left]) {return left;} else if (array[mid] > array[right]) {return right;} else {return mid;}} else {if (array[mid] < array[right]) {return right;} else if (array[mid] > array[left]) {return left;} else {return mid;}}}

方法三：遞歸到最小區間時、用插入排序

進一步優化：減少遞歸的次數：

• 把快排的遞歸想象成二叉樹，最后兩層包含了大部分數，我們要減少這部分的遞歸

• 前幾次的找基準值排序，導致后面幾層趨于有序，用直接插入法來排序，進一步提高效率，有點像希爾排序

如果樹的高度為h,最后一層就有 2 ^h-1 個結點 ，后兩層占了絕大部分

設置條件：end-start+1 就是當前待排序列的長度，如果小于等于某個較小的值，直接采用插入排序來排剩下的

 private static void quick2(int[] array, int start, int end) {if (start >= end) {return;//結束條件}//優化----減少遞歸的次數if(end-start+1<=20){//如果當前數列的長度，小于=15的時候，// 用插入排序,然后退出insertSortQ(array,start,end);return;}//三數取中法int index = midThree(array, start, end);swap(array,index,start);int pivot = partition(array, start, end);// 進行排序，劃分找到pivot//然后遞歸劃分法左邊，遞歸劃分的右邊quick2(array, start, pivot - 1);quick2(array, pivot + 1, end);}/*** 插入排序---來排剩下的待排部分，給定需要的區間*/private static void insertSortQ(int[] array,int left,int right) {for (int i = left+1; i <= right; i++) {int tmp = array[i];int j = i - 1;for (; j >= left; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}

5.快速排序非遞歸實現

• 1.通過使用棧來實現
• 2.每次找到基準值后，把兩段序列的開頭和末尾壓棧
• 3.從棧頂取出兩個元素作為新序列的首尾，再次找基準值
• 4.找到基準值后，如果右邊有一個元素，不進棧，有兩個元素的才能進棧
• 5.pivot< end-1:證明右邊有兩個元素，pivot>s+1：證明左邊有兩個元素
• 6.棧為空的時候，排完元素

      /*** 非遞歸實現快速排序** @param array*/public static void quickSortNonRecursive(int[] array) {Deque<Integer> stack = new LinkedList<>();//利用棧來實現int left = 0;int right = array.length - 1;//先找到基準值int pivot = partition(array, left, right);//左邊有兩個元素時，根據基準值進棧if (pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//有邊有兩個元素時，根據基準值進棧if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}//棧不為空的時候，取兩個棧頂元素做為區間//再次進棧出棧while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition(array, left, right);//左邊有兩個元素時，根據基準值進棧if (pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}//有邊有兩個元素時，根據基準值進棧if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}}

五、歸并排序

---

• 時間復雜度：O ( N * log_zN ) 每一層都是N,有log₂N層
• 空間復雜度：O（N），每個區間都會申請內存，最后申請的數組大小和array大小相同
• 穩定性：穩定

目前為止，穩定的排序有：插入、冒泡、歸并

• 歸并排序（MERGE-SORT）是建立在歸并操作上的一種有效的排序算法，采用了分治法

• 將待排序列分解，先使每個子序列有序，再使子序列段間有序
• 將已有序的子序列合并，得到完全有序的序列
• 若將兩個有序表合并成一個有序表，稱為二路歸并

1.遞歸實現

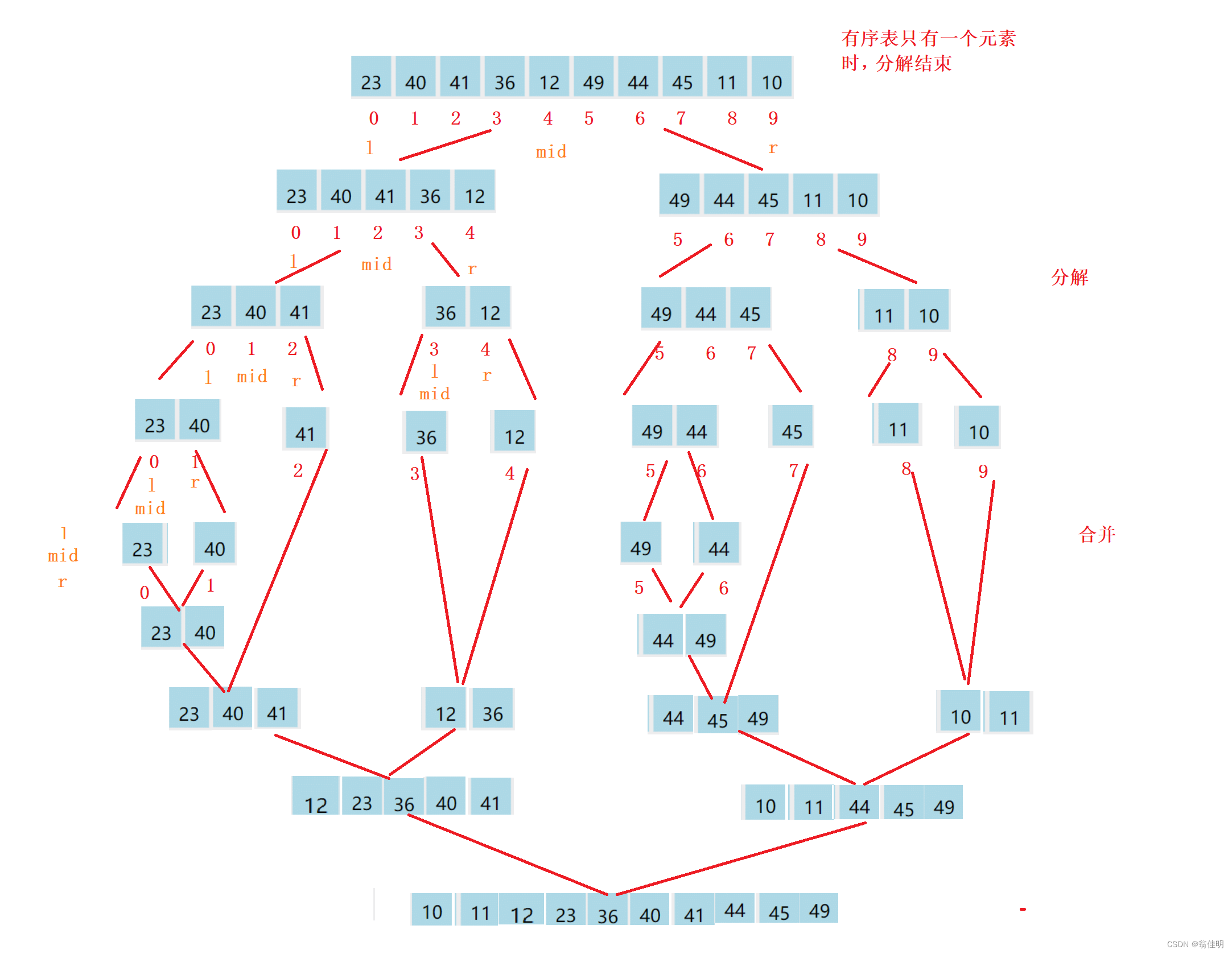
• 1.確定遞歸的結束條件，求出中間數mid,
• 2.進行分解，根據mid來確定遞歸的區間大小
• 3.遞歸分解完左邊，然后遞歸分解右邊
• 4.左右分解完成后，進行合并
• 5.申請新數組進行合并，比較兩個數組段，記得查漏補缺
• 6.和并的時候要對齊下標，每個tmp的下標要找到array中對應的下標

/*** 歸并排序* @param array*/public static void mergeSort(int[] array) {mergeSortFunc(array,0,array.length-1);}private static void mergeSortFunc(int[] array, int left, int right) {//結束條件if (left >= right) {return;}//進行分解int mid = (left + right) / 2;mergeSortFunc(array, left, mid);mergeSortFunc(array, mid + 1, right);//左右分解完成后，進行合并merge(array, left, right, mid);}//進行合并private static void merge(int[] array, int start, int end, int mid) {int s1 = start;int s2 = mid + 1;int[] tmp = new int[end - start + 1];int k = 0;//k為tmp數組的下標while (s1 <= mid && s2 <= end) {//兩個數組中都有數據//進行比較，放到新申請的數組if (array[s1] <= array[s2]) {tmp[k++] = array[s1++];} else {tmp[k++] = array[s2++];}}//因為有&&條件，數組不一定走完while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= end) {tmp[k++] = array[s2++];}//此時，將排好的tmp數組的數組，拷貝到arrayfor (int i = 0; i < tmp.length; i++) {array[i+start] = tmp[i];//對齊下標}}

2.非遞歸實現

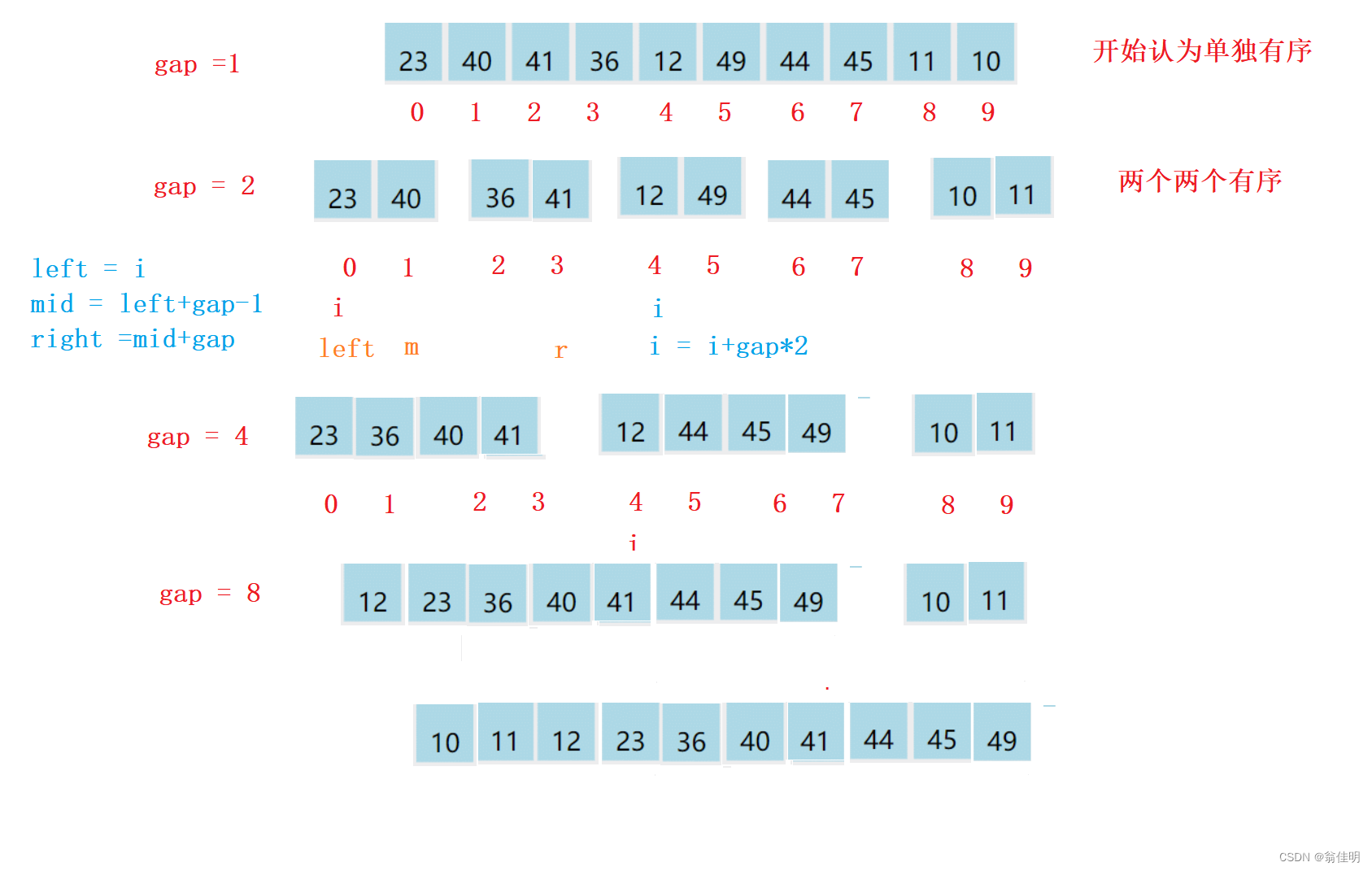
• 1.從1開始分組，先保證每個數都是獨立有序的
• 2.進行循環，i下標從0開始，每次跳轉組數的兩倍
• 3.根據left = i,求出mid和right
• 4.要避免mid和right越界
• 5.分組進行合并
• 6.二倍數擴大組數

/**** 歸并排序，非遞歸實現* @param array*/public static void mergeSort2(int[] array) {int gap = 1;while (gap < array.length) {//i += gap * 2 i每次跳到下一組for (int i = 0; i < array.length; i += gap * 2) {int left = i;//要避免mid和right越界int mid = left + gap - 1;if(mid>=array.length){mid = array.length-1;//修正越界的情況}int right = mid + gap;if (right>=array.length){//修正越界的情況right = array.length-1;}merge(array,left,right,mid);//進行合并}gap *=2;//2倍數擴大組數}}//進行合并private static void merge(int[] array, int start, int end, int mid) {int s1 = start;int s2 = mid + 1;int[] tmp = new int[end - start + 1];int k = 0;//k為tmp數組的下標while (s1 <= mid && s2 <= end) {//兩個數組中都有數據//進行比較，放到新申請的數組if (array[s1] <= array[s2]) {tmp[k++] = array[s1++];} else {tmp[k++] = array[s2++];}}//因為有&&條件，數組不一定走完while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= end) {tmp[k++] = array[s2++];}//此時，將排好的tmp數組的數組，拷貝到arrayfor (int i = 0; i < tmp.length; i++) {array[i + start] = tmp[i];//對齊下標}}

3.海量數據的排序問題

外部排序：排序過程需要在磁盤等外部存儲進行的排序

前提：內存只有 1G，需要排序的數據有 100G

因為內存中因為無法把所有數據全部放下，所以需要外部排序，而歸并排序是最常用的外部排序

1. 先把文件切分成 200 份，每個 512 M
2. 分別對 512 M 排序，因為內存已經可以放的下，所以任意排序方式都可以
3. 進行 2路歸并，同時對 200 份有序文件做歸并過程，最終結果就有序了

六、計數排序

• 時間復雜度：
• 空間復雜度：
• 穩定性：穩定

概念：

• 非基于比較的排序

• 計數排序又稱為鴿巢原理，是對哈希直接定址法的變形應用

  1.統計相同元素出現的個數

  2.根據統計的結果將序列回收到原來的序列中

• 計數排序使用的場景：給出指定范圍內的數據進行排序

• 使用場景：一組集中在某個范圍內的數據

寫法一：

• 通過遍歷計數數組，循環輸出計數數組存的次數

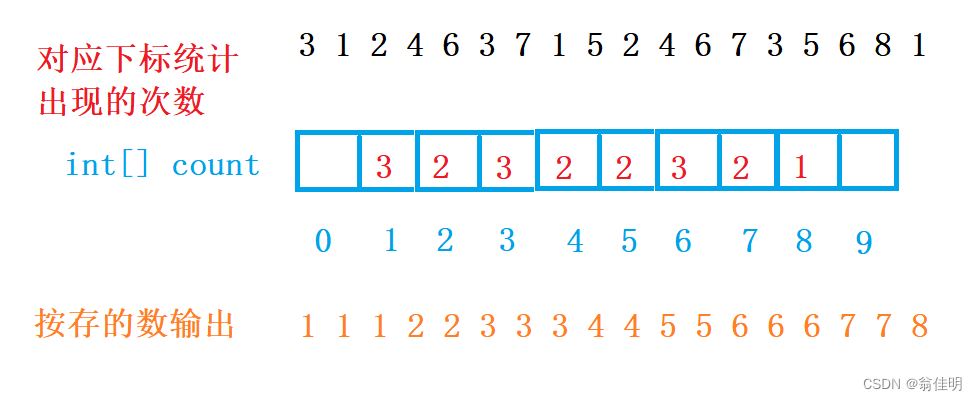
• 1.遍歷數組找到最小值最大值
• 2.根據最大最小值，申請一個計數數組
• 3.遍歷待排數組進行計數
• 4.遍歷計數數組進行輸出

 /*** 計數排序*無法保證穩定* @param array*/public static void countSort2(int[] array) {//1.遍歷數組找到最大值和最小值int MAX = array[0];int MIN = array[0];for (int i = 1; i < array.length; i++) {if (array[i] > MAX) {MAX = array[i];}if (array[i] < MIN) {MIN = array[i];}}//2.根據最大最小值，申請一個計數數組int len = MAX - MIN + 1;//長度int[] count = new int[len];//3. 遍歷待排數組進行計數for (int i = 0; i < array.length; i++) {count[array[i] - MIN]++;}//4.遍歷計數數組進行輸出int index = 0;//array數組新的下標for (int i = 0; i < count.length; i++) {while (count[i] > 0) {array[index] = i + MIN;//+最小值，求出真正的數count[i]--;index++;}}}

寫法二：

• 寫定數組的大小，用臨時數組存儲結構
• 計算每個元素在排序后的數組中的最終位置
• 根據計數數組將元素放到臨時數組b中，實現排序
• 從后往前，根據原來數組的內容，在計數數組中找到要填寫在b數組中的位置，
• 計數數組記錄的不再是數字出現是次數，而是應該在數組中存放的位置下標

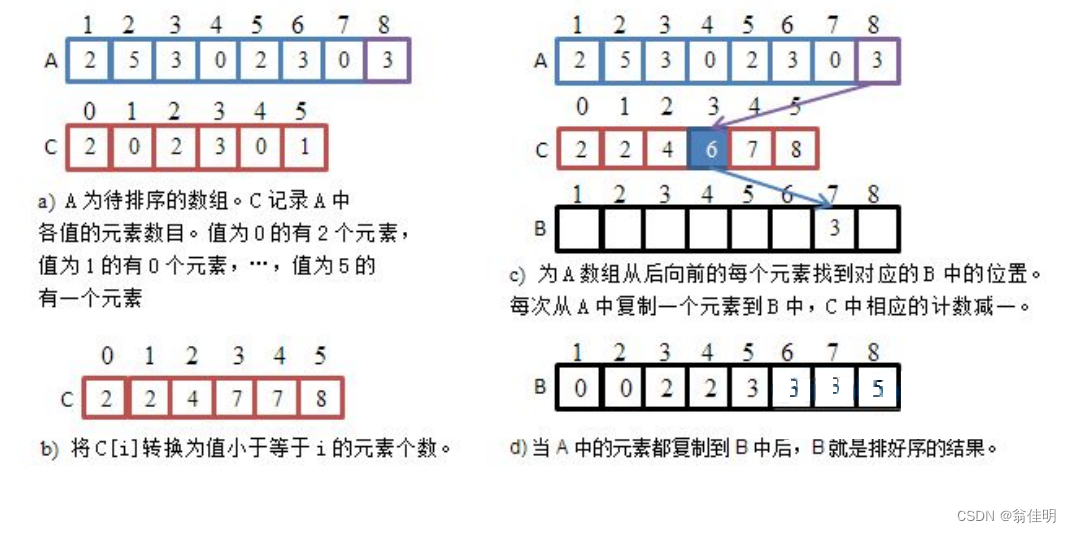
 /*** 計數排序*穩定* @param array*/public static void countSort(int[] array) {int len = array.length;final int MAX = 256;//常量確定數組大小int[] c = new int[MAX];//計數數組int[] b = new int[MAX];//臨時數組，存放結果//統計每個元素的出現次，進行計數for (int i = 0; i < len; i++) {c[array[i]]++;// 將a[i]作為索引，對應計數數組c中的位置加1}// 計算每個元素在排序后的數組中的最終位置for (int i = 1; i < MAX; i++) {c[i] += c[i - 1];// 計數數組中每個元素的值等于它前面所有元素的值之和}// 根據計數數組將元素放到臨時數組b中，實現排序for (int i = len - 1; i >= 0; i--) {b[c[array[i]] - 1] = array[i];// 將a[i]放入臨時數組b中的正確位置c[array[i]]--;// 對應計數數組c中的位置減1，確保相同元素能夠放在正確的位置}// 將臨時數組b中的元素復制回原數組a，完成排序for (int i = 0; i < len; i++) {array[i] = b[i];}}

七、桶排序

概念

劃分多個范圍相同的區間，每個子區間自排序，最后合并

• 桶排序是計數排序的擴展版本，計數排序：每個桶只存儲單一鍵值

• 桶排序： 每個桶存儲一定范圍的數值，確定桶的個數和范圍

• 將待排序數組中的元素映射到各個對應的桶中，對每個桶進行排序

• 最后將非空桶中的元素逐個放入原序列中

代碼

    public static void bucketSort(int[] array){// 計算最大值與最小值int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int i = 0; i < array.length; i++){max = Math.max(max, array[i]);min = Math.min(min, array[i]);}// 計算桶的數量int bucketNum = (max - min) / array.length + 1;ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());}// 將每個元素放入桶for(int i = 0; i < array.length; i++){int num = (array[i] - min) / (array.length);bucketArr.get(num).add(array[i]);}// 對每個桶進行排序for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));}// 將桶中的元素賦值到原序列int index = 0;for(int i = 0; i < bucketArr.size(); i++){for(int j = 0; j < bucketArr.get(i).size(); j++){array[index++] = bucketArr.get(i).get(j);}}}

八、基數排序

概念

• 基數排序是一種非比較型整數排序算法

• 將整數按位數切割成不同的數字，然后按每個位數分別比較

• 使用場景：按位分割進行排序，適用于大數據范圍排序，打破了計數排序的限制

• 穩定性：穩定

• 按位分割技巧：arr[i] / digit % 10，其中digit為10^n。

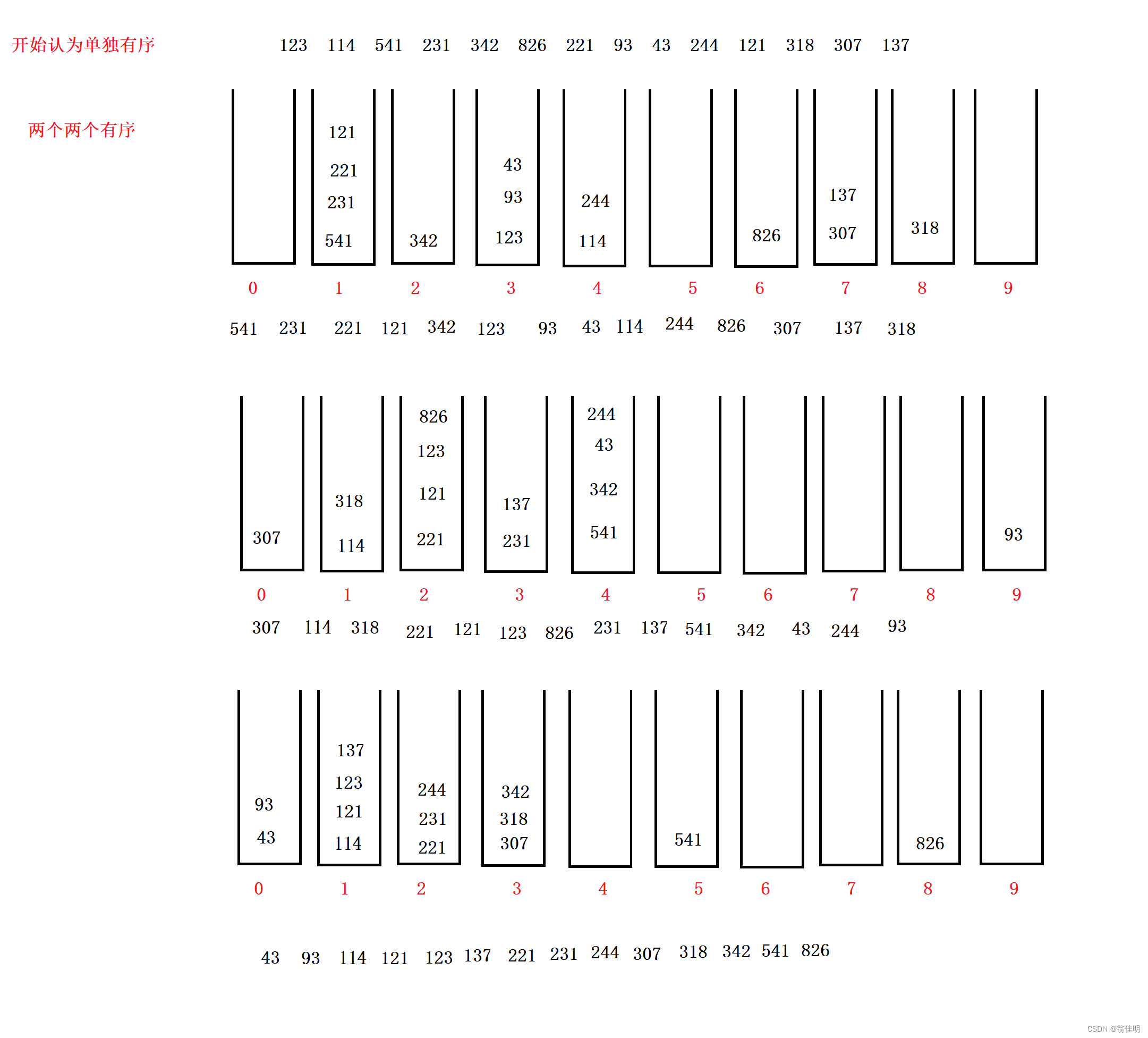
1.LSD排序法（最低位優先法）

• 從最低位向最高位依次按位進行計數排序。

• 進出的次數和最大值的位數有關

• 桶可以用隊列來表示

• 數組的每個元素都是隊列

• 1.先遍歷找到最大值
• 2.求出最高位

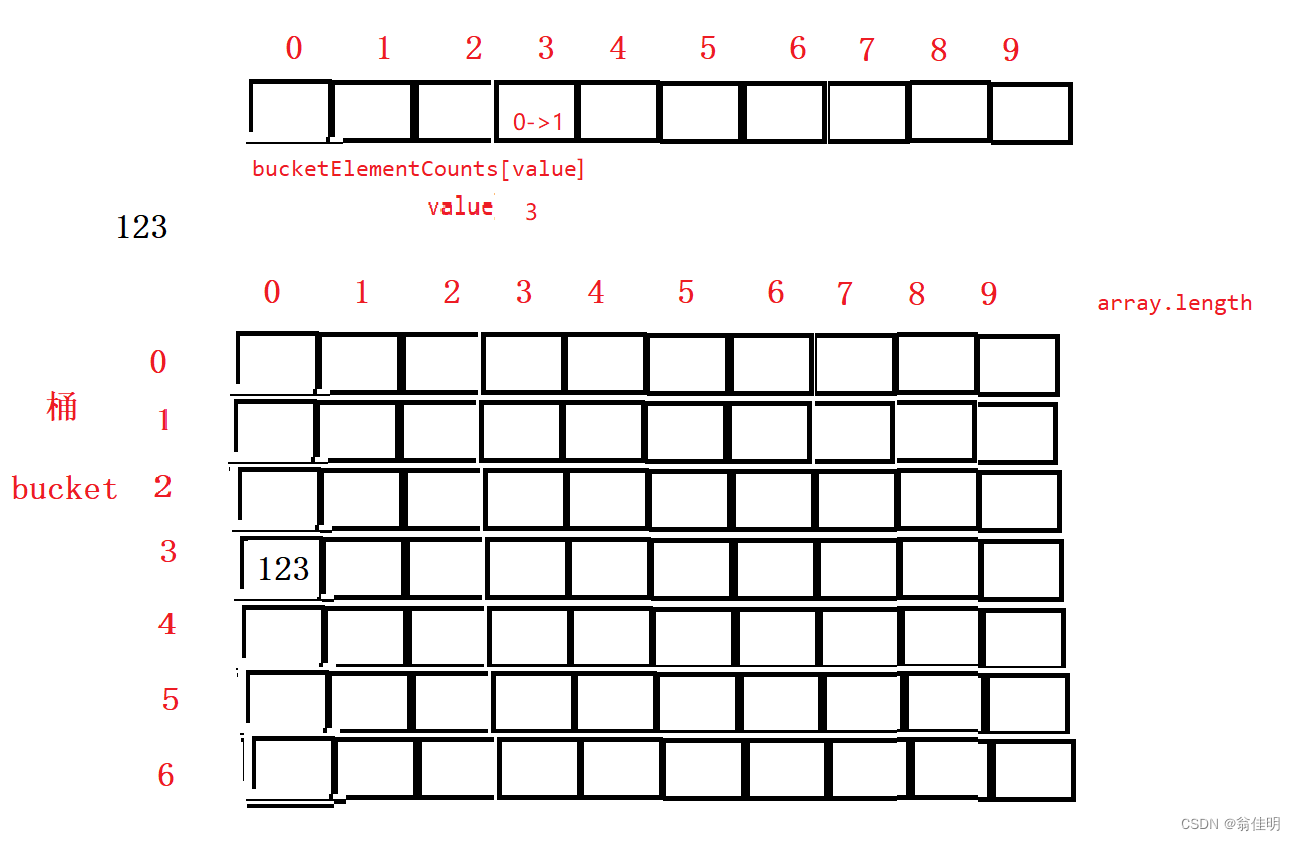
    public static void radixSortR(int[] array) {//10進制數，有10個桶，每個桶最多存array.length個數int[][] bucket = new int[10][array.length];//桶里面要存的具體數值int[] bucketElementCounts = new int[10];//用來計算，統計每個桶所存的元素的個數，每個桶對應一個元素//1.求出最大數int MAX = array[0];for (int i = 1; i < array.length; i++) {if (array[i] > MAX) {MAX = array[i];}}//求最大值的位數，先變成字符串，求字符串長度int MAXCount = (MAX + "").length();//最大位數的個數，進行幾次計數排序for (int i = 0; i < MAXCount; i++) {//i代表第幾次排序//放進桶中for (int k = 0; k < array.length; k++) {//k相當于遍歷待排數值//array[k] /(int) Math.pow(10, i)%10 求出每次要比較位的數//求的是個位，并且是對應趟數的個位int value = (array[k] / (int) Math.pow(10, i)) % 10;//根據求出的位數，找到對應桶，放到對應桶的位置bucket[value][bucketElementCounts[value]] = array[k];//不管value 為多少，bucketElementCounts[value]的值都為0//相當于存到對應桶的0位bucket[value][0]bucketElementCounts[value]++; //從0->1//對應桶的技術數組開始計數}//取出每個桶中的元素，賦值給數組int index = 0;//array新的下標for (int k = 0; k < bucketElementCounts.length; k++) {//遍歷每個桶if (bucketElementCounts[k] != 0) {//桶里有元素for (int j = 0; j < bucketElementCounts[k]; j++) {//比那里每個桶的元素array[index] = bucket[k][j];index++;}}bucketElementCounts[k] =0;//每個桶遍歷完后，清空每個桶的元素；}}}

2.MSD排序法（最高位優先法）

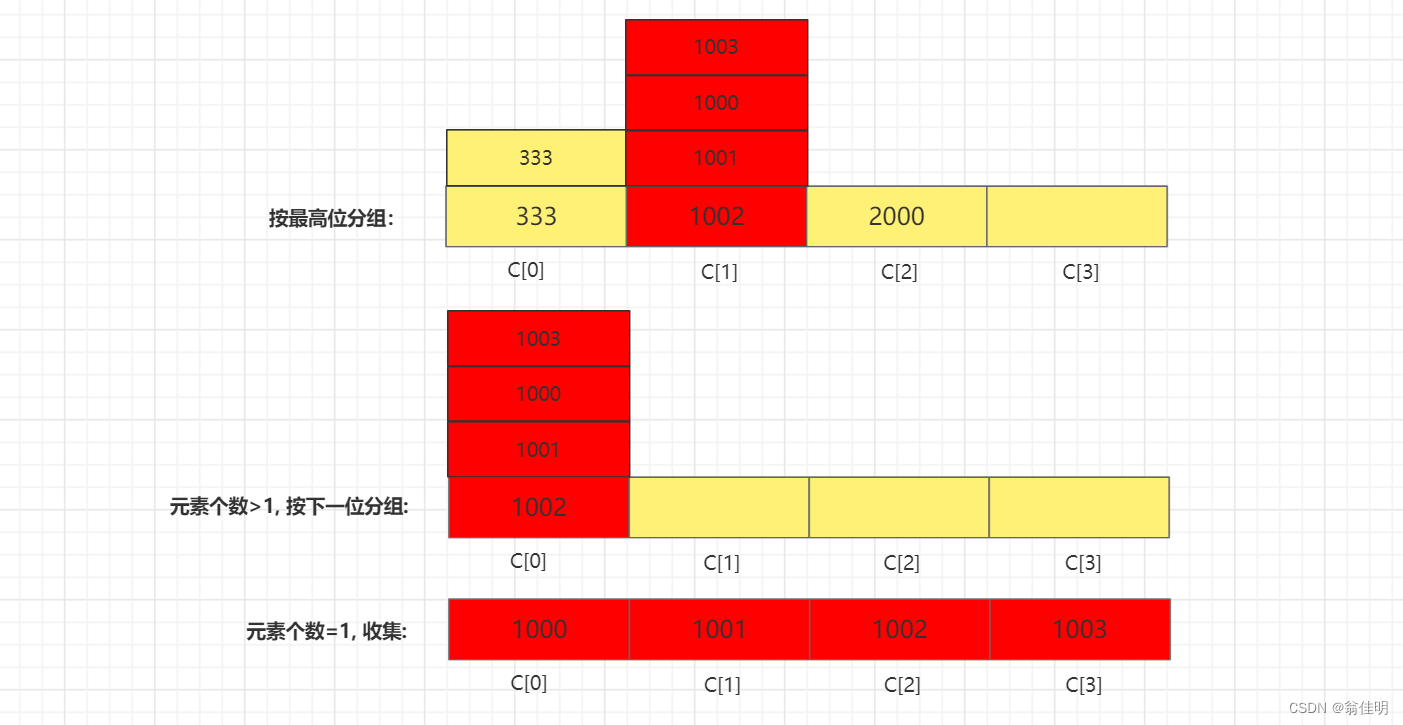
• 從最高位向最低位依次按位進行排序。
• 按位遞歸分組收集
• 1.查詢最大值，獲取最高位的基數
• 2.按位分組，存入桶中
• 3.組內元素數量>1,下一位遞歸分組
• 4.組內元素數量=1.收集元素

   /*** 基數排序--MSD--遞歸* @param array*/public static void radixSortMSD(int[] array) {//1.求出最大數int MAX = array[0];for (int i = 1; i < array.length; i++) {if (array[i] > MAX) {MAX = array[i];}}//求最大值的位數，先變成字符串，求字符串長度int MAXCount = (MAX + "").length();// 計算最大值的基數int radix = new Double(Math.pow(10, MAXCount - 1)).intValue();int[] arr = msdSort(array, radix);System.out.println(Arrays.toString(arr));}public static int[] msdSort(int[] arr, int radix){// 遞歸分組到個位，退出if (radix <= 0) {return arr;}// 分組計數器int[] groupCounter = new int[10];// 分組桶int[][] groupBucket = new int[10][arr.length];for (int i = 0; i < arr.length; i++) {// 找分組桶位置int position = arr[i] / radix % 10;// 將元素存入分組groupBucket[position][groupCounter[position]] = arr[i];// 當前分組計數加1groupCounter[position]++;}int index = 0;int[] sortArr = new int[arr.length];// 遍歷分組計數器for (int i = 0; i < groupCounter.length; i++) {// 組內元素數量>1，遞歸分組if (groupCounter[i] > 1) {int[] copyArr = Arrays.copyOf(groupBucket[i], groupCounter[i]);// 遞歸分組int[] tmp = msdSort(copyArr, radix / 10);// 收集遞歸分組后的元素for (int j = 0; j < tmp.length; j++) {sortArr[index++] = tmp[j];}} else if (groupCounter[i] == 1) {// 收集組內元素數量=1的元素sortArr[index++] = groupBucket[i][0];}}return sortArr;}

基數排序VS基數排序VS桶排序

• 都是非比較型排序

• 三種排序算法都利用了桶的概念

  1.計數排序：每個桶只存儲單一鍵值；

  2.基數排序：根據鍵值的每位數字來分配桶

  3.桶排序： 每個桶存儲一定范圍的數值；

點擊移步博客主頁，歡迎光臨~