AB測試是用來評估變更效果的有效方法,但很多時候會運行大量AB測試,如果能夠在測試中復用之前測試的結果,將有效提升AB測試的效率和有效性。原文: Bayesian AB Testing[1]

隨機實驗,又稱AB測試,是行業中評估因果效應的既定標準。將新方法(新產品、功能、UI等)隨機分配給人群中的特定子集(用戶、患者、客戶等),從而確保平均來說,結果的差異(收入、訪問量、點擊量等)可以歸因于不同的方法。像Booking.com[2]這樣的老牌公司報告說,他們會同時運行數千個AB測試。而多鄰國(Duolingo)[3]等新興公司的成功很大程度上要歸功于他們的大規模實驗文化。
做了這么多實驗,自然而然出現了一個問題: 在某個具體實驗中,能不能利用以前的測試信息?如何利用?在這篇文章中,我們將嘗試通過介紹AB測試的貝葉斯方法來回答這些問題。貝葉斯框架很適合這種類型的任務,允許使用新數據更新現有(先驗)知識。然而,該方法對函數形式假設特別敏感,模型選擇(如先驗分布的偏度)的微小區別可以造成非常不同的估算結果。
搜索和無限滾動
在本文其余部分,我們將使用一個玩具示例,該示例受到Azavedo等人(2019)[4]的啟發: 搜索引擎希望在不犧牲搜索質量的情況下增加廣告收入。我們是一家擁有成熟實驗文化的公司,不斷測試如何改進登錄頁面的新想法。假設我們想出了一個絕妙的新想法: 無限滾動[5]!如果用戶想看到更多結果,他們可以繼續向下滾動,而不是顯示離散的頁面序列。

我們通過AB測試了解無限滾動是否有效: 我們將用戶隨機分為測試組和對照組,只對測試組用戶實施無限滾動。我們從```src.dgp```[6]導入數據,生成dgp_infinite_scroll()。對于以前的文章,我們生成了新的DGP父類,處理隨機化和數據生成,其子類包含了具體用例。我們還從```src.utils```[7]中導入了繪圖函數和庫。為了不僅包含代碼,還包括數據和表格,我們使用Deepnote[8],一個類似于Jupyter的網絡協作筆記本環境。
from?src.utils?import?*
from?src.dgp?import?DGP,?dgp_infinite_scroll
dgp?=?dgp_infinite_scroll(n=10_000)
df?=?dgp.generate_data(true_effect=0.14)
df.head()
| past_revenue | infinite_scroll | ad_revenue | |
|---|---|---|---|
| 0 | 3.76 | 1 | 3.70 |
| 1 | 2.40 | 1 | 1.71 |
| 2 | 2.98 | 1 | 4.85 |
| 3 | 4.24 | 1 | 4.57 |
| 4 | 3.87 | 0 | 3.69 |
我們有1萬名網站訪問者信息,觀察他們每月產生的ad_revenue,考慮是否被分配到測試組并使用infinite_scroll,以及每月平均past_revenue。
隨機測試分配使得均數差(difference-in-means) 估算器沒有偏差[9]。我們期望測試組和對照組平均來看具有可比性,因此可以將觀察到的平均結果差異歸因于測試效果,然后用線性回歸估計測試效果,從而可以將測試效果解釋為infinite_scroll的作用。
smf.ols('ad_revenue ~ infinite_scroll', df).fit().summary().tables[1]

看起來infinite_scroll確實是個好主意,增加了0.1524美元的月平均收益。此外,在1%的置信水平下,該效應顯著高于零。
我們可以通過在回歸中控制past_revenue來進一步提高估算器精度。我們不期望估算系數有明顯變化,但精度應該會提高(如果想了解更多關于控制變量的信息,請查看關于CUPED[10]和DAG[11]的其他文章)。
reg?=?smf.ols('ad_revenue?~?infinite_scroll?+?past_revenue',?df).fit()
reg.summary().tables[1]
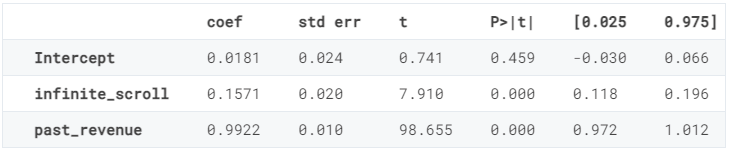
事實上,past_revenue可以準確預測當前ad_revenue,而infinite_scroll估算系數的精度降低了三分之一。
到目前為止,一切都很正常。然而,正如開頭所說,假設這不是我們為改進瀏覽器(并最終提高廣告收入)而進行的唯一實驗,無限滾動只是我們過去測試過的數千個想法中的一個,有沒有一種方法可以有效利用這些額外信息?
貝葉斯統計
貝葉斯統計相對于頻率論方法(frequentist approach)的主要優勢之一是可以比較容易的將額外信息合并到模型中,該想法來源于貝葉斯統計背后的貝葉斯定理(Bayes Theorem)[12],貝葉斯定理允許我們通過反轉推理問題對模型進行推理: 從給定數據的模型的概率,到給定模型的數據的概率,從而使該對象更容易被處理。

可以把貝葉斯定理的右邊分成兩個部分: 先驗(prior) 和可能性(likelihood) ,可能性來自數據關于模型的信息,先驗則是關于模型的任何附加信息。
首先,我們把貝葉斯定理映射到環境中,明確數據是什么、模型是什么、我們感興趣的對象是什么。
-
數據(data) 包括結果變量 ad_revenue(表示為 y),測試變更infinite_scroll(表示為 D和其他變量),past_revenue和常量共同表示為 X -
模型(model) 是在給定 past_revenue和infinite_scroll特性的條件下,ad_revenue的分布,表示為 y|D,X -
感興趣的對象是得到的 Pr(model|data) ,特別是 ad_revenue和infinite_scroll之間的關系
X?=?sm.add_constant(df[['past_revenue']].values)
D?=?df['infinite_scroll'].values
y?=?df['ad_revenue'].values
如何在AB測試上下文中使用可能包含了額外協變量的先驗信息?
貝葉斯回歸
我們用線性模型來直接與頻率論方法進行比較:
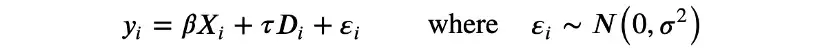
這是一個參數模型,有兩組參數: 線性系數β和τ,以及殘差方差σ。等價但更符合貝葉斯模型的寫法是:
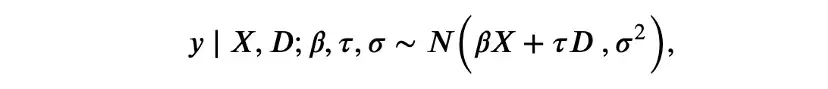
其中半列將數據與模型參數分開。與頻率論方法不同,在貝葉斯回歸中,不依賴中心極限定理[13]來近似y的條件分布,而是直接假設它是正態分布。
我們感興趣的是對模型參數β、τ和σ進行推理。頻率方法和貝葉斯方法的另一個核心區別是,前者假設模型參數是固定、未知的,而后者允許參數是隨機變量。
這個假設有非常實際的含義: 可以很容易的以先驗分布的形式合并關于模型參數的先驗信息。顧名思義,先驗包含了查看數據之前的可用信息。這就引出了貝葉斯統計中最重要的一個相關問題: 如何選擇先驗信息?
先驗信息
選擇先驗信息時,一個有吸引力的限制是確定先驗分布,使得后驗信息屬于同一家族,這叫做共軛先驗(conjugate priors) 。例如,在看到數據之前,假設測試效果是正態分布的,在結合數據中包含的信息后,我們希望它也是正態分布的。
在貝葉斯線性回歸的情況下,β、τ和σ的共軛先驗是正態分布和逆伽瑪分布,我們選擇從標準正態和逆伽馬分布開始。
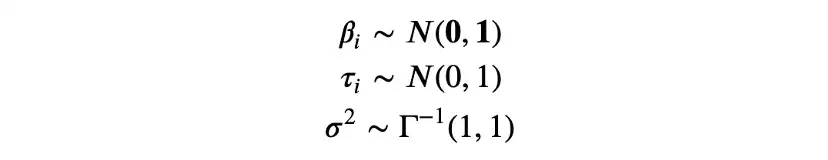
我們用概率編程包PyMC[14]進行推理。首先,需要指定模型: 不同參數的先驗分布和數據的可能性。
import?pymc?as?pm
with?pm.Model()?as?baseline_model:
????#?Priors
????beta?=?pm.MvNormal('beta',?mu=np.ones(2),?cov=np.eye(2))
????tau?=?pm.Normal('tau',?mu=0,?sigma=1)
????sigma?=?pm.InverseGamma('sigma',?mu=1,?sigma=1,?initval=1)
????
????#?Likelihood?
????Ylikelihood?=?pm.Normal('y',?mu=(X@beta?+?D@tau).flatten(),?sigma=sigma,?observed=y)
PyMC有一個非常好的函數model_to_graphviz,允許我們將模型可視化為圖形。
pm.model_to_graphviz(baseline_model)
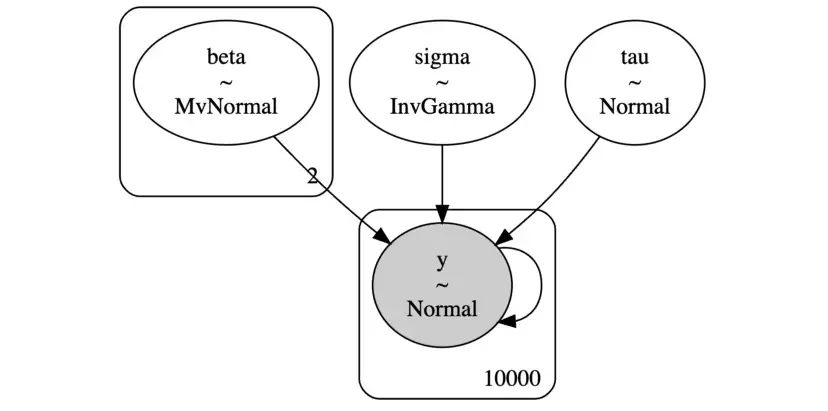
從圖中可以看到各種模型組件、分布,以及如何相互作用。
現在準備計算模型的后驗。我們對模型參數的實現進行抽樣,計算給定值的數據的可能性,并推導出相應的后驗。
idata?=?pm.sample(model=baseline_model,?draws=1000)
貝葉斯推理需要抽樣,這在歷史上一直是貝葉斯統計的主要瓶頸之一,因為它比頻率論方法要慢得多。然而,隨著計算機模型計算能力的增強,這已不再是問題。
現在準備檢查結果。首先,使用summary()方法,可以打印與用于線性回歸的```statmodels```[15]包生成的模型摘要非常相似的模型摘要。
pm.summary(idata,?hdi_prob=0.95).round(4)
| mean | sd | hdi_2.5% | hdi_97.5% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| beta[0] | 0.019 | 0.025 | -0.031 | 0.068 | 0.001 | 0.0 | 1943.0 | 1866.0 | 1.0 |
| beta[1] | 0.992 | 0.010 | 0.970 | 1.011 | 0.000 | 0.0 | 2239.0 | 1721.0 | 1.0 |
| tau | 0.157 | 0.021 | 0.117 | 0.197 | 0.000 | 0.0 | 2770.0 | 2248.0 | 1.0 |
| sigma | 0.993 | 0.007 | 0.980 | 1.007 | 0.000 | 0.0 | 3473.0 | 2525.0 | 1.0 |
估算的參數與頻率論方法得到的參數非常接近,infinite_scroll的估算效果等于0.157。
如果取樣的缺點是速度慢,那么優點是非常透明,可以直接畫出后驗的分布。我們來計算一下測試效應τ,PyMC函數plot_posterior繪制后驗分布,黑色條表示貝葉斯等價的95%置信區間。
pm.plot_posterior(idata,?kind="hist",?var_names=('tau'),?hdi_prob=0.95,?figsize=(6,?3),?bins=30);?
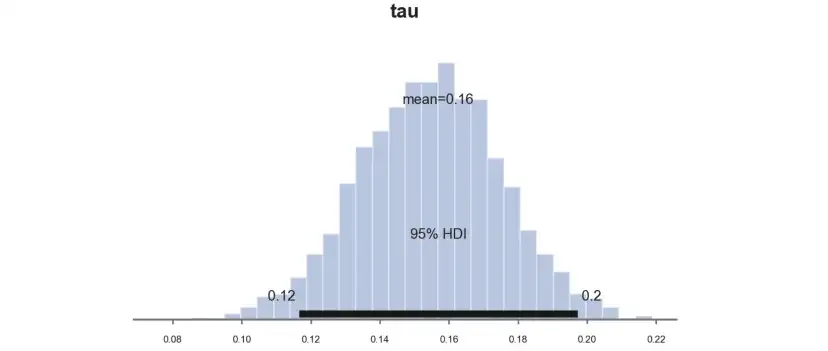
和預期一樣,由于我們選擇了共軛先驗,后驗分布看起來是高斯分布。
目前為止,我們并沒有對選擇先驗施加太多指導。然而,假設我們可以查閱過去的實驗,如何整合這些特定信息?
過去的實驗
假設無限滾動的想法只是我們過去嘗試和測試過的眾多想法中的一個,對于每個想法,都有相應的實驗數據,以及相應的估算系數。
past_experiments?=?[dgp.generate_data(seed_data=i)?for?i?in?range(1000)]
taus?=?[smf.ols('ad_revenue?~?infinite_scroll?+?past_revenue',?pe).fit().params.values?for?pe?in?past_experiments]
我們從過去實驗中得出了1000個估算值,那如何使用這些額外的信息呢?
常態先驗
第一個想法可能是校準先驗,以反映過去的數據分布。我們維持正態假設,使用過去實驗估算的平均值和標準差。
taus_mean?=?np.mean(taus,?axis=0)[1]
taus_mean計算結果為0.0009094486420266667,意味著平均而言,對ad_revenue幾乎沒有影響,平均影響為0.0009。
taus_std?=?np.sqrt(np.cov(taus,?rowvar=0)[1,1])
taus_std計算結果為0.029014447772168384,意味著各實驗之間存在明顯的變化,標準偏差為0.029。
重寫模型,使用過去估算τ的先驗分布均值和標準差。
with?pm.Model()?as?model_normal_prior:
????#?Priors
????beta?=?pm.MvNormal('beta',?mu=np.ones(2),?cov=np.eye(2))
????tau?=?pm.Normal('tau',?mu=taus_mean,?sigma=taus_std)
????sigma?=?pm.InverseGamma('sigma',?mu=1,?sigma=1,?initval=1)
????#?Likelihood
????Ylikelihood?=?pm.Normal('y',?mu=(X@beta?+?D@tau).flatten(),?sigma=sigma,?observed=y)
從模型中取樣:
idata_normal_prior?=?pm.sample(model=model_normal_prior,?draws=1000)
并繪制參數τ的樣本后驗分布處理效果圖。
pm.plot_posterior(idata_normal_prior,?kind="hist",?var_names=('tau'),?hdi_prob=0.95,?figsize=(6,?3),?bins=30);?
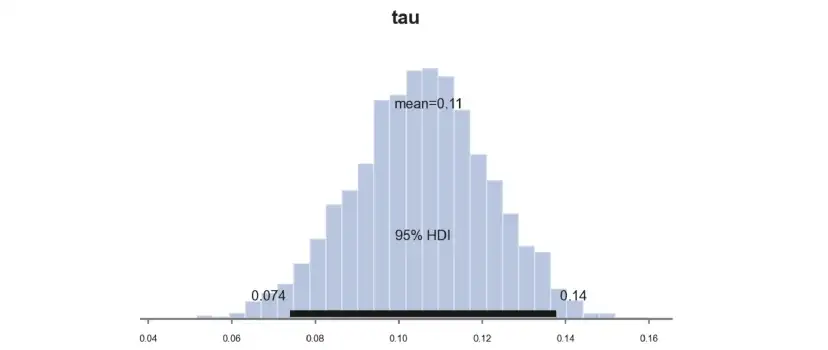
估算系數明顯較小,為0.11,而不是先前估算的0.16。為什么會這樣呢?
事實是,考慮到我們的先驗,之前的系數0.16是極不可能的。在給定先驗條件下,可以計算得到相同或更極端值的概率。
1?-?sp.stats.norm(taus_mean,?taus_std).cdf(0.16)
計算結果為2.0532795019789774e-08,概率幾乎為零。因此,估算系數已經向先前的平均值0.0009移動。
T先驗(Student-t Prior)
目前為止,我們假設所有線性系數都是正態分布。這樣合適嗎?讓我們從截距系數(intercept coefficient) 開始直觀檢查。
sns.histplot([tau[0]?for?tau?in?taus]).set(title=r'Distribution?of?$\hat{\beta}_0$?in?past?experiments');
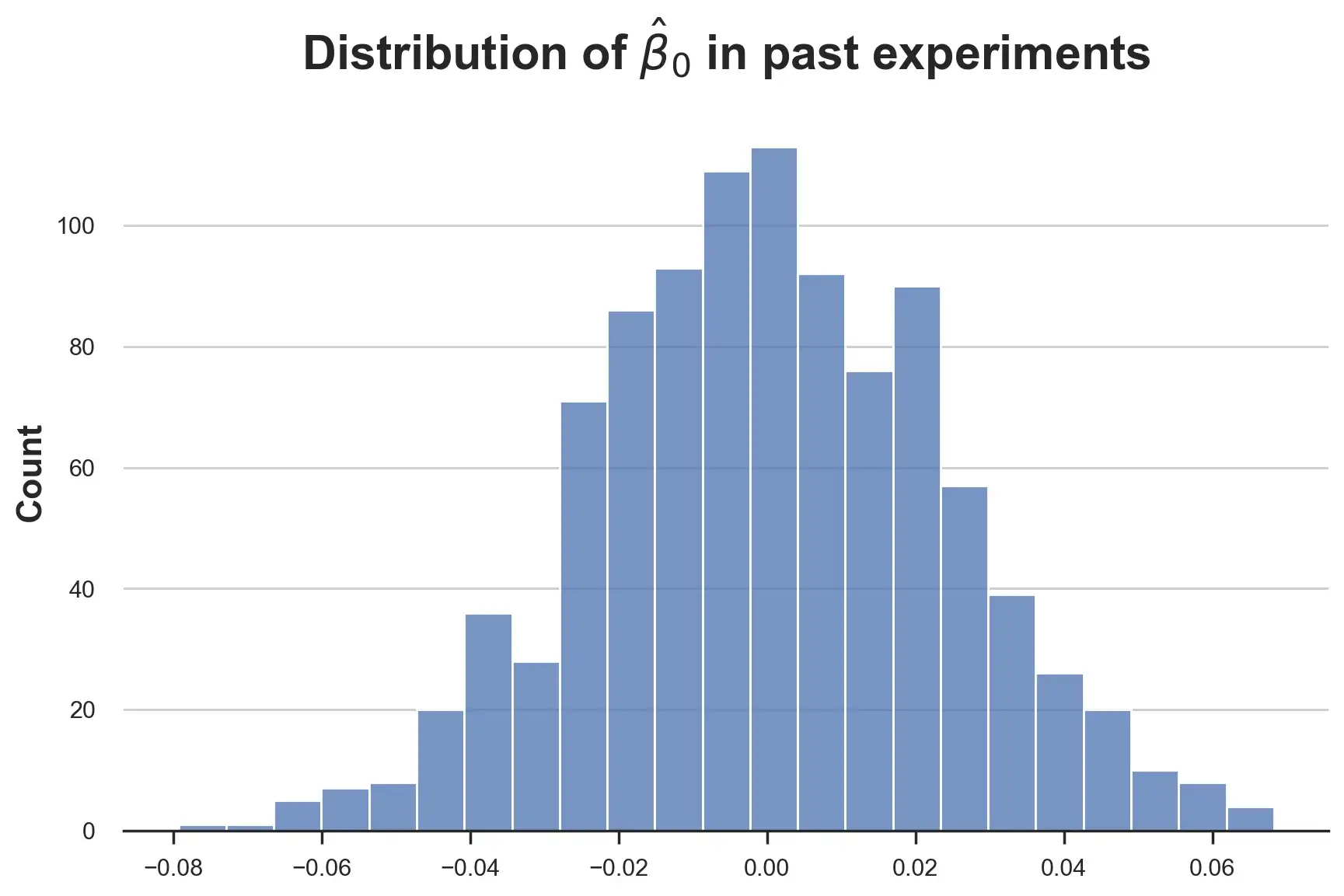
分布似乎很正常,那么效果參數τ呢?
fig,?ax?=?plt.subplots()
sns.histplot([tau[1]?for?tau?in?taus],?label='past?experiments');
ax.axvline(reg.params['infinite_scroll'],?lw=2,?c='C3',?ls='--',?label='current?experiment')
plt.legend();
plt.title(r'Distribution?of?$\hat{\tau}$?in?past?experiments');
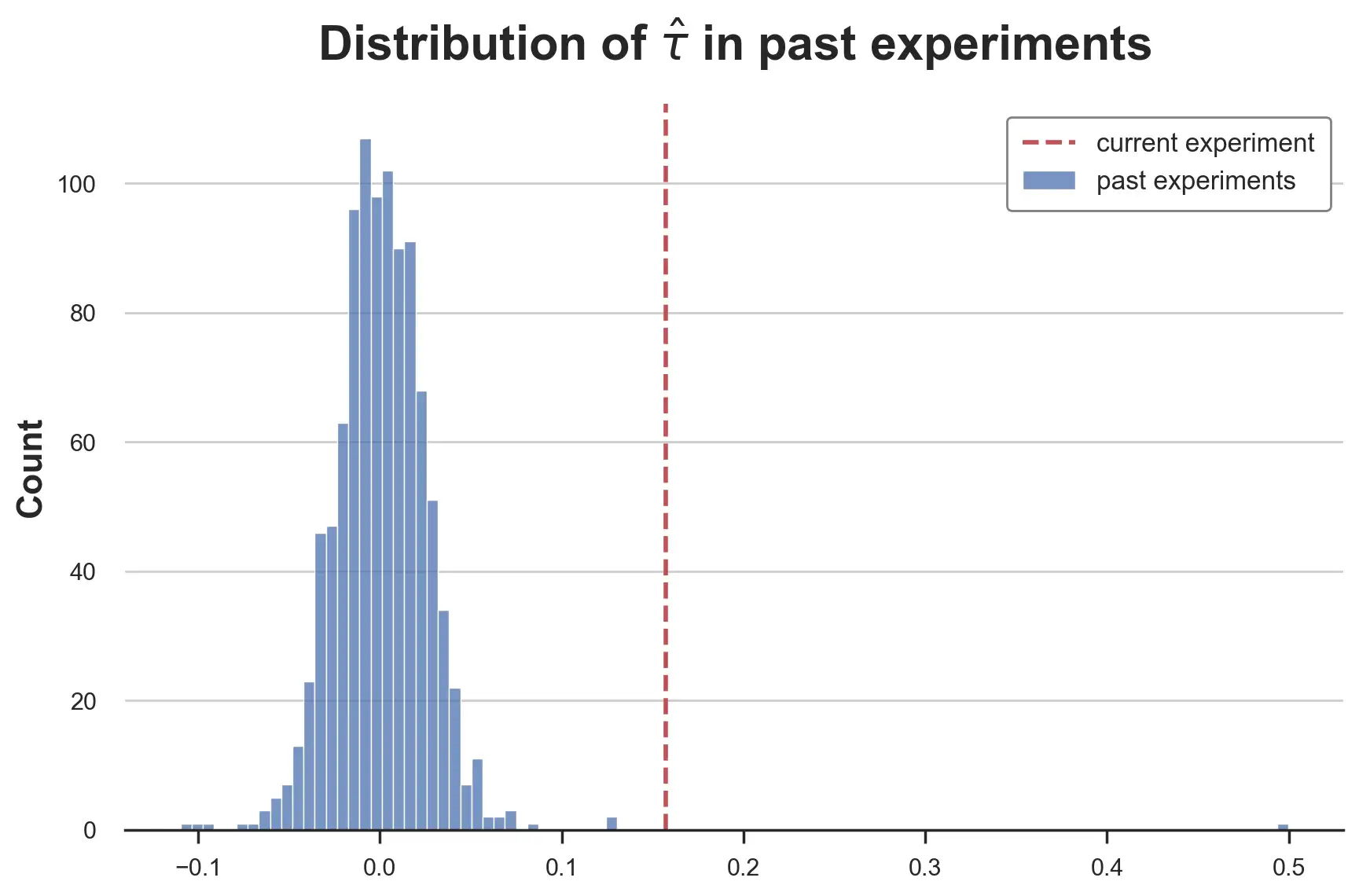
這是一個非常肥尾(heavy-tailed) 的分布,在中心看起來像正態分布,尾部更"胖",有兩個非常極端的值。排除測量誤差,這是行業中經常發生的情況,大多數想法的影響都非常小或為零,很少有想法是突破性的。
模擬這種分布的一種方法是T分布(student-t)[16]。我們用均值為0.0009,方差為0.003,自由度為1.3的T分布來匹配過去估算的經驗分布矩陣。
with?pm.Model()?as?model_studentt_prior:
????#?Priors
????beta?=?pm.MvNormal('beta',?mu=np.ones(2),?cov=np.eye(2))
????tau?=?pm.StudentT('tau',?mu=taus_mean,?sigma=0.003,?nu=1.3)
????sigma?=?pm.InverseGamma('sigma',?mu=1,?sigma=1,?initval=1)
????
????#?Likelihood?
????Ylikelihood?=?pm.Normal('y',?mu=(X@beta?+?D@tau).flatten(),?sigma=sigma,?observed=y)
從模型中取樣。
idata_studentt_priors?=?pm.sample(model=model_studentt_prior,?draws=1000)
并繪制參數τ的樣本后驗分布處理效果圖。
pm.plot_posterior(idata_studentt_priors,?kind="hist",?var_names=('tau'),?hdi_prob=0.95,?figsize=(6,?3),?bins=30);?
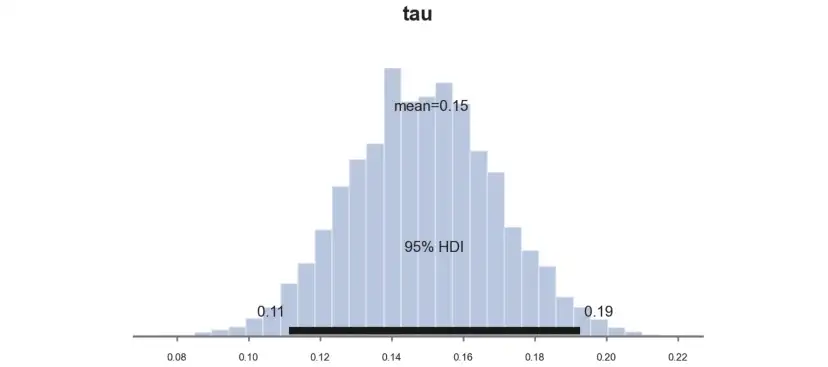
估算系數類似于用標準先驗得到的系數0.11,然而由于置信區間從[0.077,0.016]縮小到[0.065,0.015],估算更加精確。
發生了什么?
收縮
答案在于所用的不同先驗分布形態:
-
標準正態,N(0,1) -
正態矩匹配,N(0,0.03) -
T型匹配矩陣, (0, 0.003)
t_hats?=?np.linspace(-0.3,?0.3,?1_000)
distributions?=?{
????'N(0,1)':?sp.stats.norm(0,?1).pdf(t_hats),
????'N(0,?0.03)':?sp.stats.norm(0,?0.03).pdf(t_hats),
????'$t_{1.3}$(0,?0.003)':?sp.stats.t(df=1.3).pdf(t_hats?/?0.003)*300,
}
畫在一起看看。
for?i,?(label,?y)?in?enumerate(distributions.items()):
????sns.lineplot(x=t_hats,?y=y,?color=f'C{i}',?label=label);
plt.xlim(-0.15,?0.15);
plt.legend();?
plt.title('Prior?Distributions');
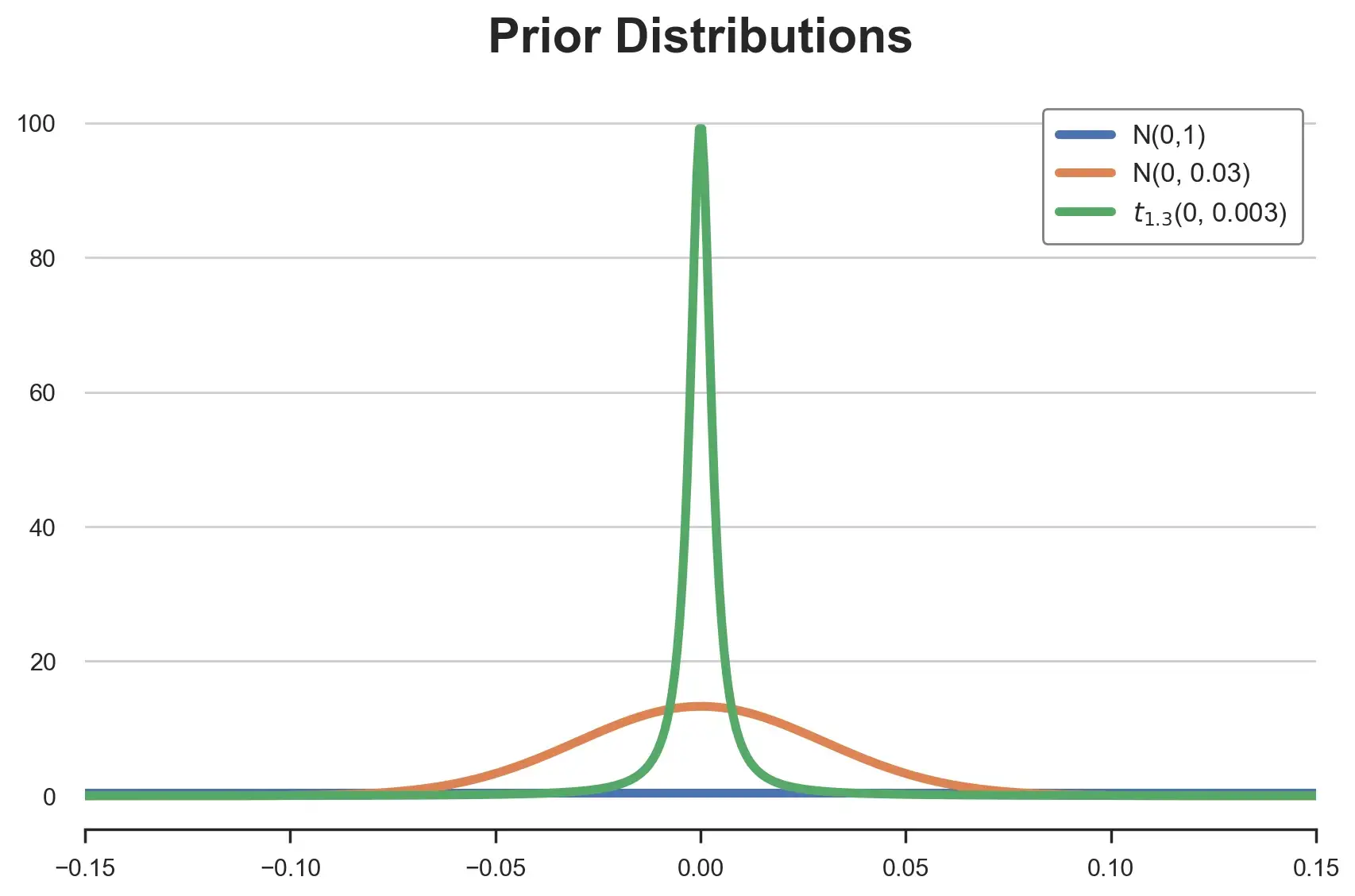
正如我們所看到的,所有分布都以0為中心,但形狀非常不同。標準正態分布在[-0.15,0.15]區間內基本上是平坦的,每個值的概率基本相同。而后兩個盡管有相同的均值和方差,但形態非常不同。
這如何轉化為我們的估算?對每個先驗分布,可以畫出不同估算的隱含后驗。
fig,?ax?=?plt.subplots(figsize=(7,6))
ax.axvline(reg.params['infinite_scroll'],?lw=2,?ls='--',?c='darkgray');
for?i,?(label,?y)?in?enumerate(distributions.items()):
????sns.lineplot(x=t_hats,?y=[compute_posterior(t,?y)?for?t?in?t_hats]?,?color=f'C{i}',?label=label);
plt.legend();?
ax.set_xlabel('Experiment?Estimate');
ax.set_ylabel('Posterior');
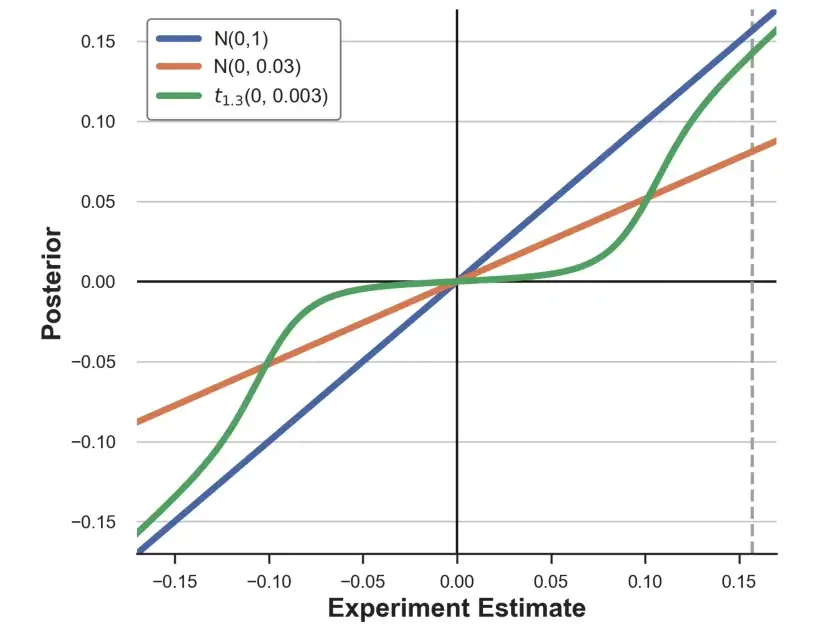
正如我們所看到的,不同的先驗以非常不同的方式改變實驗估算。標準正態先驗基本上對[-0.15,0.15]區間內的估算沒有影響。具有匹配矩陣的正常先驗反而使每個估算值縮小約2/3。T先驗的影響是非線性的: 將小估算縮小到零,而保持大估算不變。灰色虛線標記了不同先驗對實驗估算τ的影響。

結論
通過本文,我們了解了如何擴展AB測試的分析,以合并來自過去實驗的信息。我們特別介紹了AB測試的貝葉斯方法,看到選擇先驗分布的重要性。在相同均值和方差下,假設存在"肥尾"(非常偏斜)的先驗分布,意味著小效應的收縮更強,而大效應的收縮更少。
直覺上,帶有"肥尾"的先驗分布相當于假設突破性想法是罕見的,但不是不可能。正如我們在這篇文章中所看到的,這在實驗后有實際意義,但在實驗前也有意義。事實上,正如Azevedo等人(2020)[17]所報告的那樣,如果你認為想法的效果分布比較"正常",那么最好是進行少量但大型的實驗,以便能夠發現較小的效果。相反,如果你認為想法是"要么是突破性的,要么毫無意義",即效果是肥尾的,那么運行小而多的實驗更有意義,因為不需要大規模實驗來檢測大的效果。
代碼
本文所有代碼都在Jupyter Notebook上: https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/bayes_ab.ipynb。
你好,我是俞凡,在Motorola做過研發,現在在Mavenir做技術工作,對通信、網絡、后端架構、云原生、DevOps、CICD、區塊鏈、AI等技術始終保持著濃厚的興趣,平時喜歡閱讀、思考,相信持續學習、終身成長,歡迎一起交流學習。
微信公眾號:DeepNoMind
參考資料
Bayesian AB Testing: https://towardsdatascience.com/bayesian-ab-testing-ed45cc8c964d
[2]The role of experimentation at Booking.com: https://partner.booking.com/en-gb/click-magazine/industry-perspectives/role-experimentation-bookingcom
[3]Improving Duolingo, one experiment at a time: https://blog.duolingo.com/improving-duolingo-one-experiment-at-a-time
[4]Empirical Bayes Estimation of Treatment Effects with Many A/B Tests: An Overview: https://www.aeaweb.org/articles?id=10.1257/pandp.20191003
[5]Continuous scrolling comes to Search on mobile: https://blog.google/products/search/continuous-scrolling-mobile
[6]src.dgp: https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/src/dgp.py
src.utils: https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/src/utils.py
Deepnote: https://deepnote.com
[9]Bias of an estimator: https://en.wikipedia.org/wiki/Bias_of_an_estimator
[10]Understanding CUPED: https://towardsdatascience.com/understanding-cuped-a822523641af
[11]DAGs and Control Variables: https://towardsdatascience.com/controls-b63dc69e3d8c
[12]貝葉斯定理(Bayes Theorem): https://en.wikipedia.org/wiki/Bayes'_theorem
[13]中心極限定理: https://en.wikipedia.org/wiki/Central_limit_theorem
[14]PyMC: https://www.pymc.io/projects/docs/en/stable/learn.html
[15]statmodels: https://www.statsmodels.org/dev/index.html
T分布(student-t): https://en.wikipedia.org/wiki/Student%27s_t-distribution
[17]A/B Testing with Fat Tails: https://www.journals.uchicago.edu/doi/full/10.1086/710607
本文由 mdnice 多平臺發布

![【Mysql】[Err] 1293 - Incorrect table definition;](http://pic.xiahunao.cn/【Mysql】[Err] 1293 - Incorrect table definition;)

















-創建者模式(4)-原型模式)