LeetCode 面試經典 150 題：輪轉數組（三次翻轉法詳解 + 多解法對比）

在數組類算法題中，“輪轉數組” 是一道考察 “原地操作” 與 “邏輯轉換” 能力的經典題目。所謂 “輪轉”，是指將數組元素向右移動指定步數，且超出數組長度的元素需 “循環” 到數組開頭。這道題的最優解 ——三次翻轉法，能以 O (n) 時間復雜度和 O (1) 空間復雜度實現原地輪轉，是面試中高頻考察的高效思路。本文將從題目解讀、三次翻轉法原理、步驟演示，到代碼實現，再到其他解法對比，幫你徹底掌握這道題的核心邏輯。

一、題目鏈接與題干解讀

首先，你可以通過以下鏈接直接訪問題目，先自行思考解題方向：

LeetCode 題目鏈接：189.?輪轉數組

題干核心信息

題目要求如下：

給定一個整數數組 nums，將數組中的元素向右輪轉 k 個位置，其中 k 是非負數。

例如，若 nums = [1,2,3,4,5,6,7]，k = 3，則輪轉后數組為 [5,6,7,1,2,3,4]。

關鍵注意點

k 的取值范圍：k 可能大于數組長度 n，此時輪轉效果與 “k 對 n 取模” 后的結果一致（例如 n=7，k=10，10 mod 7=3，輪轉 10 步與輪轉 3 步結果相同）；

原地操作要求：若想達到最優空間復雜度，需避免開辟新數組，在原數組上完成輪轉；

元素順序保留：輪轉后，元素的相對順序需保持（如示例中 5、6、7 的相對順序，1、2、3、4 的相對順序均不變）。

二、核心解法：三次翻轉法（原地高效）

三次翻轉法的核心思想是 “通過翻轉操作，將‘向右輪轉’的復雜邏輯轉化為三次簡單的數組翻轉”。其本質是利用翻轉對元素順序的改變，間接實現輪轉效果，且全程無需開辟新數組，空間復雜度極低。

1. 為什么需要先對 k 取模？

由于數組輪轉 n 步后會回到原始狀態（例如 n=7，輪轉 7 步后數組不變），因此當 k≥n 時，實際需要的輪轉步數為 k_mod = k % n。這一步操作能減少不必要的計算（例如 k=10 時，只需處理 3 步而非 10 步），是優化解題的關鍵前提。

例如：

當 n=7，k=3 時，k_mod=3，無需調整；

當 n=7，k=10 時，k_mod=10%7=3，按 3 步處理；

當 n=7，k=7 時，k_mod=0，無需輪轉（數組不變）。

2. 三次翻轉的邏輯原理

我們先明確 “向右輪轉 k 步” 的效果：數組末尾的 k 個元素會移動到數組開頭，其余元素向右順延。例如，數組[a1,a2,a3,a4,a5,a6,a7]（n=7），向右輪轉 3 步后為[a5,a6,a7,a1,a2,a3,a4]—— 末尾 3 個元素[a5,a6,a7]到開頭，前 4 個元素[a1,a2,a3,a4]順延。

三次翻轉法通過以下步驟實現這一效果：

翻轉整個數組：將數組從 “前 n-k 個元素 + 后 k 個元素” 的結構，變為 “后 k 個元素的逆序 + 前 n-k 個元素的逆序”；

翻轉前 k 個元素：將 “后 k 個元素的逆序” 恢復為原順序，此時前 k 個元素就是輪轉后需要放在開頭的元素；

翻轉后 n-k 個元素：將 “前 n-k 個元素的逆序” 恢復為原順序，此時后 n-k 個元素就是輪轉后需要放在末尾的元素。

簡單來說，三次翻轉的邏輯鏈是：整體翻轉打亂順序→局部翻轉恢復目標區域順序→最終得到輪轉結果。

3. 示例演示（以nums = [1,2,3,4,5,6,7]，k=3為例）

步驟 1：計算 k_mod

n=7，k=3，k_mod=3%7=3。

步驟 2：第一次翻轉（翻轉整個數組）

原數組：[1,2,3,4,5,6,7]

翻轉后：[7,6,5,4,3,2,1]

作用：將末尾的 3 個元素（5,6,7）翻轉為（7,6,5），移到數組前半部分；將前 4 個元素（1,2,3,4）翻轉為（4,3,2,1），移到數組后半部分。

步驟 3：第二次翻轉（翻轉前 k_mod=3 個元素）

當前數組：[7,6,5,4,3,2,1]

翻轉前 3 個元素：[5,6,7,4,3,2,1]

作用：將前 3 個元素（7,6,5）恢復為原順序（5,6,7），這正是輪轉后需要放在開頭的元素。

步驟 4：第三次翻轉（翻轉后 n-k_mod=4 個元素）

當前數組：[5,6,7,4,3,2,1]

翻轉后 4 個元素：[5,6,7,1,2,3,4]

作用：將后 4 個元素（4,3,2,1）恢復為原順序（1,2,3,4），這正是輪轉后需要放在末尾的元素。

最終結果與題目預期完全一致，驗證了三次翻轉法的正確性。

4. 翻轉操作的實現

翻轉數組的某一段（從索引 left 到索引 right）是三次翻轉法的基礎操作，實現邏輯如下：

初始化兩個指針，left 指向段的起始索引，right 指向段的結束索引；

交換 left 和 right 指向的元素，然后 left 向右移動 1 位，right 向左移動 1 位；

重復上述操作，直到 left ≥ right（即指針相遇或交叉，段內元素全部交換完畢）。

例如，翻轉數組[7,6,5]（left=0，right=2）：

交換 7 和 5 → [5,6,7]，left=1，right=1；

left ≥ right，翻轉結束。

三、其他常見解法（對比參考）

除了三次翻轉法，“輪轉數組” 還有其他解法，雖然復雜度不如三次翻轉法最優，但能幫助我們從不同角度理解問題，以下簡要介紹兩種：

1. 額外數組法（空間復雜度 O (n)）

思路

開辟一個與原數組長度相同的新數組，將原數組中 “需要輪轉的元素” 按目標順序放入新數組，最后將新數組的值復制回原數組。

對于原數組索引 i 的元素，輪轉后在新數組的索引為 (i + k) % n（向右輪轉 k 步）；

也可直接定位：新數組前 k 個元素對應原數組末尾 k 個元素（索引 n-k 到 n-1），新數組后 n-k 個元素對應原數組前 n-k 個元素（索引 0 到 n-k-1）。

優缺點

優點：邏輯直觀，易于理解和實現，無需復雜的翻轉操作；

缺點：需要開辟額外數組，空間復雜度為 O (n)，不如三次翻轉法高效。

2. 多次右移法（時間復雜度 O (nk)）

思路

每次只將數組向右輪轉 1 步，重復 k 次。輪轉 1 步的邏輯是：保存數組最后一個元素，然后將其余元素從后向前依次右移 1 位，最后將保存的元素放到數組開頭。

優缺點

優點：邏輯簡單，無需復雜算法，僅需基礎的元素移動操作；

缺點：時間復雜度為 O (nk)（每次輪轉 1 步需 O (n) 時間，共 k 次），當 k 較大時（如 k=n），時間復雜度會達到 O (n2)，效率極低。

四、復雜度分析（三次翻轉法）

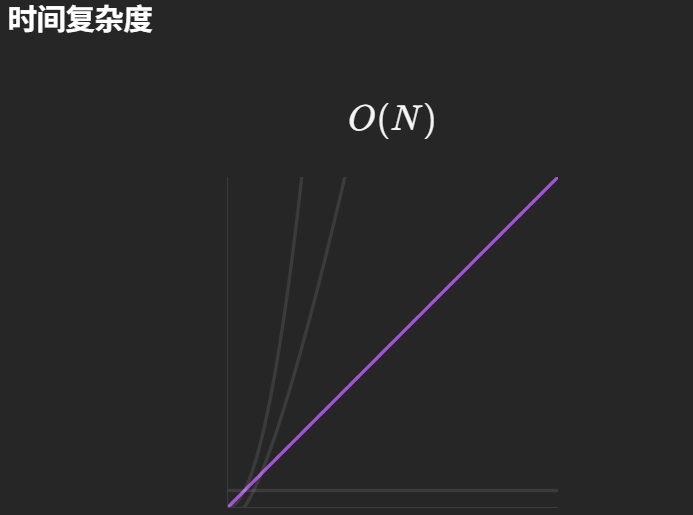
1. 時間復雜度：O (n)

翻轉操作的時間復雜度：翻轉一段長度為 L 的數組，需要交換 L//2 次元素，時間復雜度為 O (L)；

三次翻轉的總時間：第一次翻轉整個數組（O (n)），第二次翻轉前 k 個元素（O (k)），第三次翻轉后 n-k 個元素（O (n-k)），總時間為 O (n) + O (k) + O (n-k) = O (n)；

整體時間：加上 k 取模的 O (1) 操作，總時間復雜度為 O (n)。

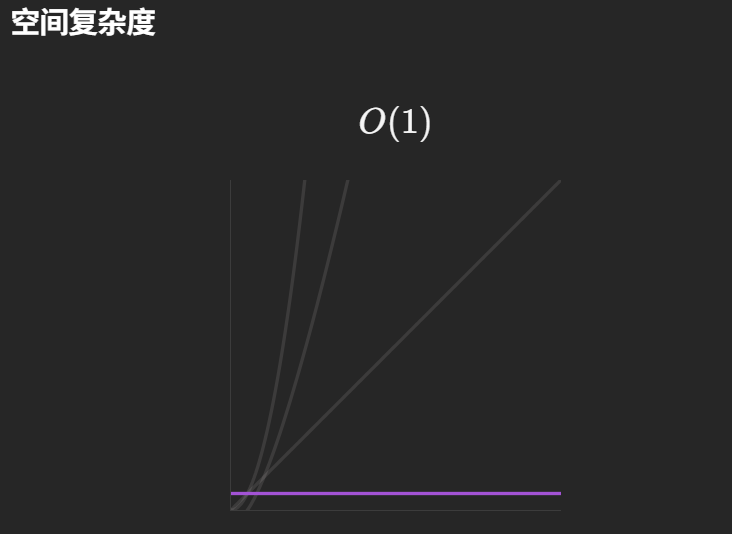
2. 空間復雜度：O (1)

整個過程僅用到了幾個額外變量（如 left、right 指針，k_mod 等），沒有開辟新的數組或其他數據結構；

所有翻轉操作都在原數組上完成，額外空間的使用與數組長度 n 無關，因此空間復雜度為常數級的 O (1)。

五、三次翻轉法代碼實現

以下以 Python，Java 為例，實現三次翻轉法，核心是先實現 “段翻轉” 函數，再執行三次翻轉：

1，Python

class Solution:def rotate(self, nums: List[int], k: int) -> None:def reversed(i: int, j: int):while i < j:nums[i], nums[j] = nums[j], nums[i]i, j = i + 1, j - 1n = len(nums)k %= nreversed(0, n - 1)reversed(0, k - 1)reversed(k, n - 1)

2，Java

class Solution {int[] nums;public void rotate(int[] nums, int k) {this.nums = nums;int n = nums.length;k %= n;reversed(0, n - 1);reversed(0, k - 1);reversed(k, n - 1);}private void reversed(int i, int j) {for (; i < j; i++, j--) {int t = nums[i];nums[i] = nums[j];nums[j] = t;}}
}

你可以將上述代碼復制到 LeetCode 編輯器中測試，完全符合題目要求。