第4章：深度前饋神經網絡（DNN）模型

歡迎回來🐻???

在第1章：分類任務配置（二分類 vs. 多分類）中，我們學習了如何配置模型以回答不同類型的問題；在第2章：數據加載與預處理中，我們成為了“數據大廚”，準備好了數據“食材”；最近，在第3章：經典機器學習模型中，我們探索了一套可靠的“手工工具”來檢測入侵行為。

雖然經典模型非常強大，但有時網絡攻擊極其隱蔽且復雜。它們可能涉及一些細微的模式，簡單的模型難以捕捉。想象一下，我們有一支安全警衛團隊。有些警衛擅長檢查基本的ID（經典模型），但對于真正復雜的威脅，我們需要一個高度專業化、多階段的安全系統，其中包含層層互聯的專家，每位專家在傳遞信息前都會對其進行精煉。

這就是深度前饋神經網絡（DNN）模型的用武之地

這是我們邁向“深度學習”世界的第一步，深度學習是受人類大腦啟發的模型。DNN能夠揭示網絡流量數據中極其復雜、非直觀的關系，使其能夠檢測到最難以捉摸的入侵行為。

DNN解決了什么問題？

DNN旨在學習輸入特征（如連接持續時間、協議、字節計數）與輸出標簽（如“正常”或“攻擊”）之間的復雜非線性關系。經典模型可能難以處理那些無法通過簡單直線或曲線輕松分隔的模式。而DNN通過其多層結構，本質上可以在數據中繪制高度復雜的波浪形邊界，從而更精確地區分不同類型的網絡流量。

我們的核心用例仍然是網絡入侵檢測，但現在我們裝備了一個能夠處理更深層次、更抽象攻擊特征的模型。

DNN的關鍵概念

深度前饋神經網絡通常也稱為多層感知機（MLP）。它之所以“深”，是因為它在輸入和輸出之間有多個隱藏層。“前饋”意味著信息單向流動，從輸入到輸出，不會循環回來。

讓我們分解其核心部分：

1. 神經元（節點）

將神經元想象為一個微小的決策單元。它接收輸入，進行簡單計算，然后將輸出傳遞給下一個神經元。每個輸入都有一個與之關聯的權重（表示該輸入的重要性），神經元還有一個偏置（添加到計算中的額外值）。模型通過調整這些權重和偏置來學習。

2. 層：決策的各個階段

神經元被組織成層，形成我們安全系統的“階段”：

• 輸入層：這是原始處理數據（來自第2章：數據加載與預處理的網絡連接的41個特征）進入網絡的地方。每個特征都有自己的“輸入神經元”。
• 隱藏層（密集層）：這是DNN的核心。它們被稱為“隱藏”是因為它們不直接與外界（輸入或輸出）交互。在這些層中，神經元是“密集連接”的——即一層中的每個神經元都與下一層中的每個神經元相連。這使得它們能夠處理和轉換來自前一層的信息，學習越來越復雜的特征。DNN至少有一個隱藏層，通常有很多。
• 輸出層：這是給出模型預測的最終層。正如我們在第1章：分類任務配置（二分類 vs. 多分類）中學到的，其配置取決于我們是進行二分類（1個神經元，sigmoid激活）還是多分類（N個神經元，softmax激活）。

3. 激活函數：添加非線性

在神經元計算其輸入的加權和加上偏置后，“激活函數”決定是否以及如何“激活”（產生輸出）。

• relu（修正線性單元）：這是隱藏層中非常常見的激活函數。它很簡單：如果輸入為正，則直接輸出；如果為負，則輸出零。這種非線性對于DNN學習復雜模式至關重要，而不僅僅是簡單的直線。
• sigmoid / softmax：如第1章所述，這些是專門用于分類任務的輸出層的激活函數。

4. Dropout層：防止過擬合

想象一下，我們的安全警衛變得過于擅長記住訓練中的特定面孔，但在面對稍有不同新面孔時卻無法識別。這就是過擬合——模型對訓練數據記憶得太好，失去了對新數據的泛化能力。

Dropout層是一個聰明的技巧，可以防止這種情況。在訓練過程中，Dropout層會隨機“關閉”一層中一定比例的神經元。這迫使剩余的神經元學習更魯棒的特征，并防止任何單個神經元過度依賴其他神經元。這就像強制不同的安全警衛輪流休息，確保整個團隊都具備能力，而不是只有一個明星。

如何構建用于入侵檢測的DNN

我們將使用Keras（一個用戶友好的神經網絡構建庫）來構建我們的DNN。基本步驟如下：

1. 啟動一個Sequential模型：這是一個簡單的層堆疊。
2. 添加Dense層：這些是我們的隱藏層，使用relu激活。
3. 添加Dropout層：防止過擬合。
4. 添加Dense輸出層：根據第1章配置為二分類或多分類。
5. 編譯模型：告訴它如何學習（優化器）以及測量什么（損失函數、指標）。
6. 訓練模型：輸入準備好的數據。

讓我們看一個簡化示例。假設X_train包含我們歸一化的網絡特征，y_train包含標簽，如第2章和第1章所述。

示例代碼：用于二分類的簡單DNN

以下是如何構建一個帶有一個隱藏層的基本DNN用于二分類入侵檢測：

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
import numpy as np # 用于數據創建示例# --- 假設 X_train 和 y_train 已從第2章準備好 ---
# 為了演示，我們創建一些虛擬數據：
# 1000個樣本，每個樣本41個特征
X_train_dummy = np.random.rand(1000, 41)
# 1000個二分類標簽（0或1）
y_train_dummy = np.random.randint(0, 2, 1000)# 1. 開始定義網絡（層的堆疊）
model = Sequential()# 2. 添加第一個（也是唯一的）隱藏層：一個Dense層
#    - 1024個神經元（可以自行選擇數量）
#    - input_dim=41：告訴模型輸入有41個特征
#    - activation='relu'：隱藏層的激活函數
model.add(Dense(1024, input_dim=41, activation='relu'))# 3. 添加一個Dropout層
#    - 0.01表示訓練期間隨機“關閉”1%的神經元
model.add(Dropout(0.01))# 4. 添加輸出層（用于二分類，如第1章所述）
#    - 1個神經元用于二分類輸出
#    - activation='sigmoid'：將輸出壓縮為0到1之間的概率
model.add(Dense(1, activation='sigmoid'))# 5. 編譯模型
#    - loss='binary_crossentropy'：用于二分類
#    - optimizer='adam'：一種流行且有效的優化算法
#    - metrics=['accuracy']：訓練期間跟蹤性能
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])print("DNN模型創建并編譯完成！")
model.summary() # 打印模型層的摘要

解釋：

• Sequential()：這為我們的神經網絡創建了一個空白畫布，可以一層一層地堆疊。
• Dense(1024, input_dim=41, activation='relu')：這是我們的第一個主要處理層。它有1024個神經元。input_dim=41對于第一層至關重要，告訴Keras輸入特征的大小。我們使用relu來學習非線性模式。
• Dropout(0.01)：該層通過隨機丟棄1%的神經元連接來防止過擬合。
• Dense(1, activation='sigmoid')：這是最終的決策層。如第1章所述，對于二分類，我們使用1個神經元和sigmoid激活來輸出概率（0到1）。
• model.compile(...)：這為訓練準備模型。loss='binary_crossentropy'測量預測與真實標簽的差距。optimizer='adam'是調整權重以最小化損失的“引擎”。metrics=['accuracy']是我們跟蹤模型表現的指標。

擴展到多層和多分類

為了使DNN“更深”（更多隱藏層），只需添加更多的Dense和Dropout層：

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
# ...（數據準備如前所述）...# 多分類示例：假設 num_classes = 5（正常、DoS、Probe、R2L、U2R）
num_classes = 5
# y_train_dummy 應為 one-hot 編碼，例如 to_categorical(y_train_raw, num_classes=5)model_deep = Sequential()
model_deep.add(Dense(1024, input_dim=41, activation='relu'))
model_deep.add(Dropout(0.01))
model_deep.add(Dense(768, activation='relu')) # 第二個隱藏層
model_deep.add(Dropout(0.01))
model_deep.add(Dense(512, activation='relu')) # 第三個隱藏層
model_deep.add(Dropout(0.01))
# ... 可以添加更多層 ...
model_deep.add(Dense(256, activation='relu')) # 第四個隱藏層
model_deep.add(Dropout(0.01))
model_deep.add(Dense(128, activation='relu')) # 第五個隱藏層
model_deep.add(Dropout(0.01))# 對于多分類（如第1章所述）：
model_deep.add(Dense(num_classes, activation='softmax'))model_deep.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])print("\n用于多分類的深度DNN模型創建并編譯完成！")
model_deep.summary()

多分類的關鍵區別：

• Dense(num_classes, activation='softmax')：輸出層現在有num_classes（例如5）個神經元，softmax激活確保輸出是每個類的概率，總和為1。
• loss='categorical_crossentropy'：當標簽是one-hot編碼時（多分類問題中應該如此，如第1章所述），這是合適的損失函數。

幕后：DNN如何做決策

將DNN想象為一個流水線，信息（網絡流量數據）在最終決策前經過多個階段的精煉和處理。

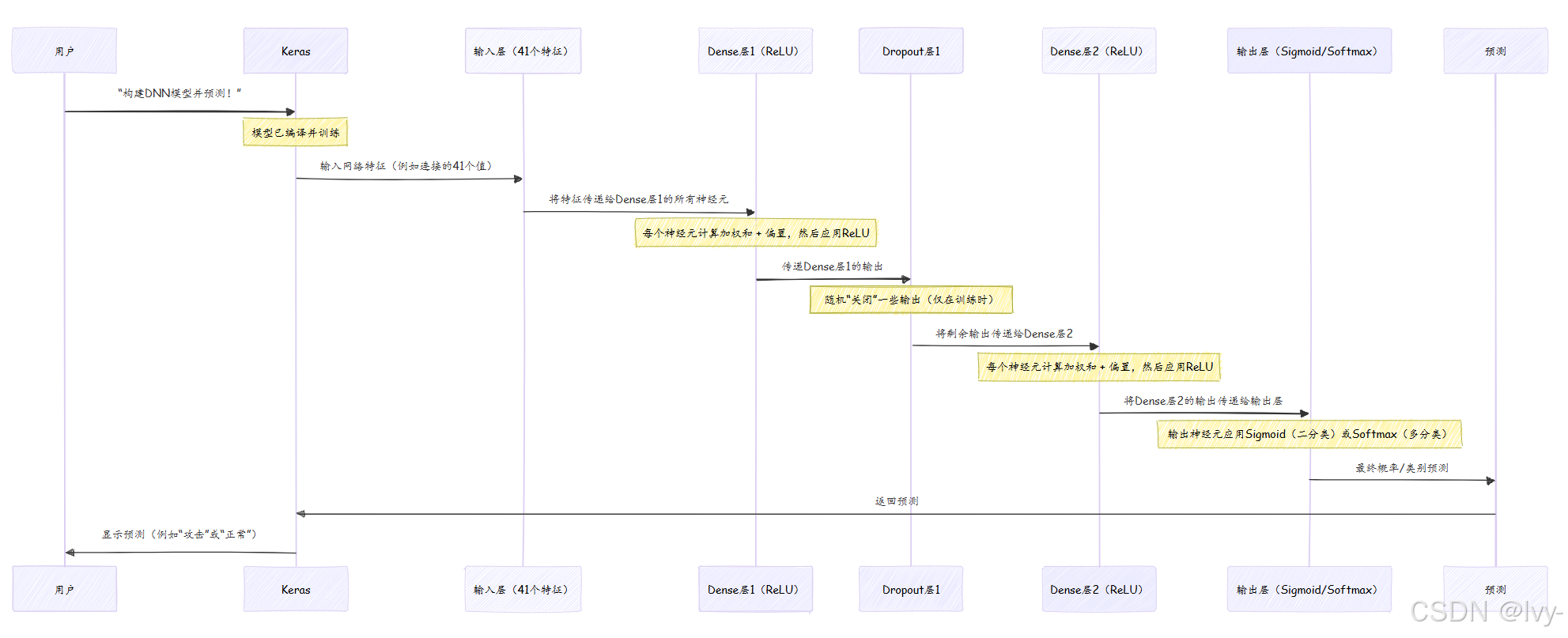
在訓練期間（我們將在第8章：模型訓練生命周期（Keras）中介紹），這個過程會反復進行。每次傳遞后，模型將其預測與真實標簽進行比較，計算loss，然后微妙地調整每個Dense層中的所有權重和偏置，以減少下一次的loss。這種迭代調整就是模型“學習”的方式。

深入項目代碼參考

讓我們看看實際項目代碼文件，了解DNN是如何實現的。你可以在KDDCup 99/dnn/文件夾（以及NSL-KDD、UNSW-NB15等其他數據集的類似文件夾）中找到這些內容。

1. 基本DNN（1個隱藏層）- 二分類

查看KDDCup 99/dnn/binary/dnn1.py或NSL-KDD/dnn/binary/dnn1.py。在數據加載和歸一化步驟（類似于第2章）之后：

# 來自 KDDCup 99/dnn/binary/dnn1.py（簡化版）
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation# ...（X_train, y_train, X_test, y_test 已在此處準備好）...model = Sequential()
# 輸入層（由第一個Dense層的input_dim隱式處理）
# 第一個隱藏層（Dense層1）
model.add(Dense(1024, input_dim=41, activation='relu'))
model.add(Dropout(0.01)) # 隱藏層后的Dropout
# 輸出層（二分類1個神經元，sigmoid激活）
model.add(Dense(1))
model.add(Activation('sigmoid')) # 單獨應用的激活函數model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# ...（訓練時的model.fit調用）...

觀察：

• input_dim=41用于指定數據集中的特征數量。
• 一個Dense層后跟一個Dropout層構成隱藏部分。
• 輸出層使用Dense(1)和Activation('sigmoid')，與第1章中的二分類配置匹配。
• binary_crossentropy是損失函數。

2. 更深DNN（5個隱藏層）- 二分類

現在，我們來看KDDCup 99/dnn/binary/dnn5.py。關鍵區別在于堆疊了多個Dense和Dropout層，使網絡“更深”：

# 來自 KDDCup 99/dnn/binary/dnn5.py（簡化版）
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation# ...（X_train, y_train, X_test, y_test 已在此處準備好）...model = Sequential()
# 隱藏層1
model.add(Dense(1024, input_dim=41, activation='relu'))
model.add(Dropout(0.01))
# 隱藏層2
model.add(Dense(768, activation='relu'))
model.add(Dropout(0.01))
# 隱藏層3
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.01))
# 隱藏層4
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.01))
# 隱藏層5
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.01))
# 輸出層
model.add(Dense(1))
model.add(Activation('sigmoid'))model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# ...（訓練時的model.fit調用）...

觀察：

• 注意Dense和Dropout層的序列，每層的神經元數量比前一層少。這是一種常見的模式，逐步精煉特征。
• 輸出層和編譯（binary_crossentropy、sigmoid）保持不變，因為它仍然是二分類任務。

3. 多分類DNN（1個隱藏層）

最后，我們來看KDDCup 99/dnn/multiclass/dnn1.py。它使用與簡單二分類DNN相同的網絡結構，但適應了多分類：

# 來自 KDDCup 99/dnn/multiclass/dnn1.py（簡化版）
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.utils.np_utils import to_categorical # 用于標簽準備# ...（X_train, y_train1, X_test, y_test1 已在此處準備好）...
# 數據準備：對多分類標簽進行one-hot編碼
y_train = to_categorical(y_train1)
y_test = to_categorical(y_test1)model = Sequential()
# 隱藏層1
model.add(Dense(1024, input_dim=41, activation='relu'))
model.add(Dropout(0.01))
# 輸出層（N個神經元對應N個類別，softmax激活）
# 假設5個類別（正常、DoS、Probe、R2L、U2R）
model.add(Dense(5)) # 5個神經元對應5個類別
model.add(Activation('softmax'))model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# ...（訓練時的model.fit調用）...

觀察：

• y_train和y_test標簽在輸入模型前使用to_categorical（one-hot編碼）轉換，如第1章所述。
• 輸出層使用Dense(5)（5個類別）和Activation('softmax')。
• 損失函數現在是categorical_crossentropy，適用于one-hot編碼標簽。

這些示例清楚地展示了堆疊Dense和Dropout層的概念構成了DNN的核心，而輸出層和損失函數則根據具體分類任務（二分類 vs. 多分類）進行調整。

結論

現在，我們已經邁出了進入深度學習世界的第一步，探索了深度前饋神經網絡（DNN）！我們了解到，DNN通過其多個Dense隱藏層和relu激活函數，可以學習網絡流量數據中高度復雜的非線性模式。我們還看到了Dropout層在防止過擬合中的關鍵作用。

我們學習了如何使用Keras構建這些強大的模型，配置其輸入層、隱藏層和輸出層，并為二分類和多分類入侵檢測任務設置正確的loss函數，這些建立在前面章節的基礎上。

雖然DNN是經典模型的重大升級，但它們只是神經網絡的一種類型。在下一章中，我們將探索卷積神經網絡（CNN），它們特別擅長在具有空間或網格結構的數據中發現模式，盡管我們的網絡數據不是圖像，但它們有一種獨特的方式來檢測局部模式。

第5章：純卷積神經網絡（CNN）模型