1. 引言
在工業界廣泛使用的 Plonk SNARK 協議高度依賴 NTT 來完成計算。HyperPlonk 是 Plonk 的一個變種,它試圖通過用 Sumcheck 替代 NTT(以及其它改進)來提升并行性。Ingonyama團隊認為:
- Sumcheck 在 HyperPlonk 中所謂的并行化優勢可能被高估了。其根本問題在于:
- Sumcheck 的主要瓶頸并不在于計算,而是 內存訪問。
本文從硬件角度來討論 2023年論文HyperPlonk: Plonk with Linear-Time Prover and High-Degree Custom Gates,重點關注 HyperPlonk 的硬件友好性:
- 主要關注其核心構件 —— Multivariate多變量 SumCheck 協議,并將其 計算與內存復雜度 和 NTT(Number Theoretic Transform,數論變換)進行比較。
- 指出 Sumcheck 的性能瓶頸并非源于純粹的計算量,而是源于 內存訪問模式。這是一個關鍵性的區分:
- 理想情況下,像 Sumcheck 這樣的密碼學協議應該是 計算受限(compute-bound) 的,而不是 內存受限(memory-bound) 的。
- 因為現代硬件——尤其是 GPU 和專用加速器——在高吞吐量算術運算方面高度優化,但在受制于內存帶寬時卻往往表現不佳。
這種 內存受限行為 在 數論變換(NTT) 的使用中尤為明顯。NTT 是 Sumcheck 中多項式運算的基本構件。雖然 NTT 具有高度并行化的潛力,但它需要頻繁且結構化地訪問大量域元素數組,這對 內存子系統和緩存層次結構 帶來了巨大的壓力。結果是,即便底層的算術運算相對便宜,內存訪問開銷 仍可能主導整體性能。
要解決這一局限,需要:
- 優化 內存布局
- 采用 硬件感知的調度策略,
- 并在系統設計層面重新思考,從而推動硬件發揮其 計算極限,而不是被 內存天花板 所限制。
本文通過對 ICICLE(https://github.com/ingonyama-zk/icicle) 中 Sumcheck 實現的 性能剖析,提供了確鑿的證據,證明內存訪問確實是主要瓶頸,并提出了可為未來的 Sumcheck 及類似協議優化與硬件加速提供參考的見解。
本文只關注了 “標準 SumCheck” 的結構,而沒有討論其可能的改進空間。與 NTT 相比,SumCheck 的硬件加速問題幾乎沒有被深入研究過。很可能已經存在,或未來會出現一些方法來提升 SumCheck 的硬件友好性:
- 密碼學層面 —— 如 Fiat-Shamir 在其中的作用
- SumCheck 新變種
- 協議設計高層次的并行化思路 ——(其中一些已經在 HyperPlonk 論文中提出,比如批處理 Batching)
2. 背景 - HyperPlonk
Plonk 是業界最廣泛應用的 SNARK 之一。在標準的 Plonk 中,經過算術化(arithmetization)后,得到的執行軌跡會被插值為單變量多項式,因此協議大量依賴 NTT。
HyperPlonk 是 Plonk 的一種新變體,它將執行軌跡插值在 boolean hypercube(布爾超立方體)上,因此其執行軌跡的多項式表示是一個多變量多項式,并且在每個變量上的階數都是 1。這種表示被稱為 MLE(MultiLinear Extension,多線性擴展)。關于 HyperPlonk 的一個很好的綜述,可以參考 Benedikt Bunz 2022年10月在 ZKSummit8 的演講ZK8: Hyperplonk: PLONK without FFTs and with high degree gates - Benedikt Bünz 。
HyperPlonk 的一個關鍵優勢是:
- 消除了大規模 NTT,
而大規模 NTT 是 Plonk 在大電路中最大的計算瓶頸。通過轉移到布爾超立方體,不再需要單變量多項式。相反,HyperPlonk 依賴于多變量多項式運算。在 HyperPlonk 論文的第 3 節中,作者專門開發了一套處理多變量多項式的工具箱。下圖(取自論文)展示了 HyperPlonk 是如何基于這套工具箱構建的。可以看到,在最底層,核心就是經典的 SumCheck 協議,它必然會成為 HyperPlonk 的主要計算難點(忽略多項式承諾部分),完全替代了 NTT。
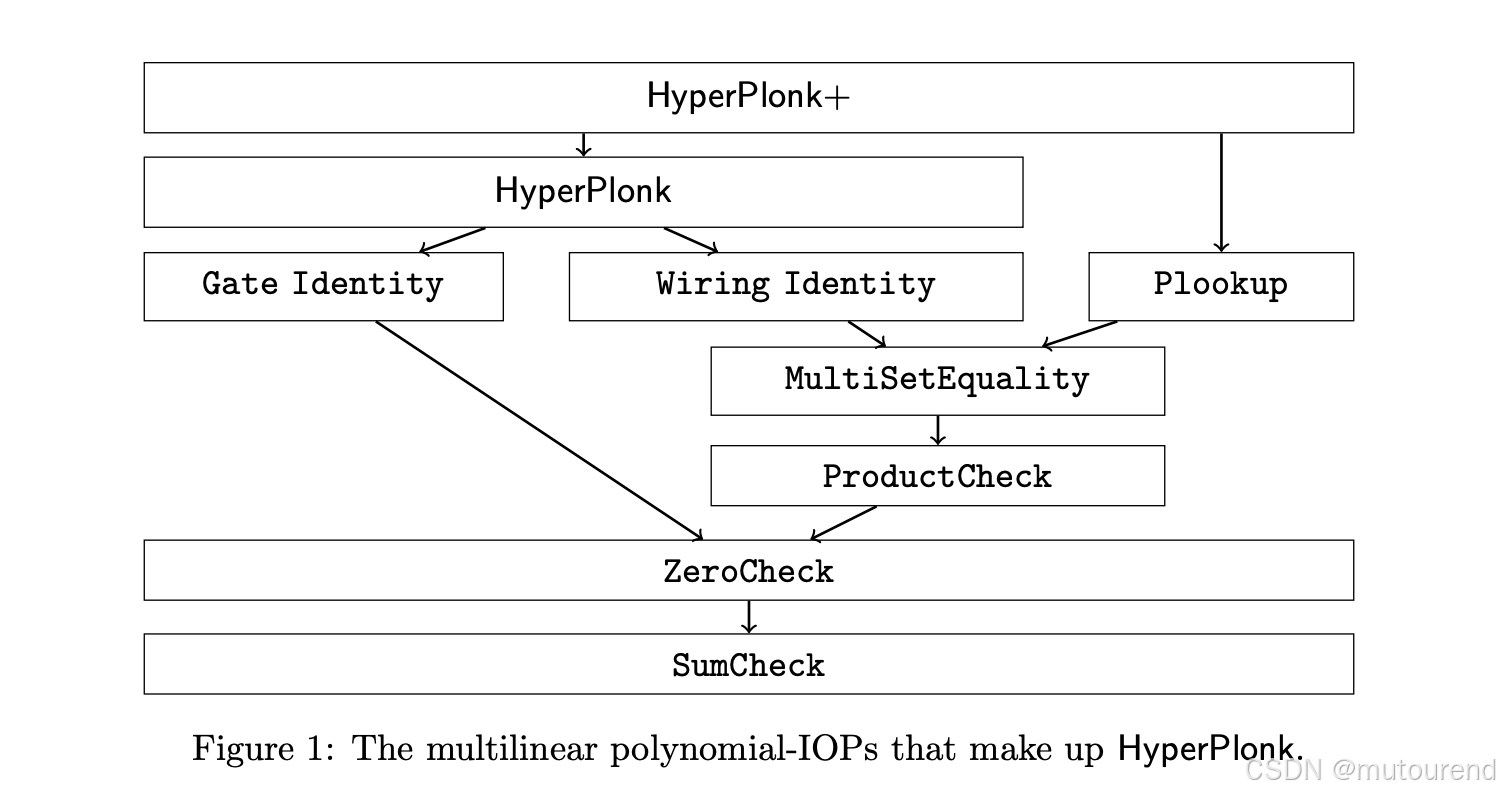
3. HyperPlonk 中的 SumCheck
3.1 HyperPlonk 中的 SumCheck 簡單示例
考慮一個展開為向量形式的執行軌跡。用長度為 8 的向量來說明這個想法,該向量由多項式的取值組成:
{fi}i=07,fi∈F.\{ f_i \}_{i=0}^7, \quad f_i \in \mathbb{F}. {fi?}i=07?,fi?∈F.
用多變量多項式 F(X3,X2,X1)F(X_3,X_2,X_1)F(X3?,X2?,X1?) 來插值這些值,如下表所示:
| f0f_0f0? | f1f_1f1? | f2f_2f2? | f3f_3f3? | f4f_4f4? | f5f_5f5? | f6f_6f6? | f7f_7f7? |
|---|---|---|---|---|---|---|---|
| F(0,0,0)F(0,0,0)F(0,0,0) | F(0,0,1)F(0,0,1)F(0,0,1) | F(0,1,0)F(0,1,0)F(0,1,0) | F(0,1,1)F(0,1,1)F(0,1,1) | F(1,0,0)F(1,0,0)F(1,0,0) | F(1,0,1)F(1,0,1)F(1,0,1) | F(1,1,0)F(1,1,0)F(1,1,0) | F(1,1,1)F(1,1,1)F(1,1,1) |
第一行是有限域元素,第二行表示插值的對應關系。用拉格朗日插值來表達:
F(X3,X2,X1)=f0(1?X3)(1?X2)(1?X1)+f1(1?X3)(1?X2)X1+f2(1?X3)X2(1?X1)+f3(1?X3)X2X1+f4X3(1?X2)(1?X1)+f5X3(1?X2)X1+f6X3X2(1?X1)+f7X3X2X1\begin{aligned} F(X_3,X_2,X_1) &= f_0(1-X_3)(1-X_2)(1-X_1) + f_1(1-X_3)(1-X_2)X_1 \\ &\quad + f_2(1-X_3)X_2(1-X_1) + f_3(1-X_3)X_2X_1 \\ &\quad + f_4X_3(1-X_2)(1-X_1) + f_5X_3(1-X_2)X_1 \\ &\quad + f_6X_3X_2(1-X_1) + f_7X_3X_2X_1 \end{aligned} F(X3?,X2?,X1?)?=f0?(1?X3?)(1?X2?)(1?X1?)+f1?(1?X3?)(1?X2?)X1?+f2?(1?X3?)X2?(1?X1?)+f3?(1?X3?)X2?X1?+f4?X3?(1?X2?)(1?X1?)+f5?X3?(1?X2?)X1?+f6?X3?X2?(1?X1?)+f7?X3?X2?X1??
其中,XXX 和 1?X1-X1?X 是定義在二元域上的Lagrange base polynomial(拉格朗日基多項式)。這個唯一的多項式 F(X3,X2,X1)F(X_3,X_2,X_1)F(X3?,X2?,X1?) 被稱為 向量的多線性擴展(MLE)。
在該例子中,SumCheck 問題定義如下:
∑Xi∈{0,1}F(X3,X2,X1)=?C,C∈F.\sum_{X_i\in \{0,1\}} F(X_3,X_2,X_1) \stackrel{?}{=} C, \quad C \in \mathbb{F}. Xi?∈{0,1}∑?F(X3?,X2?,X1?)=?C,C∈F.
該協議的流程如下:在每一輪中,證明者計算并承諾一個單變量(線性)多項式,并接收來自驗證者的隨機挑戰。
| 輪次 | 證明者 P\mathcal{P}P | 通信 | 驗證者 V\mathcal{V}V |
|---|---|---|---|
| 1 | r1(X):=∑X2,3∈{0,1}F(X3,X2,X)r_1(X) := \sum_{X_{2,3}\in \{0,1\}} F(X_3, X_2,X)r1?(X):=∑X2,3?∈{0,1}?F(X3?,X2?,X) | r1(X)??α1∈Fr_1(X)\longrightarrow\\\longleftarrow \alpha_1\in \mathbb{F}r1?(X)??α1?∈F | C=?∑X∈{0,1}r1(X)C\stackrel{?}{=} \sum_{X\in\{0,1\}} r_1(X)C=?∑X∈{0,1}?r1?(X) |
| 2 | r2(X):=∑X3∈{0,1}F(X3,X,α1)r_2(X) := \sum_{X_3\in \{0,1\}} F(X_3, X,\alpha_1)r2?(X):=∑X3?∈{0,1}?F(X3?,X,α1?) | r2(X)??α2∈Fr_2(X)\longrightarrow\\\longleftarrow \alpha_2\in \mathbb{F}r2?(X)??α2?∈F | r1(α1)=?∑X∈{0,1}r2(X)r_1(\alpha_1)\stackrel{?}{=} \sum_{X\in\{0,1\}} r_2(X)r1?(α1?)=?∑X∈{0,1}?r2?(X) |
| 3 | r3(X):=F(X,α2,α1)r_3(X) := F(X, \alpha_2,\alpha_1)r3?(X):=F(X,α2?,α1?) | r3(X)?r_3(X)\longrightarrowr3?(X)? | r2(α2)=?∑X∈{0,1}r3(X)r3(α3)=?F(α3,α2,α1)r_2(\alpha_2)\stackrel{?}{=} \sum_{X\in\{0,1\}} r_3(X)\\r_3(\alpha_3)\stackrel{?}{=} F(\alpha_3,\alpha_2,\alpha_1)r2?(α2?)=?∑X∈{0,1}?r3?(X)r3?(α3?)=?F(α3?,α2?,α1?) |
在此希望估計證明者在每輪計算這些多項式時的復雜度。注意,證明者承諾每個線性單變量多項式的過程并不是計算瓶頸,因為它只涉及簡單的橢圓曲線加法或一個小規模的 MSM。
經過簡單計算可得,第 1 輪后的多項式形式為:
r1(X)=∑Xi∈{0,1}F(X2,X2,X)=∑i=03r1(i)(X),r1(i)(X)=f2i(1?X)+f2i+1Xr_1(X) = \sum_{X_i \in \{0,1\}} F(X_2,X_2,X) = \sum_{i=0}^3 r_1^{(i)}(X), \quad r_1^{(i)}(X) = f_{2i}(1-X) + f_{2i+1}X r1?(X)=Xi?∈{0,1}∑?F(X2?,X2?,X)=i=0∑3?r1(i)?(X),r1(i)?(X)=f2i?(1?X)+f2i+1?X
顯然:
∑X∈{0,1}r1(X)=r1(0)+r1(1)=∑i=03(f2i+f2i+1)=C\sum_{X \in \{0,1\}} r_1(X) = r_1(0) + r_1(1) = \sum_{i=0}^3 (f_{2i} + f_{2i+1}) = C X∈{0,1}∑?r1?(X)=r1?(0)+r1?(1)=i=0∑3?(f2i?+f2i+1?)=C
設第 1 輪的挑戰為 α1∈Fp\alpha_1 \in \mathbb{F}_pα1?∈Fp?。那么第 2 輪的多項式為:
r2(X)=∑Xi∈{0,1}F(X2,X,α1)=∑i=01r2(i)(X),r2(i)(X)=r1(2i)(α1)(1?X)+r1(2i+1)(α1)Xr_2(X) = \sum_{X_i \in \{0,1\}} F(X_2,X,\alpha_1) = \sum_{i=0}^1 r_2^{(i)}(X), \quad r_2^{(i)}(X) = r_1^{(2i)}(\alpha_1)(1-X) + r_1^{(2i+1)}(\alpha_1)X r2?(X)=Xi?∈{0,1}∑?F(X2?,X,α1?)=i=0∑1?r2(i)?(X),r2(i)?(X)=r1(2i)?(α1?)(1?X)+r1(2i+1)?(α1?)X
類似地,設第 2 輪的挑戰為 α2∈Fp\alpha_2 \in \mathbb{F}_pα2?∈Fp?。則第 3 輪的多項式為:
r3(X)=F(X,α2,α1)=r2(0)(α2)(1?X)+r2(1)(α2)Xr_3(X) = F(X,\alpha_2,\alpha_1) = r_2^{(0)}(\alpha_2)(1-X) + r_2^{(1)}(\alpha_2)X r3?(X)=F(X,α2?,α1?)=r2(0)?(α2?)(1?X)+r2(1)?(α2?)X
證明者的算法可以用下圖表示:
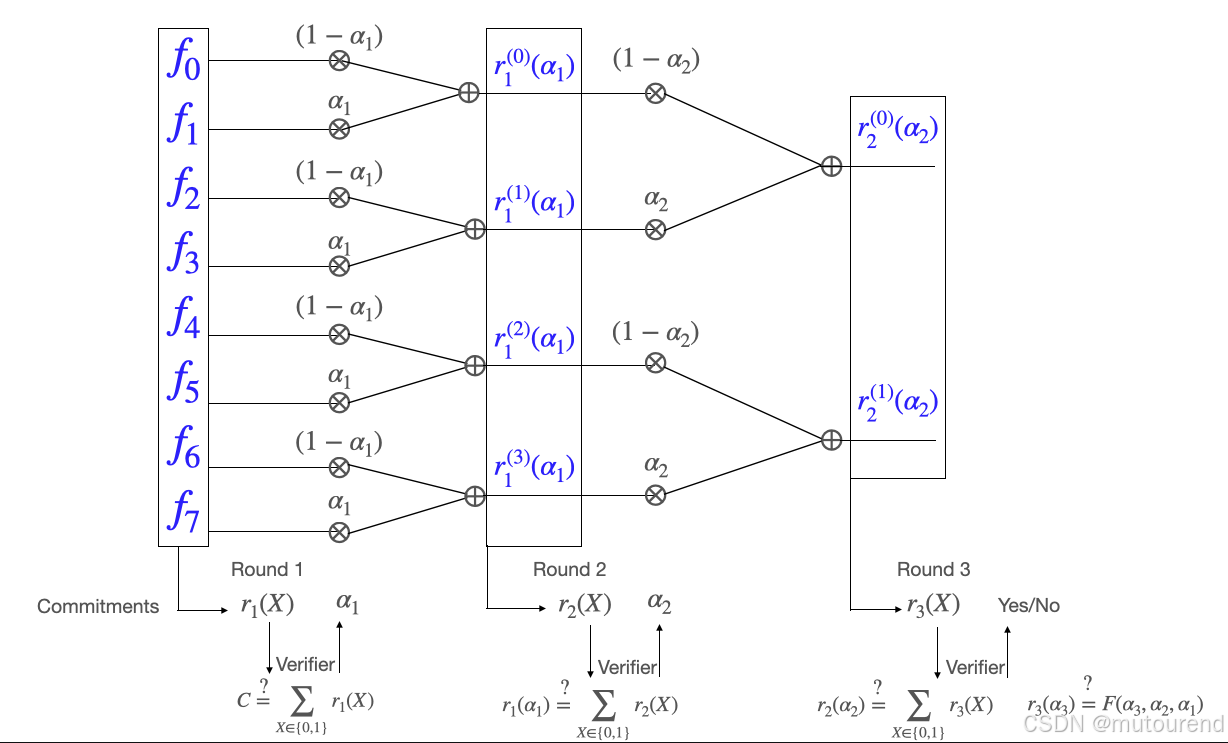
證明者的復雜度總結如下表(記號 xFx\mathbb{F}xF 表示內存中存有 xxx 個有限域元素):
| 輪次 | 操作 | 內存 | 乘法數 | 加法數 |
|---|---|---|---|---|
| 預處理 | 存儲 fi,?i=0,1,…,7f_i, \forall i=0,1,\dots,7fi?,?i=0,1,…,7 | 8F8\mathbb{F}8F | - | - |
| 1 | 讀取 fi,?i=0,1,…,7f_i, \forall i=0,1,\dots,7fi?,?i=0,1,…,7,承諾 r1(X)r_1(X)r1?(X),接收 α1\alpha_1α1? | |||
| 讀取 fi,?i=0,1,…,7f_i, \forall i=0,1,\dots,7fi?,?i=0,1,…,7,計算 r1(i)(α1),?i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3r1(i)?(α1?),?i=0,1,2,3 | - | 8 | 4 | |
| 清除 fi,?i=0,1,…,7f_i, \forall i=0,1,\dots,7fi?,?i=0,1,…,7,存儲 r1(i)(α1),?i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3r1(i)?(α1?),?i=0,1,2,3 | 4F4\mathbb{F}4F | - | - | |
| 2 | 讀取 r1(i)(α1),?i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3r1(i)?(α1?),?i=0,1,2,3,承諾 r2(X)r_2(X)r2?(X),接收 α2\alpha_2α2? | |||
| 讀取 r1(i)(α1),?i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3r1(i)?(α1?),?i=0,1,2,3,計算 r2(i)(α2),?i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1r2(i)?(α2?),?i=0,1 | - | 4 | 2 | |
| 清除 r1(i)(α1),?i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3r1(i)?(α1?),?i=0,1,2,3,存儲 r2(i)(α2),?i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1r2(i)?(α2?),?i=0,1 | 2F2\mathbb{F}2F | - | - | |
| 3 | 讀取 r2(i)(α2),?i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1r2(i)?(α2?),?i=0,1,承諾 r3(X)r_3(X)r3?(X) | |||
| 清除 r2(i)(α2),?i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1r2(i)?(α2?),?i=0,1 |
3.2 HyperPlonk 中的 SumCheck 一般形式
該算法的一般形式可以很容易地從上面的簡單例子推廣出來。考慮一個大小為 T=2nT = 2^nT=2n 的執行軌跡(為方便起見,假設該執行軌跡總是補零到 2 的冪)。該執行軌跡可以用一個多變量多項式 F(Xn,…,X1)F(X_n, \ldots, X_1)F(Xn?,…,X1?) 進行插值。證明者算法如下:
-
第 1 輪,證明者計算線性多項式:
r1(i)(X)=(1?X)f2i+Xf2i+1,?i=0,…,T/2?1r_1^{(i)}(X) = (1-X) f_{2i} + X f_{2i+1}, \quad \forall i=0, \ldots, T/2-1 r1(i)?(X)=(1?X)f2i?+Xf2i+1?,?i=0,…,T/2?1
并承諾它們的和:
r1(X)=∑i=0T/2?1r1(i)(X)=∑X∈{0,1}F(Xn,…,X2,X)r_1(X) = \sum_{i=0}^{T/2-1} r_1^{(i)}(X) = \sum_{X \in \{0,1\}} F(X_n, \ldots, X_2, X) r1?(X)=i=0∑T/2?1?r1(i)?(X)=X∈{0,1}∑?F(Xn?,…,X2?,X)
然后,證明者接收驗證者給出的挑戰 α1\alpha_1α1?。 -
第 kkk 輪,證明者計算線性多項式:
rk(i)(X)=(1?X)rk?1(2i)(αk?1)+Xrk?1(2i+1)(αk?1),?i=0,…,T/2k?1r_k^{(i)}(X) = (1-X) r_{k-1}^{(2i)}(\alpha_{k-1}) + X r_{k-1}^{(2i+1)}(\alpha_{k-1}), \quad \forall i=0, \ldots, T/2^k - 1 rk(i)?(X)=(1?X)rk?1(2i)?(αk?1?)+Xrk?1(2i+1)?(αk?1?),?i=0,…,T/2k?1
并承諾它們的和:
rk(X)=∑i=0T/2k?1rk(i)(X)=∑X∈{0,1}F(Xn,…,Xk+1,X,αk?1,…,α1)r_k(X) = \sum_{i=0}^{T/2^k-1} r_k^{(i)}(X) = \sum_{X \in \{0,1\}} F(X_n, \ldots, X_{k+1}, X, \alpha_{k-1}, \ldots, \alpha_1) rk?(X)=i=0∑T/2k?1?rk(i)?(X)=X∈{0,1}∑?F(Xn?,…,Xk+1?,X,αk?1?,…,α1?)
然后,證明者接收驗證者給出的挑戰 αk\alpha_kαk?。 -
最終第 nnn 輪,證明者計算并承諾線性多項式:
rn(X)=(1?X)rn?1(0)(αn?1)+Xrn?1(1)(αn?1)r_n(X) = (1-X) r_{n-1}^{(0)}(\alpha_{n-1}) + X r_{n-1}^{(1)}(\alpha_{n-1}) rn?(X)=(1?X)rn?1(0)?(αn?1?)+Xrn?1(1)?(αn?1?)
因此,證明者的總體復雜度為:
- 2T?42T-42T?4 次乘法
- T?2T-2T?2 次加法
- 以及存儲 TTT 個有限域元素的內存
事實上,可以進一步優化:
rk(i)(X)=(1?X)rk?1(2i)(αk?1)+Xrk?1(2i+1)(αk?1)=rk?1(2i)(αk?1)+X(rk?1(2i+1)(αk?1)?rk?1(2i)(αk?1))r_k^{(i)}(X) = (1-X) r_{k-1}^{(2i)}(\alpha_{k-1}) + X r_{k-1}^{(2i+1)}(\alpha_{k-1}) = r_{k-1}^{(2i)}(\alpha_{k-1}) + X \big(r_{k-1}^{(2i+1)}(\alpha_{k-1}) - r_{k-1}^{(2i)}(\alpha_{k-1})\big) rk(i)?(X)=(1?X)rk?1(2i)?(αk?1?)+Xrk?1(2i+1)?(αk?1?)=rk?1(2i)?(αk?1?)+X(rk?1(2i+1)?(αk?1?)?rk?1(2i)?(αk?1?))
這樣可以將所需的乘法次數減半。
更一般地來說:
Sumcheck 協議 通常用于證明一個關于多項式在多維域上求和的斷言(通常是布爾超立方體 {0,1}d\{0,1\}^d{0,1}d)。換句話說,證明者希望讓驗證者相信:
- 給定多項式 P(x1,x2,…,xd)P(x_1, x_2, …, x_d)P(x1?,x2?,…,xd?),在所有變量取值的情況下,其求和結果等于某個特定值 CCC。
形式化表示為:
∑x1,x2,…,xd∈FP(x1,x2,…,xd)=C\sum_{x_1,x_2,\ldots,x_d \in \mathbb{F}} P(x_1, x_2, \ldots, x_d) = C x1?,x2?,…,xd?∈F∑?P(x1?,x2?,…,xd?)=C
Sumcheck 協議是一個迭代過程,每一輪(iteration)包含兩個主要計算:
- 1)累積當前輪次的多項式;
- 2)通過“折疊(folding)”多項式,使元素數量減少一半。
在每一輪中,驗證者會生成挑戰值,用來折疊多項式。
4. 引入 Fiat-Shamir
Fiat-Shamir 變換可以將交互式的public coin proof(如 SumCheck 協議)轉換為非交互式證明。
在該變換中,挑戰 αi\alpha_iαi? 并不是由驗證者發送,而是在每一輪通過計算前一輪協議的通信記錄(transcript)的哈希函數來生成。
為了避免安全漏洞,每個哈希函數的輸入必須包含前一輪的所有可驗證結果。相關的漏洞分析見:
- 2022年4月博客 Coordinated disclosure of vulnerabilities affecting Girault, Bulletproofs, and PlonK
- 和 更技術化的說明見2016年論文 How not to Prove Yourself: Pitfalls of the Fiat-Shamir Heuristic and Applications to Helios。
因此,在 SumCheck 協議中,每一輪必須 順序執行,而不能并行化跨輪次的計算。正如下文所示,這一事實嚴重限制了在 HyperPlonk 中進行并行計算的能力。
5. 硬件中的 SumCheck
基于上文對非交互式 SumCheck 的介紹,可以總結出每一輪 iii 的操作模式如下:
- (從內存中)讀取 2i2^i2i 個元素
- 計算 ai=hash(transcript)a_i = \text{hash(transcript)}ai?=hash(transcript)
- 計算新的 2i?12^{i-1}2i?1 個元素
- 寫入 2i?12^{i-1}2i?1 個元素(到內存中)
具體來說,假設有 2302^{30}230 個有限域元素。為了進入下一輪——得到 2292^{29}229 個元素,必須使用(從內存中讀取)全部的 2302^{30}230 個元素。在完成這一步之前,不能繼續進入再下一輪——即 2282^{28}228 個元素的階段。
這種 “硬停頓(hard stop)” 意味著在每一輪中,都必須重新訪問內存。舉個例子,對于大小 2302^{30}230 的 SumCheck,必須對內存進行 30 次讀寫。
對于足夠小的規模,如 2182^{18}218,這些數據可以存儲在 SRAM 中。SRAM 速度很快,幾乎不會成為瓶頸。
然而,對于大規模的 SumCheck,如 2302^{30}230(這也是在實際中預期會遇到的規模),部分輪次必須使用 DRAM(如 DDR 或 HBM)。而 DRAM 的速度很慢,會成為瓶頸,甚至超過 SumCheck 計算本身的開銷。
下圖展示了這種 SumCheck 的數據流:
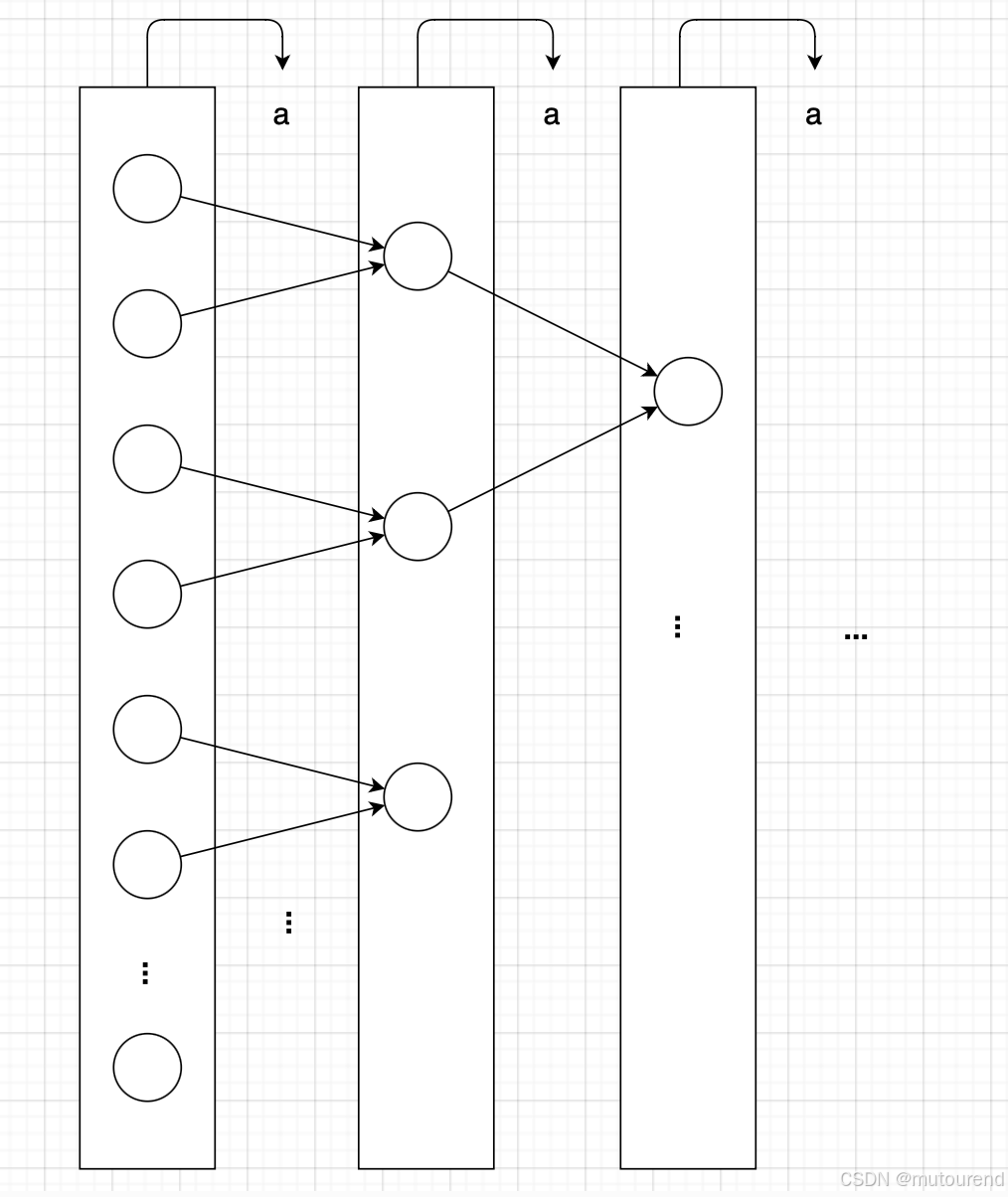
類似這樣的 內存瓶頸 正是在設計硬件加速器時通常希望避免的,因為這類計算幾乎沒有辦法通過硬件加速來優化。由于其本質,標準的 SumCheck 輪次結構極度 串行化,因此幾乎沒有并行加速的空間。
5.1 硬件中的 NTT
最明顯的對比就是 NTT 在硬件中的實現方式。本文不會像討論 SumCheck 那樣深入分析 NTT。為了對比,給出以下示意圖:
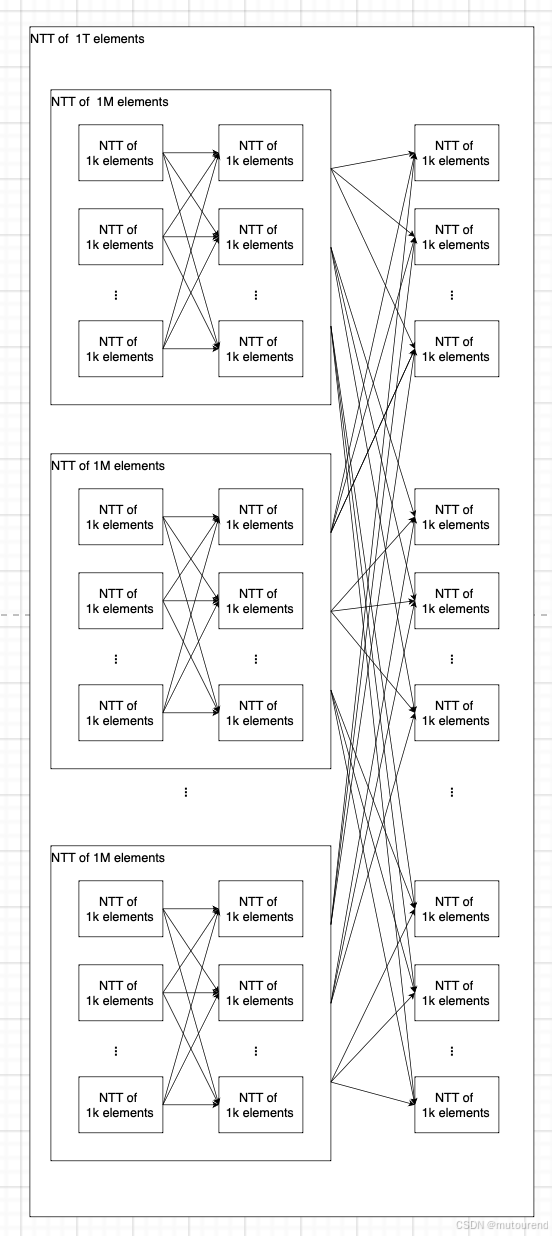
NTT 天然具有較強的 并行性,因此多個輪次可以在 不返回內存 的情況下連續進行。注意:
- 在 NTT 中,由于沒有 Fiat-Shamir 變換的約束,因此不存在 硬停頓(hard stop) —— 一輪計算的輸出(部分結果)可以直接作為下一輪計算的輸入(部分輸入)。
經驗法則是:
- 可以在 僅一次內存訪問 的情況下完成一個規模為 1k1k1k 個元素的完整 NTT。這比 SumCheck 快 10 倍!
如:甚至可以用 僅 3 次內存讀寫(讀取并寫回所有元素)完成一個 規模為 1 萬億 個元素的 NTT。
這使得 NTT 是計算受限(compute-bound)的,而不是 內存受限(memory-bound)的。
事實上,Ingonyama團隊在 GPU 和 FPGA 上的 NTT 實現已經將計算速度提升到這樣一個程度:
- 在所有相關規模下,計算本身都不再是瓶頸!
這些實現所面臨的下一個瓶頸是 PCIe 帶寬,也就是與主機進行通信時的傳輸速度。
5.2 Ingonyama團隊 ICICLE 中的 Sumcheck
Ingonyama團隊 在 CPU 和 GPU(CUDA 和 Metal)上的 Sumcheck 實現,首次在 ICICLE V3.5 中引入,利用 Fiat-Shamir 啟發式將協議轉化為非交互形式,從而消除了基于輪次的通信需求。
除了支持一組固定的運算外,這些實現還允許通過一種稱為 Program 類的高級抽象來定義多線性多項式的用戶自定義積。該類使開發者能夠在向量上定義自定義逐元素的 lambda 函數,然后將其編譯為針對目標硬件優化的后端代碼。ICICLE V3.5 隨附了內置程序,如:
- A(X)?B(X)?C(X)A(X) * B(X) - C(X)A(X)?B(X)?C(X)
- eq(X)?(A(X)?B(X)?C(X))\text{eq}(X) * (A(X) * B(X) - C(X))eq(X)?(A(X)?B(X)?C(X))
同時仍然保留了指定更復雜約束的完全靈活性。系統設計時注重硬件無關的優化,利用 CPU 的多線程和 GPU 的并行性來最小化內存開銷并最大化算術吞吐量。這些改進是 ICICLE 為使密碼學原語在不同架構上既可移植又高效的更廣泛努力的一部分。
CUDA 實現的計算輪次結構略有不同。在每一輪中,它同時計算上一輪的折疊結果和當前輪的多項式評估,從而消除了不必要的內存訪問。值得注意的是,在第一輪中,僅進行多項式評估而不執行折疊。這種設計帶來了目前所知最節省內存的實現方式,僅執行折疊嚴格所需的內存操作。
Fiat-Shamir 挑戰和多項式累積直接在設備上計算,無需在每一輪后將數據傳回主機再傳回設備。這避免了昂貴的往返數據傳輸,提高了整體吞吐量。
Ingonyama團隊 將使用該實現來驗證此前提出的觀點:
- Sumcheck 是 受限于內存而非計算能力。
5.2.1 Sumcheck 的限制因素
Ingonyama團隊 使用 NVIDIA Nsight Compute 對 ICICLE 的 CUDA 實現進行性能剖析,并在 NVIDIA L4 GPU 上識別性能瓶頸。該剖析工具為每個 CUDA 內核提供詳細的指標,包括運行時間、內存帶寬和寄存器使用情況。為了確定協議的限制因素,Ingonyama團隊 重點關注內存和計算的 SoL(Speed of Light)吞吐量 指標。SoL 指標反映某個子單元的運行接近理論最大吞吐量的程度,有助于判斷瓶頸是由內存訪問還是計算引起的。
在此次實驗中,使用了 4 個大小為 2252^{25}225 的多項式(即 HyperPlonk 使用的規模范圍),并采用組合函數 EQ(AB-C)(R1CS zero check)。
下圖展示了 ICICLE Sumcheck 實現的主要 CUDA 內核在協議前 13 輪中的計算和內存 SoL 吞吐量,揭示了執行過程中的性能趨勢。
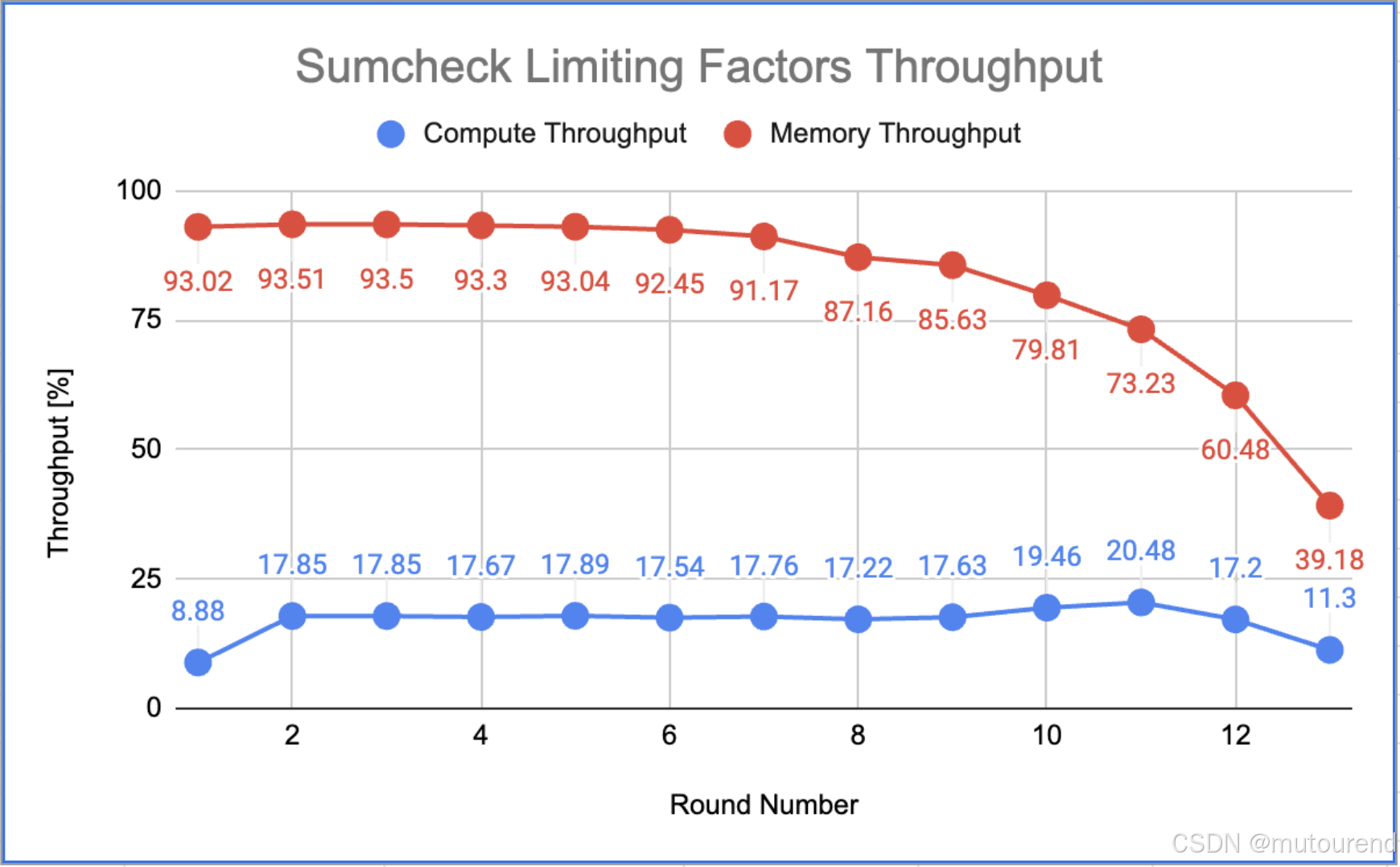
數據揭示了內存與計算吞吐量在初始階段的關系:
- 內存 SoL 吞吐量接近峰值,而計算 SoL 吞吐量相對較低。
當一個程序的內存吞吐受限,導致計算資源無法得到充分利用時,它就被認為是 內存受限(memory-bound)。從圖表可見,內存接近滿負荷運行,而計算資源未被充分利用,明顯表明存在內存瓶頸。
隨著輪次推進,出現了一個關鍵模式:
- 內存吞吐逐漸下降,而計算吞吐保持穩定甚至略有上升。
第一次到第二次輪次間計算吞吐的翻倍源于協議結構的特性。值得注意的是,只有當內存吞吐下降到 60% 以下時,計算吞吐才開始下降,這進一步強化了“內存是主要限制因素”的結論。下圖對此進行了說明:
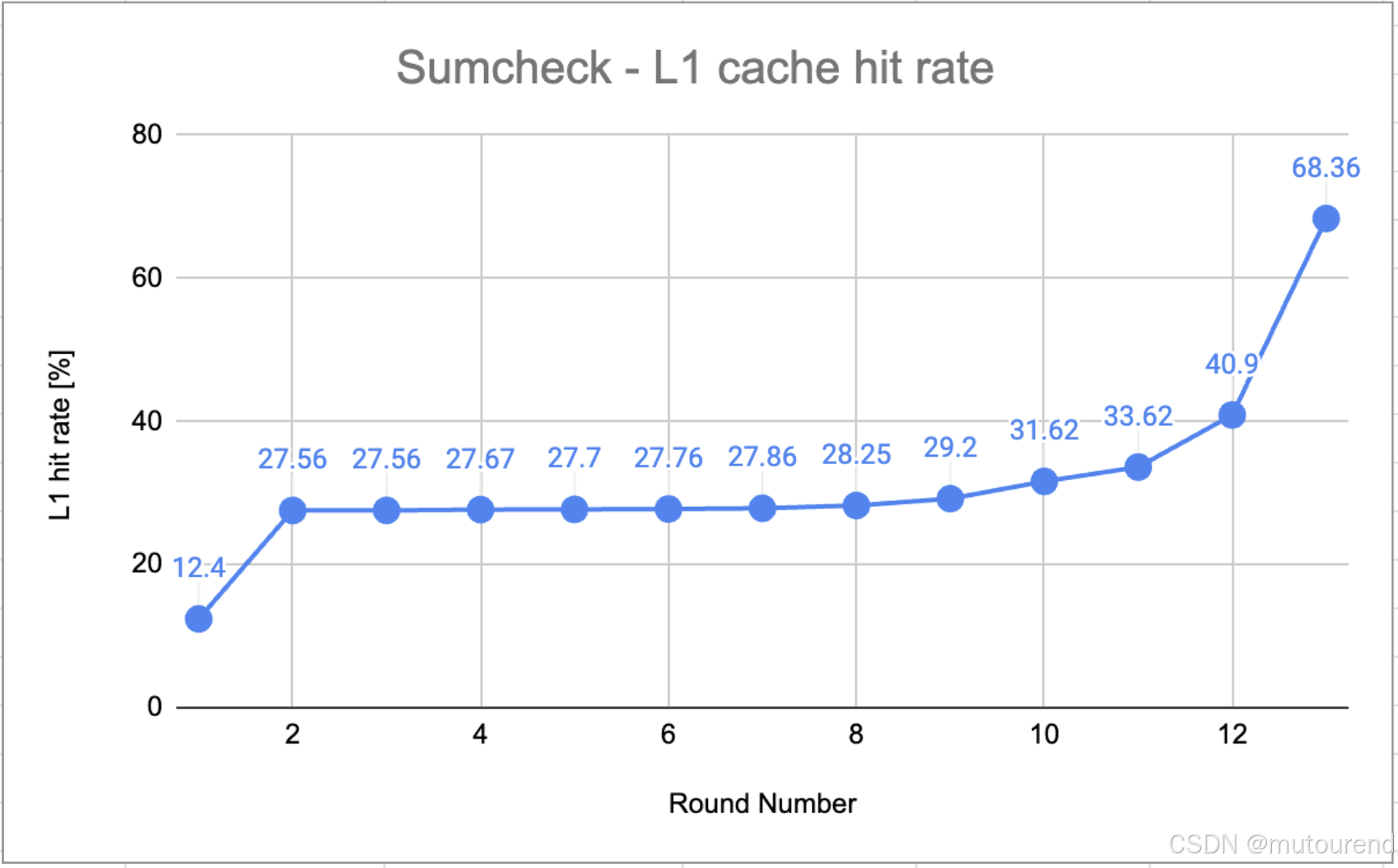
L1 緩存命中率隨著內存吞吐量的下降而上升。
隨著輪次推進,多項式規模縮小并逐漸能被緩存容納,緩存命中率上升。這樣一來,更多數據可以直接從緩存中訪問,而不必從較慢的主存中獲取,從而降低了內存吞吐。同時,計算吞吐因更快的數據訪問而提升。
計算利用率因更快的內存訪問而提高,這是程序 內存受限 的有力證據。
證據明確表明,內存訪問是系統的主要瓶頸。這一點得到了 持續較高的內存 SoL 吞吐量 和 較低的計算利用率 的支持,同時計算吞吐量和 L1 緩存命中率的表現也進一步印證了這一點:隨著輪次推進,內存利用率下降,計算性能卻有所提高——這進一步強化了工作負載是 內存受限 的結論。
換言之,系統的整體性能是 由內存訪問速度 限制的,而非由計算吞吐量所限制。
6. 結論
那么問題來了 —— 是繼續使用 Plonk + NTT 更好,還是采用 HyperPlonk + MLE-SumCheck 更好?
- 至少從 硬件角度 來看,盡管 NTT 本身并沒有非常強的并行性,但它依然比 MLE-SumCheck 更加 硬件友好。Ingonyama團隊注意到,相同的結構也出現在 FRI 中,如可以參考 plonky2 中的 FRI 實現https://github.com/0xPolygonZero/plonky2/blob/769175808448cecc7b431d7293e2d689af635a4b/plonky2/src/fri/prover.rs#L69。
Ingonyama團隊推測,之前之所以沒有太多人討論 FRI 的硬件加速問題,是因為在現有系統(如 STARKs)中,FRI 的開銷只占總體計算的一小部分,尤其是與大量、規模更大的 NTT 相比時。
Ingonyama團隊實證結果表明,Sumcheck 協議本質上是內存受限的——其性能更多受到內存訪問速度的制約,而非計算能力。
因此,優化工作應聚焦于提升內存效率,而不是單純提高計算性能。
針對內存優化,即使在計算資源有限的硬件上,也能為 Sumcheck 的實現帶來顯著的性能提升。
另外一個思考在于:
- 是否已經到了這樣一個階段 —— 零知識證明協議必須結合硬件來共同設計?
參考資料
[1] Ingonyama團隊2025年4月1日博客 Hardware-friendliness of HyperPlonk, Part2
[2] Ingonyama團隊2022年12月28日hackmd Hardware-friendliness of HyperPlonk
[3] Ingonyama團隊2025年4月1日hackmd Hardware-friendliness of HyperPlonk, Part2

手把手教你做)





與諧波分析)






)
)
詳解)


)