97. 小明逛公園

Floyd 算法

dijkstra,?bellman_ford 是求單個起點到單個終點的最短路徑，dijkstra無法解決負權邊的問題，?bellman_ford解決了負權邊的問題，但二者都是基于單起點和單終點。

而Floyd 算法旨在解決多個起點到多個終點的最短路徑問題，且Floyd 算法對邊的權值正負沒有要求，都可以處理。Floyd 算法采用的是動態規劃的思想，那涉及到動態規劃就需要用到動態規劃五部曲了。

• 1. dp定義

dp[i][j][k] 表示 節點i 到 節點j 以[1...k] 集合中的一個節點為中間節點的最短距離。

k 是指取?區間[1,k] 中的一個節點作為中間節點；節點i 到 節點j 的最短路徑中 一定是經過很多節點，那么這個集合用[1...k] 來表示。

• 2. dp初始化

剛開始進來時，每條邊的關系進來時都不需要經過中間節點，因此輸入的邊的關系用dp[i][j][0]進行初始化。

• 3. dp遞推公式

當到達節點k時，此時有兩種狀態，一種是經過節點k，另外一種是不經過中間節點k。

1. 經過節點k，那此時dp[i][j][k] = dp[i][k][k-1] + dp[k][j][k-1]
2. 不經過中間節點k，那此時dp[i][j][k] = dp[i][j][k-1]

求的是最小距離，因此dp[i][j][k] = min(?dp[i][j][k-1] + dp[k][j][k-1],?dp[i][j][k-1])

補充：節點1 到 節點9 的最短距離 是不是可以由 節點1 到節點5的最短距離 + 節點5到節點9的最短距離組成呢？即 grid[1][9] = grid[1][5] + grid[5][9]。

• 4. 遍歷順序

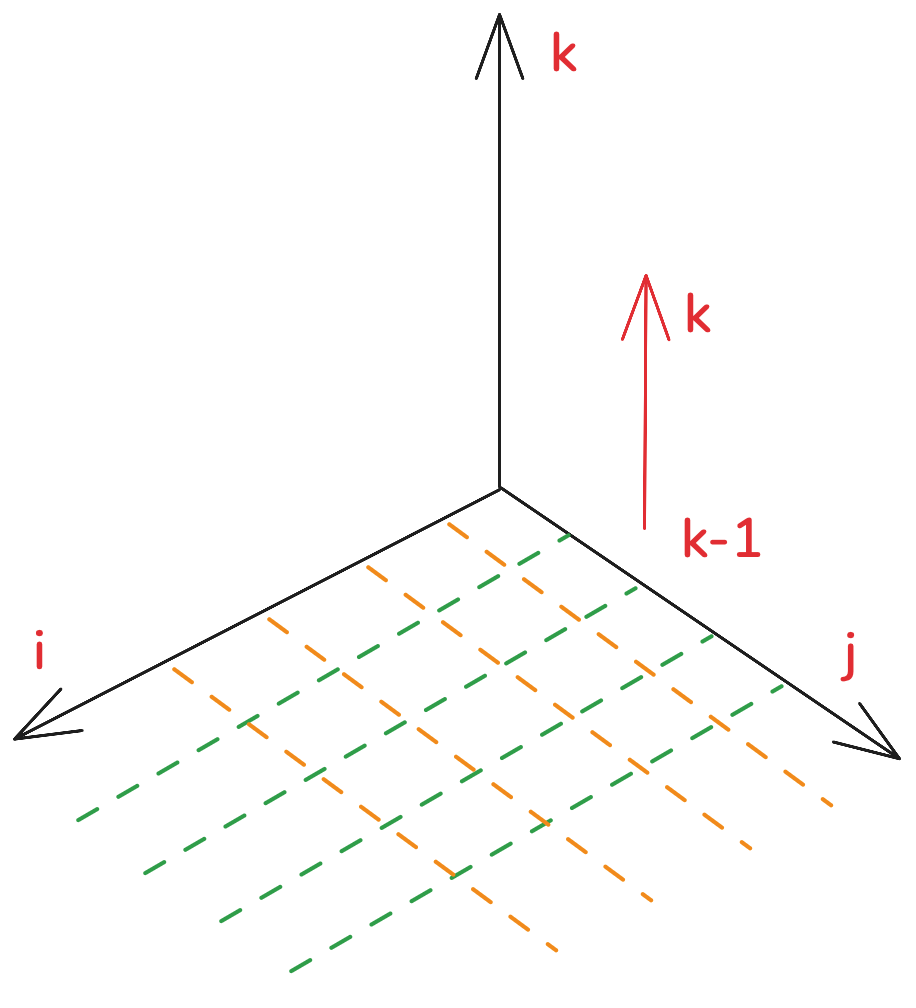
由于初始化得到的是一個平面，且遞推公式是往上去進行遞推的，因此需要三個循環去進行遞推，k處于外循環，i，j構成內循環。即先平面再高度的方式去進行遞推。

• 5. 打印dp

Code：

if __name__ == "__main__":scenery_size, road_size = map(int, input().split())length = scenery_size + 1# 1. dp數組定義dp = [ [[float('inf')]*length for _ in range(length)] for _ in range(length) ]     ##先構造一個二維數組，再外封遍歷從而構成三維數組# 2. dp初始化for _ in range(road_size):u, v, w = map(int, input().split())dp[u][v][0] = w         dp[v][u][0] = w         ## 無向圖Q = int(input())plan = []for _ in range(Q):start, end = map(int, input().split())plan.append([start,end])# 3. 遞推公式# dp[i][j][k] = min(dp[i][j][k-1], dp[i][k][k-1]+dp[k][j][k-1])# 4.遍歷順序for k in range(1, length):for i in range(1,length):for j in range(1,length):dp[i][j][k] = min(dp[i][j][k-1], dp[i][k][k-1]+dp[k][j][k-1])# 5. 打印dp數組for i in range(len(plan)):  ## 結果輸出start = plan[i][0]end = plan[i][1]if dp[start][end][scenery_size] != float('inf'):print(dp[start][end][scenery_size])else:print(-1)

其他：

• dp = [ [[float('inf')]*length for _ in range(length)] for _ in range(length) ]

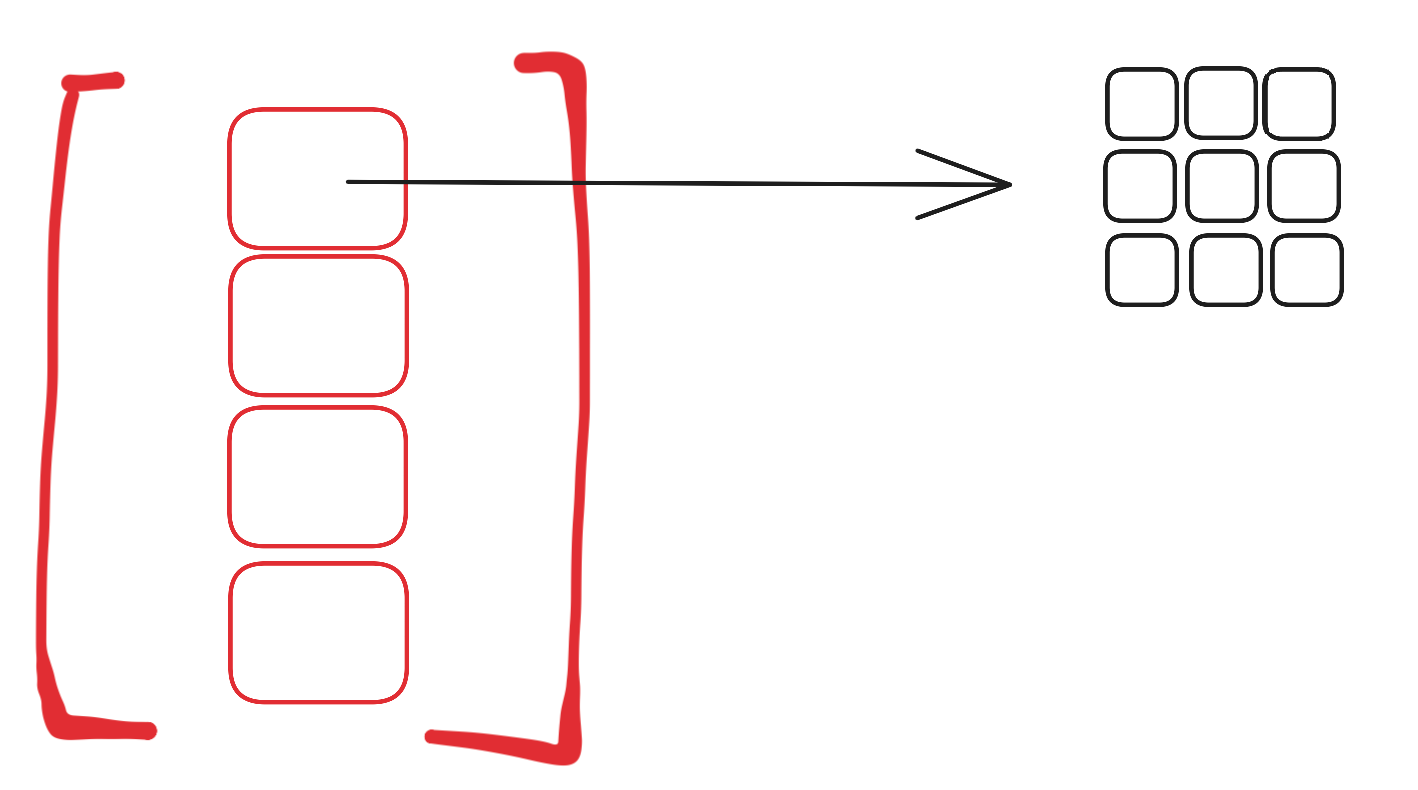
先構造 length 個list, 然后每個list里面存儲的是一個二維矩陣。

• Floyd的算法是基于點的角度去進行計算的，因此適合于稠密圖（邊多），不適合稀疏圖（邊少）。也就說當你圖中有1萬個點，但只有一條邊時，此時用這個算法就不合適。（計算時間復雜度O(n^3), n是節點數目）

127. 騎士的攻擊

A * 算法

關鍵：啟發式函數，來確定廣搜的方向。

A * 算法其實就是個改進版的廣搜，其與BFS的區別如下。BFS是每次都往四面八方去進行搜索，而A*會計算當前離終點的距離去判斷要往那個方向進行廣搜，從而極大減少了廣搜的次數。

由于每次BFS都是選取dis最小的一個元素進行下一次BFS，因此需要用到小頂堆。

dis = cur_dis + remaining_dis（通過引入這個變量來明確遍歷的方向）

• cur_dis: 表示從起點出發到當前節點時已走過的步數。（題目要求是輸出步數，而不是距離）
• remaining_dis：當前節點 到 終點的距離。
• dis 與?cur_dis ?呈正相關，當dis有最小時，此時cur_dis有最小。

如何計算、保存 cur_dis，并通過小頂堆對dis進行排序，通過堆頂元素來指導BFS的方向是這道題的關鍵。??

Code

from collections import deque
import heapq
import mathdirections = [[2,1],[-2,1],[1,2],[-1,2],[2,-1],[-2,-1],[1,-2],[-1,-2]]def caculate_dis(point_1, point_2):     ## 計算當前點到終點的距離return ((point_1[0] - point_2[0]) ** 2 + (point_1[1] - point_2[1]) ** 2) ** 0.5    ### **2 表示平方， ** 0.5 表示sqrt()，即開根def A_star(start, end):dis = -1length = 1001q = [ (caculate_dis(start, end), start) ]   ## 隊列內存儲一個元組，元組包含了距離信息和起點位置。在小頂堆中會優先對元組中靠左的元素進行排序heapq.heappush(q, (caculate_dis(start, end), start))step = {start: 0}       ## 一個字典，來記錄從起點到當前節點所走過的距離。數組不能作為key值while q:        ## q是一個隊列，跟BFS的思路一樣dis, cur = heapq.heappop(q)     ## 推出小頂堆的堆頂if cur == end:      ## 當前節點抵達終點return step[cur]for x_move, y_move in directions:new_x = cur[0] + x_movenew_y = cur[1] + y_moveif new_x < 1 or new_x > 1000 or new_y < 1 or new_y > 1000:continuenew = (new_x, new_y)step_new = step[cur] + 1  #計算起點到當前節點所走過的距離，每走一次加一次if step_new < step.get(new, float('inf')):  ## 不存在new這個key時，輸出inf。 如果從起點出發有走更少的距離抵達目前這個點，則不更新step[new] = step_new  # 記錄從起點到當前節點所走過的距離heapq.heappush(q, (caculate_dis(new, end)+step[new], new))if __name__ == "__main__":test_num = int(input())for _ in range(test_num):start_x, start_y, end_x, end_y = map(int, input().split())start = (start_x, start_y)end = (end_x, end_y)min_List = A_star(start, end)print(min_List)

from collections import defaultdict
import math
import heapqdirections = [ [2,1], [2,-1],[1,2], [1, -2],[-2,1], [-2,-1],[-1,2], [-1,-2],]def caculate_dis(cur, end):         ## 這里不能改精度，會影響搜索dis = math.sqrt((cur[0] - end[0])**2 + (cur[1] - end[1])**2)return disdef A_star(start, end):queue = [(caculate_dis(start,end), start)]heapq.heappush(queue, (caculate_dis(start,end), start))step = {}step[start] = 0while queue:dis, cur = heapq.heappop(queue)if cur == end:return disfor x_move, y_move in directions:new_x = cur[0] + x_movenew_y = cur[1] + y_moveif new_x < 1 or new_x > 1000 or new_y < 1 or new_y > 1000:continuenew = (new_x, new_y)step_new = step[cur] + 1if step_new < step.get(new, float('inf')):step[new] = step_newheapq.heappush(queue, ((caculate_dis(new, end)+step_new),new))## 浮點數+整數 = 浮點數，后續堆result結果進行int轉換就行if __name__ == "__main__":test_num = int(input())for _ in range(test_num):start_x, start_y, end_x, end_y = map(int, input().split())start = (start_x, start_y)end = (end_x, end_y)min_result = A_star(start, end)print(int(min_result))

注意：

• 為什么需要這個判斷 if step_new < step.get(new, float('inf'))

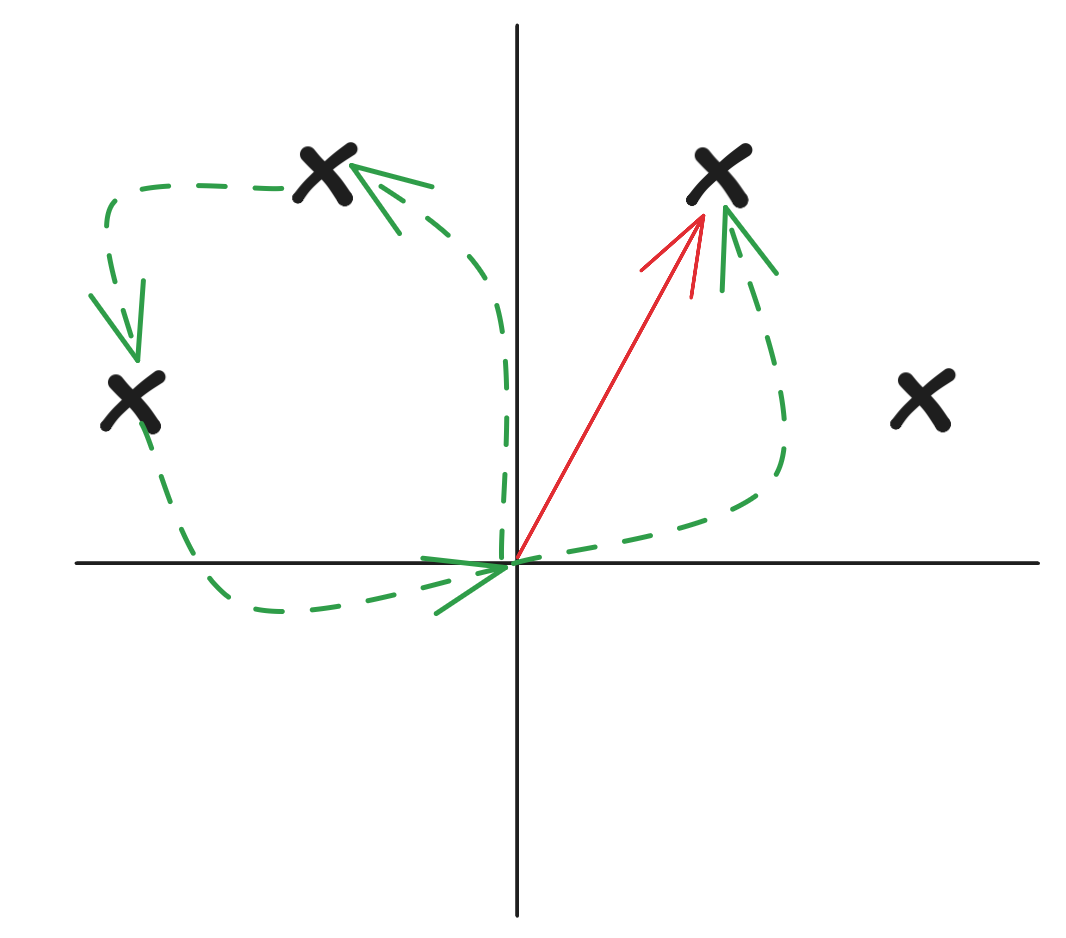
因為走到同一個節點下所用的步數可以步數，但我么要求的是所用步數最少的。如上，只有紅色箭頭是所花步數是最少的。

• 另外由于A*算法具有一定的方向性（小頂堆+dis實現），因此每次BFS只會選取一個更靠近終點的點進行下一次BFS，故不會存在因為重復遍歷而出現死循環的問題。

缺點：

• 小頂堆內維護了很多元組，但實際用到的時候只是使用到了堆頂。如果在一次路徑搜索中，大量不需要訪問的節點都在隊列里，會造成空間的過度消耗。
• A*算法只擅長給出明確的目標 然后找到最短路徑。如果給出 多個可能的目標，然后在這多個目標中 選擇最近的目標，則A * 就不擅長了。