目錄

一、集合框架

1、什么是集合框架

2、集合框架的重要性

2.1開發中的使用

2.2筆試及面試題

3、背后涉及的數據結構以及算法

3.1什么是數據結構

3.2容器背后對應的數據結構

3.3相關java知識

3.4什么是算法

3.5如何學好數據結構以及算法

二、時間和空間復雜度

1、算法的效率

2、時間復雜度

2.1時間復雜度的概念

2.2大O的漸進表示法

2.3推導大O階方法

2.4常見的時間復雜度計算舉例

三、空間復雜度

---

一、集合框架

1、什么是集合框架

????????Java集合框架(Java Collection Framework),又被稱為容器(container),是定義在java.util包下的一組接口(interfaces)和其實現類(classes).

????????主要表現為把多個元素(element)放在一個單元中,用于對這些元素進行快速、便捷的存儲（store）、檢索（retrieve）、管理（manipulate），即平時俗稱的增刪改查（CRUD）

類和接口總覽：

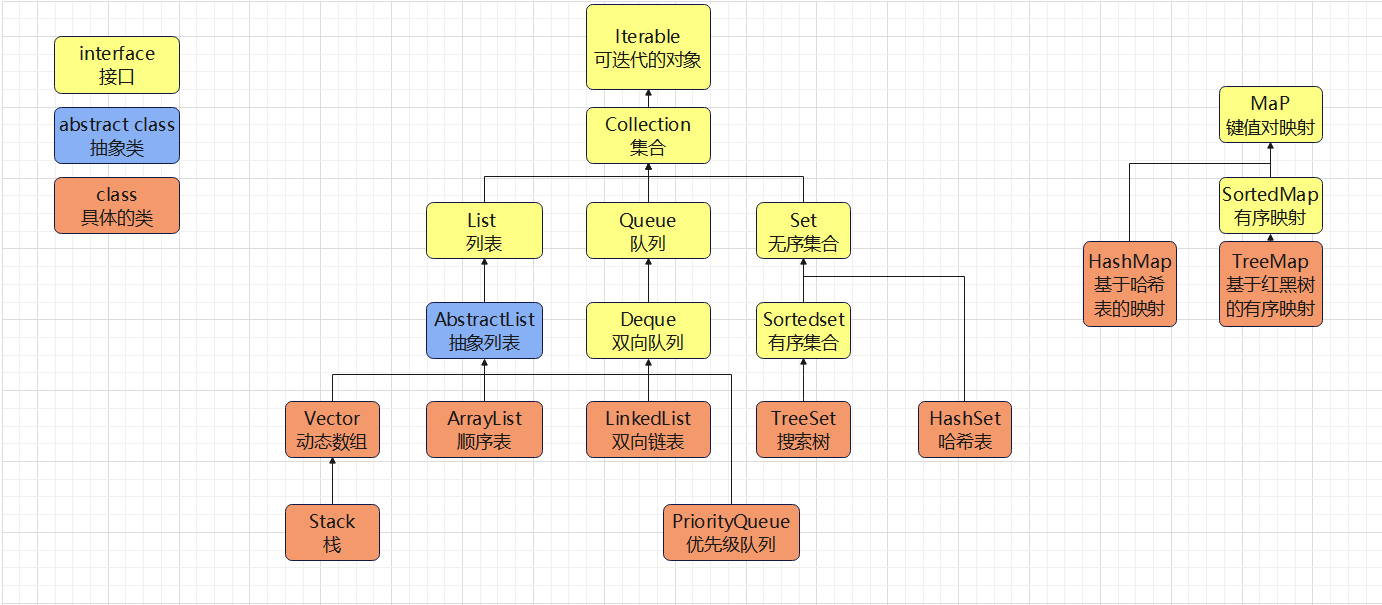
2、集合框架的重要性

2.1開發中的使用

（1）使用成熟的集合框架，有助于我們便捷、快速的寫出高效、穩定的代碼

（2）學習背后的數據結構知識，有助于我們理解各個集合的優缺點及使用場景

2.2筆試及面試題

? ? ? ? 在各廠的秋招中，常會用數據結構作為筆試的考題；不僅如此，哪怕是在面試中，也常常會問到我們一些數據結構相關的問題！！！

3、背后涉及的數據結構以及算法

3.1什么是數據結構

????????數據結構（Data Structure）是計算機存儲、組織數據的方式，指互相之間存在一種或多種特定關系的數據元素的集合

3.2容器背后對應的數據結構

????????在這里，我們主要學習以下容器，每個容器其實都是對某種特定數據結構的封裝，大概了解一下，后序會給大家詳細講解并模擬實現：

（1）Collection：一個接口，包含了大部分容器常用的一些方法

（2）List：一個接口，規范了ArrayList和LinkedList中要實現的方法

? ? ? ? ? ? ? ? ? ? ? ? ArrayList：實現了List接口，底層為動態類型順序表

? ? ? ? ? ? ? ? ? ? ? ? LinkedList：實現了List接口，底層為雙向鏈表

（3）Stack：底層是棧，棧是一種特殊的順序表

（4）Queue：底層是隊列，隊列是一種特殊的順序表

（5）Deque：是一個接口

（6）Set：集合，是一個接口，里面放置的是K模型

? ? ? ? ? ? ? ? ? ? ? ? HashSet：底層為哈希桶，查詢的時間復雜度為O(1)

? ? ? ? ? ? ? ? ? ? ? ? TreeSet：底層為紅黑樹，查詢的時間復雜度為O( logN ),關于key有序的

（7）Map：映射，里面存儲的是K-V模型的鍵值對

? ? ? ? ? ? ? ? ? ? ? ? ?HashMap：底層為哈希桶，查詢時間復雜度為O(1)

? ? ? ? ? ? ? ? ? ? ? ? ?TreeMap：底層為紅黑樹，查詢的時間復雜度為O(logN)，關于key有序

3.3相關java知識

（1）泛型?（Generic）

（2）自動裝箱 （autobox） 和自動拆箱 （autounbox）

（3）Object 的 equals 方法

（4）Comparable 和 Comparator 接口

3.4什么是算法

????????算法(Algorithm):就是定義良好的計算過程，他取一個或一組的值為輸入，并產生出一個或一組值作為輸出。簡單來說算法就是一系列的計算步驟，用來將輸入數據轉化成輸出結果。

3.5如何學好數據結構以及算法

? ? ? ? 不少人都會問：怎么才能學會學好數據結構呢？？？

(1)死磕代碼，磕成這樣就可以了

（2）注意畫圖和思考

? ? ? ? 在我看來，學數據結構主要分為這樣的過程：

思考==>畫圖==>寫代碼（N）==>畫圖==>再次寫代碼==>調試==>……

#注：一定要畫圖！！！一定要畫圖！！！一定要畫圖！！！

（3）多看兩遍我的博客或者自己寫點的東西（如博客），多做總結

（4）多刷題

? ? ? ? 可以在牛客網和LeetCode上面刷一下相關的數據結構，看一下不同的解題思路！！！

二、時間和空間復雜度

? ? ? ? 首先要明確，我們不只是說只要可以實現、完成任務就可以，而是要盡可能用更少的時間、更少的空間來完成任務！！！（就像是干活一樣，不僅要老板滿意，還要在保證質量的情況下用最短的時間以及最少的成本完成工作，讓利益最大化！！！）

1、算法的效率

????????算法效率分析分為兩種：第一種是時間效率，第二種是空間效率。時間效率被稱為時間復雜度，而空間效率被稱作空間復雜度。時間復雜度主要衡量的是一個算法的運行速度，而空間復雜度主要衡量一個算法所需要的額外空間

（在計算機發展的早期，計算機的存儲容量很小。所以對空間復雜度很是在乎。但是經過計算機行業的迅速發展，計 算機的存儲容量已經達到了很高的程度。所以我們如今已經不需要再特別關注一個算法的空間復雜度。但是，一些面試題或者筆試題中有要求！！！）

2、時間復雜度

2.1時間復雜度的概念

????????時間復雜度的定義：在計算機科學中，算法的時間復雜度是一個數學函數，它定量描述了該算法的運行時間。一個算法執行所耗費的時間，從理論上說，是不能算出來的，只有你把你的程序放在機器上跑起來，才能知道。但是我們需要每個算法都上機測試嗎？是可以都上機測試，但是這很麻煩，所以才有了時間復雜度這個分析方式。一個算法所花費的時間與其中語句的執行次數成正比例，算法中的基本操作的執行次數，為算法的時間復雜度。

2.2大O的漸進表示法

 // 請計算一下func1基本操作執行了多少次？void func1(int N){int count = 0;for (int i = 0; i < N ; i++) {for (int j = 0; j < N ; j++) {count++;}}//N^2for (int k = 0; k < 2 * N ; k++) {count++;}//2*Nint M = 10;while ((M--) > 0) {count++;}//10System.out.println(count);}

Func1 執行的基本操作次數 ：

????????????????????????????????????????????????????????F（N） = N^2 + 2*N + 10

（1）N = 10? ? ? ?F(N) = 130

（2）N = 100? ? ?F(N) = 10210

（3）N = 1000? ?F(N) = 1002010

????????實際我們計算時間復雜度時，我們只需要算大概執行的次數，也就是大O的漸進表示法

????????大O符號（Big O notation）：是用于描述函數漸進行為的數學符號。

2.3推導大O階方法

（1）用常數1取代運行時間中的所有加法常數（換常數）

（2）在修改后的運行次數函數中，只保留最高階項（只保留最高相）

（3）如果最高階項存在且不是1，則去除與這個項目相乘的常數。得到的結果就是大O階。（系數變成1）

????????使用大O的漸進表示法以后，Func1的時間復雜度為：O（N^2）

（1）N = 10? ? ? ?F(N) = 100

（2）N = 100? ? ?F(N) = 10000

（3）N = 1000? ?F(N) = 1000000

????????通過上面我們會發現大O的漸進表示法去掉了那些對結果影響不大的項，簡潔明了的表示出了執行次數。 另外有些算法的時間復雜度存在最好、平均和最壞情況：

????????最壞情況：任意輸入規模的最大運行次數(上界)（最慢）

????????平均情況：任意輸入規模的期望運行次數

????????最好情況：任意輸入規模的最小運行次數(下界)（最快）

如：在一個長度為N數組中搜索一個數據x

????????最好情況：1次找到

????????最壞情況：N次找到

????????平均情況：N/2次找到

?在實際中一般情況關注的是算法的最壞運行情況，所以數組中搜索數據時間復雜度為O(N)

2.4常見的時間復雜度計算舉例

實例1：

void func3(int N, int M) {int count = 0; for (int k = 0; k < M; k++) {count++;//M} for (int k = 0; k < N ; k++) {count++;//N} System.out.println(count);}

????????由于基本操作執行了N+M次，并且兩數都是未知數，所以時間復雜度為O（N+M）

實例二：

void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}//N*(N-1)/2} if (sorted == true) {break;}}}

????????由于循環執行，第一次執行（N-1）次，最后一次執行了0次，共N次，求每次比前一次少一次，因此得到N*(N-1)/2，因此時間復雜度為O(N^2)

實例三：

int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;}

????????二分查找，一次是原來的一半可以得出（N/2）^O=1,計算可得時間復雜度為O（logN）(logN是以2為底，lgN是以10為底)

實例四：

 long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;}

????????階乘遞歸是在比較N和2的大小關系進行選擇，可以發現共遞歸了N次，所以時間復雜度為O(N)

實例五：

 int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);}

? ? ? ? 我們可以發現，左側最頂端（第一次）是（N-1）,最后一次是1，也就可以得到近似的1+2^1+……+2^（N-1）,也就是2^N-1,同理，右側也可以計算出是2^(N-1)-1，因此時間復雜度為O(2^N)

????????我們常遇到的復雜度有：O(1) < O(logN) < O(N) < O(N*logN) < O(N^2)

三、空間復雜度

????????空間復雜度是對一個算法在運行過程中臨時占用存儲空間大小的量度 。空間復雜度不是程序占用了多少bytes的空間，因為這個也沒太大意義，所以空間復雜度算的是變量的個數。空間復雜度計算規則基本跟時間復雜度類似，也使用大O漸進表示法。

實例一：

void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}
}

????????因為使用了常數個額外空間，所以空間復雜度為O(1)

實例二：

 int[] fibonacci(int n) {long[] fibArray = new long[n + 1];fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;}

????????因為動態開辟了N個空間，空間復雜度為 O(N）

實例三：

 long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;}

因為遞歸調用了N次，開辟了N個棧幀，每個棧幀使用了常數個空間，因此空間復雜度為O(N）

?????????????????由于內容較多，會分為多篇講解，預知后續內容，請看后續博客！！！