深度學習(Deep Learning, DL)是機器學習(Machine Learning, ML)的一個重要分支,核心是通過模擬人類大腦神經元的連接方式,構建多層神經網絡來自動學習數據中的特征和規律,最終實現預測、分類、生成等任務。它擺脫了傳統機器學習對 “人工設計特征” 的依賴,能直接從原始數據(如圖像、文本、音頻)中挖掘深層信息,是當前人工智能(AI)技術爆發的核心驅動力。
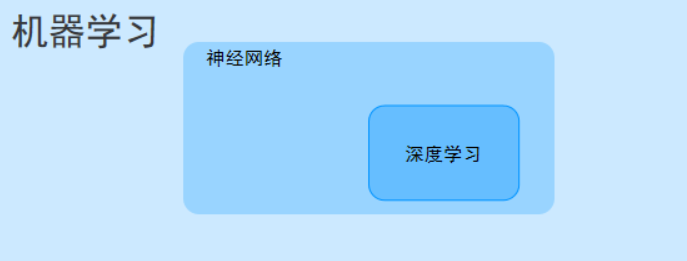
一、深度學習的核心思想:“多層” 與 “自動特征學習”
要理解深度學習,首先需要對比它與傳統機器學習的核心差異:

舉個直觀例子:
- 用傳統機器學習識別貓:需手動設計 “是否有胡須”“是否有尖耳朵”“毛色分布” 等特征,再喂給模型訓練;
- 用深度學習識別貓:直接輸入原始貓的圖片,模型會自動從 “像素點→邊緣→紋理→五官→完整貓輪廓” 逐層學習特征,無需人工干預。
二、深度學習的基礎組件:神經網絡的核心單元
深度學習的模型本質是多層神經網絡,其最小組成單元和結構如下:
1. 基本單元:人工神經元(Artificial Neuron)
模擬生物神經元的 “接收信號→處理信號→輸出信號” 過程,是神經網絡的基礎:
? 輸入(Input):接收來自前一層的信號(如數據特征、前一層神經元的輸出);
? 權重(Weight):每個輸入對應一個權重(表示該輸入的重要性,模型訓練的核心就是優化權重);
? 偏置(Bias):調整神經元激活的 “基準線”,避免僅由輸入和權重決定輸出;
? 激活函數(Activation Function):對 “輸入 × 權重 + 偏置” 的結果進行非線性變換,讓模型能學習復雜的非線性關系(如圖像、語言中的復雜規律)。
常見激活函數:
- ReLU:最常用,公式?
f(x) = max(0, x),解決 “梯度消失” 問題,計算高效; - Sigmoid:將輸出壓縮到 [0,1],適用于二分類任務的輸出層;
- Tanh:將輸出壓縮到 [-1,1],比 Sigmoid 更對稱,常用于早期模型的隱藏層。
- 這是生物上的神經元
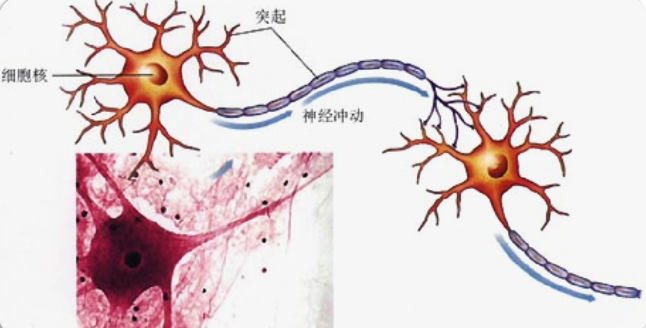
- 這是計算機上的神經網絡、
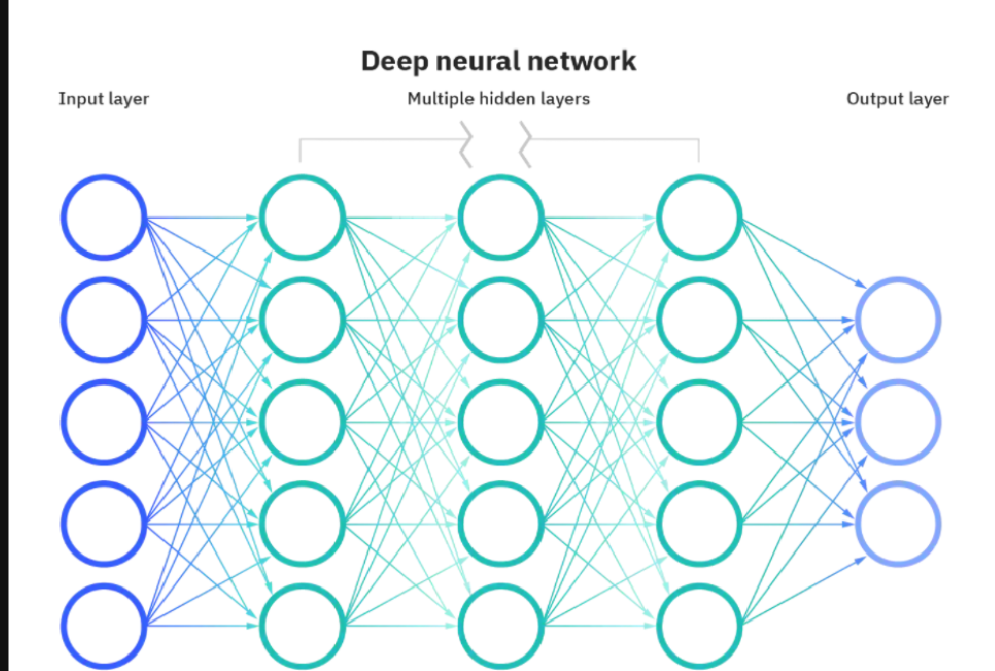
- 神經網絡是由大量的節點(或稱“神經元”)和之間相互的聯接構成。
- 每個節點代表一種特定的輸出函數,稱為激勵函數、激活函數(activation function)。
- 每兩個節點間的聯接都代表一個對于通過該連接信號的加權值,稱之為權重,這相當于人工神經網絡的記憶。
2. 神經網絡的層結構
多個人工神經元按 “層” 組織,形成神經網絡,核心層包括:
? 輸入層(Input Layer):接收原始數據(如圖片的像素值、文本的向量),僅傳遞數據,不做計算;
? 隱藏層(Hidden Layer):對輸入層的信號進行逐層加工、提取特征,“深度” 即指隱藏層的數量(通常≥2 層即可稱為 “深度網絡”);
? 輸出層(Output Layer):輸出模型的最終結果,根據任務類型選擇不同的激活函數:
? 分類任務:用 Softmax(多分類,輸出各類別概率之和為 1);
? 回歸任務:無激活函數(直接輸出連續值);
? 二分類任務:用 Sigmoid(輸出單個概率值)。
三、推導
- 以下是推導過程:
- 傳入特征,按照不同的權重傳入神經元進行求和
- 然后將結果放入sigmod函數進行非線性映射
- 最后得出分類結果

四、感知器與多層感知器
1.感知器
- 由兩層神經元組成的神經網絡--“感知器”(Perceptron),感知器只能線性劃分數據。
- 因為只能通過一個線性函數(即加權和)將輸入數據映射到輸出類別
- 感知器圖示
- 右下角是計算規則
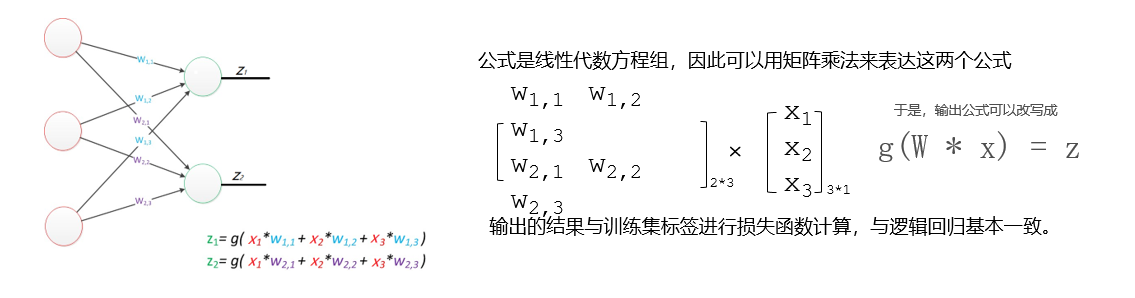
2.多層感知器
多層感知器(MLP)是深度學習中一種重要的神經網絡結構,由多個層次的神經元組成,通常包括以下部分:
輸入層:接收數據特征。
隱藏層:一個或多個,進行復雜的非線性變換。每層的神經元通過激活函數(如ReLU、Sigmoid)處理輸入。
輸出層:生成最終的預測結果或分類標簽。
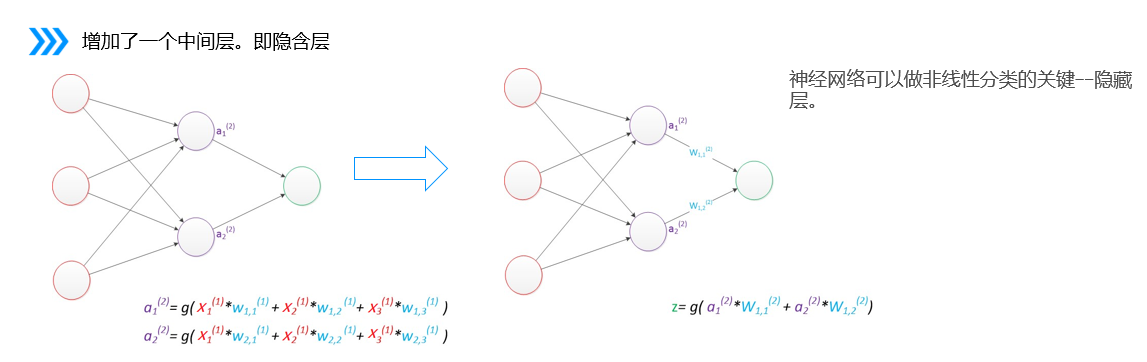
3.偏置
在神經網絡中需要默認增加偏置神經元(節點),這些節點是默認存在的
它本質上是一個只含有存儲功能,且存儲值永遠為1的單元
在神經網絡的每個層次中,除了輸出層以外,都會含有這樣一個偏置單元
偏置節點沒有輸入(前一層中沒有箭頭指向它)
一般情況下,我們都不會明確畫出偏置節點
調整決策邊界:偏置項允許決策邊界在特征空間中進行平移,而不僅僅是通過原點。
提高模型靈活性:使得神經網絡能夠捕捉到更多的數據模式和復雜性,即使在沒有輸入特征的情況下也能進行調整。
五、如何確定輸入層和輸出層個數
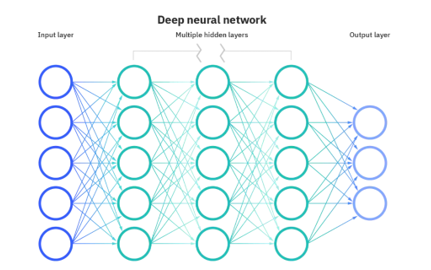
- 輸入層的節點數:與特征的維度匹配
- 輸出層的節點數:與目標的維度匹配。
- 中間層的節點數:目前業界沒有完善的理論來指導這個決策。一般是根據經驗來設置。較好的方法就是預先設定幾個可選值,通過切換這幾個值來看整個模型的預測效果,選擇效果最好的值作為最終選擇。
六、損失函數
模型訓練的目的:使得參數盡可能的與真實的模型逼近。
具體做法:
1、首先給所有參數賦上隨機值。我們使用這些隨機生成的參數值,來預測訓練數據中的樣本。????
2、計算預測值為yi,真實值為y。那么,定義一個損失值loss,損失值用于判斷預測的結果和真實值的誤差,誤差越小越好
常用的損失函數: 0-1損失函數 均方差損失 平均絕對差損失 交叉熵損失 合頁損失
多分類的情況下,如何計算損失值
![]()
七、正則化懲罰
輸入為[1,0,0,0]現有2種不同的權重值
w1 = [1,0,0,0]
w2 = [0.25,0.25,0.25,0.25]
w1和w2與輸入的乘積都為1,但w2 與每一個輸入數據進行計算后都有數據,使得w2會學習到每一個特征信息。而w1只和第1個輸入信息有關系,容易出現過擬合現象,因此w2的效果會比w1 好
正則化懲罰的功能:主要用于懲罰權重參數w,一般有L1和L2正則化。
八、梯度下降
1. 偏導數
????????我們知道一個多變量函數的偏導數,就是它關于其中一個變量的導數而保持其他變量恒定。該函數的整個求導: 例如:計算像 f(b0,b1)=b0x12* b1x2 這樣的多變量函數的過程可以分解如下:

2. 梯度
梯度可以定義為一個函數的全部偏導數構成的向量,梯度向量的方向即為函數值增長最快的方向
3、梯度下降法
一個一階最優化算法,通常也稱為最陡下降法 ,要使用梯度下降法找到一個函數的局部極小值
步長(學習率):梯度可以確定移動的方向。學習率將決定我們采取步長的大小。不易過小和過大 如何解決全局最小的問題?產生多個隨機數在不同的位置分別求最小值。
九、BP神經網絡
BP(Back-propagation,反向傳播)前向傳播得到誤差,反向傳播調整誤差,再前向傳播,再反向傳播一輪一輪得到最優解的。
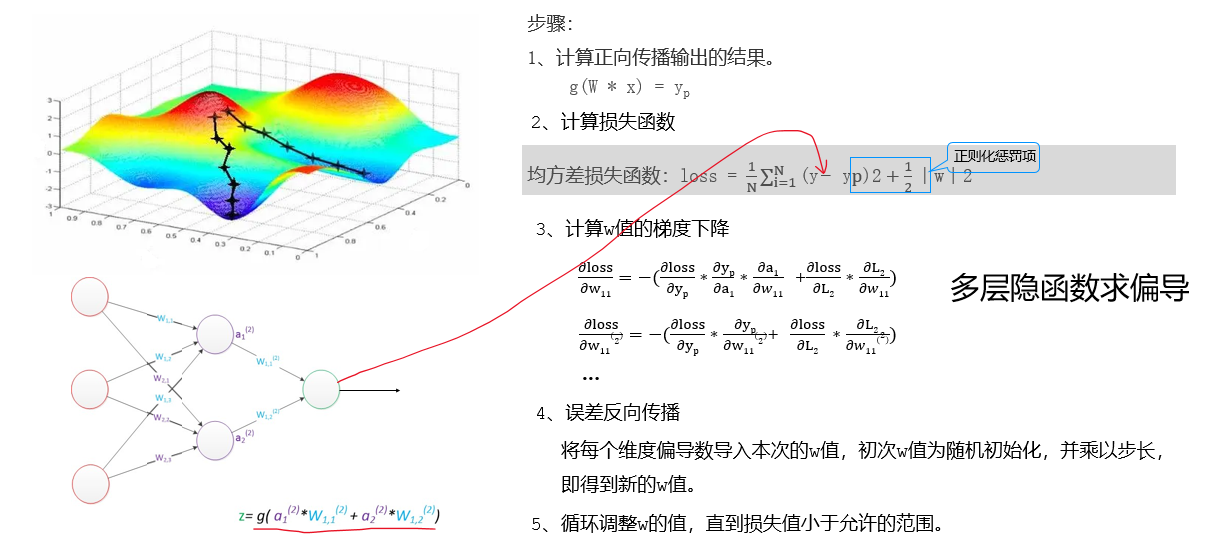



)









![Flutter上手記:為什么我的按鈕能同時在iOS和Android上跳舞?[特殊字符][特殊字符]](http://pic.xiahunao.cn/Flutter上手記:為什么我的按鈕能同時在iOS和Android上跳舞?[特殊字符][特殊字符])


/電影評論/網站系統/電影/評論/網站/系統/影評網站/電影網站/評論系統/電影評論系統)


