本文筆者將帶領讀者一起學習鏈式二叉樹的一些基本語法，至于更難一些的插入刪除等，筆者將在后續C++更新后再次詳細帶領大家學習。

首先，在進行二叉樹之前，我們需要一顆二叉樹，而二叉樹的初始化現階段實現不太現實，故筆者在此處手動建一個二叉樹：由于現在不是堆了，所以用數組顯然是不行，這時候我們直接用鏈表存儲即可，也就是鏈式二叉樹：

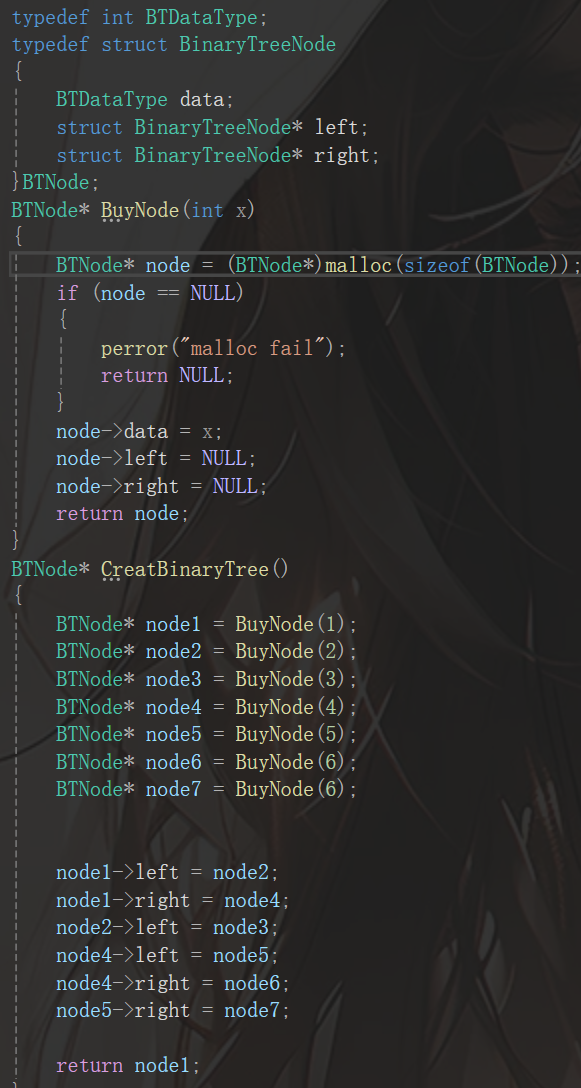
如上圖，首先初始化了一個節點，然后兩個指針分別指向左子樹和右子樹，然后手動賦值即可，最終的二叉樹長這樣：

? ? ? ? 1
? ? ? ?/ \
? ? ? 2 ? 4
? ? ?/ ? / \
? ? 3 ? 5 ? 6
? ? ? ? ?\
? ? ? ? ? 7

下面我們只對這個二叉樹進行討論，首先進行遍歷，二叉樹的遍歷有三次，分別是：前序遍歷，中序遍歷，后序遍歷。

前序遍歷：根節點，左子樹，右子樹。由于三種遍歷方式本質一樣，筆者在此著重講一下第一種遍歷方式。首先，根據這棵樹，我們可以借用遞歸的思想，不過這里有一個易錯點，那就是左（右）子樹是空節點時仍然存在這種情況，這里筆者記作N，一定不能忽略這種情況，比如筆者創建的這棵樹，如果按照前序遍歷，那就是1 （2 （3?N N） N）（ 4 （5 N （7 N N））（ 6 N N））不難理解，這其實是一種遞歸的思想，不斷推進，直到遇到了N（空結點），剩下情況一直保證先根在左最后右，這是邏輯角度，下面從代碼的角度來分析：

這就是一個前序遍歷的代碼實現，其實不難理解，這就是用了遞歸思想，函數棧幀的知識，因為本質上就是棧幀的調用，在具體進行時，首先需要讓左子樹處理完，在這之后才能進行右子樹，每個二叉樹都是如此進行，具體可以看下圖：

左圖有些問題，不過無傷大雅，思路就是如此，最后再main函數調用一下即可：

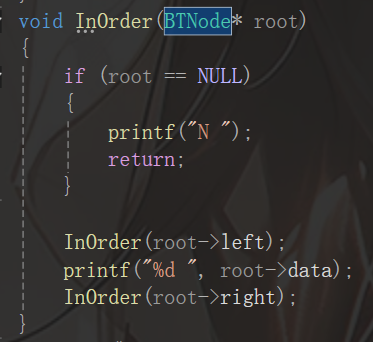
中序遍歷：左子樹，根節點，右子樹

? ? ? ? 1
? ? ? ?/? \
? ? ? 2 ? 4
? ? ?/? ? /? ? \
? ? 3 ? 5 ? 6
? ? ? ? ? \
? ? ? ? ? ?7

中序遍歷和前序遍歷的情況基本一致，并無不同，中序遍歷結果：（（N 3 N）?2??N ）1 （（N? 5 （N 7 N ）））4? （N 6 N））

代碼自然也是類似的：

這里不作過多解釋，相信讀者都能理解。

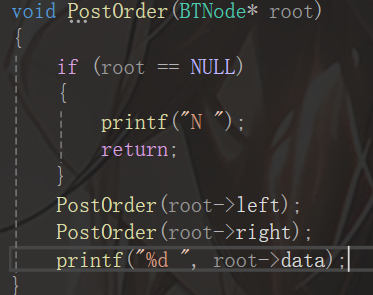
后序遍歷：左子樹，右子樹，根節點

N N 3 N 2 N N 7 N 5 N N 6 4 1
下面直接看代碼：

到這里，三種遍歷方式其實已經結束，最后，筆者給大家看一下打印的結果：?

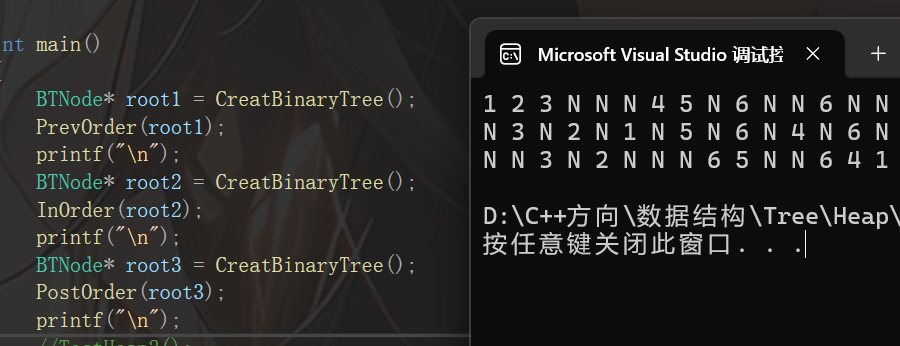
ok,到這里筆者就結束了，筆者把源碼放在GitHub上了，希望大家給一個星星：

https://github.com/z-yi-han/Fundamentals-of-Data-Struct/tree/main/Tree

筆者還會持續更新，希望大家支持，非常感謝各位讀者

?