1. 題意

給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之后能接多少雨水。

2. 題解

這個題不會做，全部是看得題解捏。

不過能看懂題解感覺自己也很棒了！

看完題解后感覺最難的是如何求出有多少積水，

答案直接給的是當前位置的積水量是它左右兩邊兩個最大值的最小值

減去當前的高度。

靈茶山艾府的題解中解釋了為什么？如果比兩端最高的高積水肯定會

從一側流出去。

不過我肯定是想不到的。

有了這個結論之后，其實就可以做一下了。

對于每個高度，求出它左右兩側的最高高度，從而計算積水的高度。

2.1 前后綴最大值

算出前后綴的最高高度。

再遍歷一次計算積水量。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int ans = 0;vector<int> left_max(n, 0);vector<int> right_max(n, 0);for (int i = 1; i < n; ++i) {left_max[i] = max(left_max[i - 1], height[i - 1]);}for (int i = n - 2; ~i; --i) {right_max[i] = max(right_max[i + 1], height[i + 1]);}for (int i = 1; i < n - 1; ++i) {ans += max(0, min(left_max[i], right_max[i]) - height[i] );}return ans;}
};

當然可以稍微優化下空間，不過差別不大。

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int ans = 0;vector<int> rightMx(n + 1, -1);for (int i = n - 1; ~i; --i) {rightMx[i] = max(height[i], rightMx[i + 1]);}int leftMx = height[0];for (int i = 1; i < n - 1; ++i) {ans += max( 0, min(leftMx, rightMx[i + 1]) - height[i]);leftMx = max(height[i], leftMx);}return ans;}
};

時間復雜度$O(n)$

空間復雜度$O(n)$

2.2 雙指針

雙指針的解法確實比較巧妙，先說下做法，再證明為什么正確，最后給出代碼。

思路是，左指針$l$指向左端，右指針$r$指向右端，同時維護兩個變量：

$leftMax$表示$l$左端的最大值，

$rightMax$表示$r$右端的最大值。

當$leftMax<rightMax$時，

左指針元素積水高度為$leftMax?height[l]$，左指針右移。

當$leftMax\ge rightMax$時，

右指針元素積水高度為$rightMax?height[r]$，右指針左移。

為什么這個策略正確呢? 下面簡要證明。

我們令lmx(i)=max?{height[k],0≤k≤i}lmx(i) = \max\{height[k] , 0 \le k \le i\}lmx(i)=max{height[k],0≤k≤i}，

也就是$lmx(i)$表示下標$i$左端的最大值。

我們令rmx(i)=max?{height[k],i≤k≤n?1}rmx(i)=\max\{ height[k],i \le k \le n-1\}rmx(i)=max{height[k],i≤k≤n?1},

也就是$rmx(i)$表示下標$i$右端的最大值。

我們令$w[i]$表示位置$i$的積水高度，

那么$w[i]=\min (lmx(i),rmx(i))?height[i]$。

當$l\le r$時，我們很容易得到

$$\begin{gathered} lmx(l)\le lmx(r) \\ rmx(l)\ge rmx(r) \end{gathered}$$

上面的$leftMax$相當于$lmx(l)$，$rightMax$相當于$rmx(r)$。

當$lmx(l)<rmx(r)$時，必然有$lmx(l)<rmx(r)\le rmx(l)$，

因此$\min (lmx(l),rmx(l))=lmx(l)$。

同理$lmx(l)\ge rmx(r)$時，必然有$rmx(r)\le lmx(l)\le lmx(r)$，

因此$\min (lmx(r),rmx(r))=rmx(r)$。

綜上，這個策略是正確的。

下面給出不那么重要的代碼：

class Solution {
public:int trap(vector<int>& height) {int n = height.size();int ans = 0;int l = 0;int r = n - 1;int leftMax = 0;int rightMax = 0;while (l <= r) {leftMax = max( leftMax, height[l]);rightMax = max( rightMax, height[r]);if ( height[l] < height[r]) {ans += leftMax - height[l];++l;}else {ans += rightMax - height[r];--r;}}return ans;}
};

時間復雜度$O(n)$

空間復雜度$O(1)$

2.3 單調棧

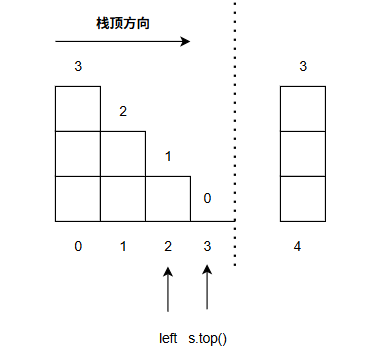
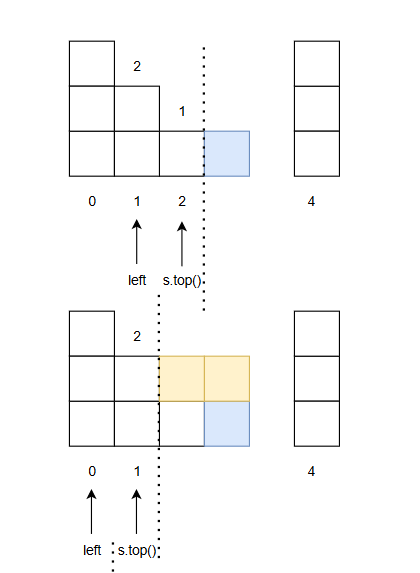
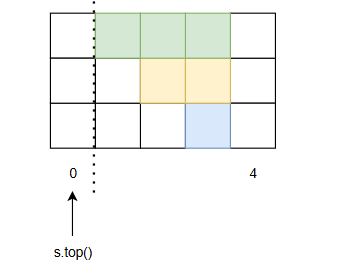
說實話不是很明白單調棧的做法怎么想到的，

它比前后綴的做法要難理解的多，也不知道怎么來的，純純為了

用一下這個數據結構？

核心思想是逐步填充積水高度。

當棧頂元素大于新元素時，直接將新元素入棧。

否則，將棧頂元素出棧，令為$k$，

將積水高度填充到與新棧頂$left$或新元素$height[i]$的最小值，

即$\min (height[i],height[left])?height[k]$

填充的寬度就是$i?left?1$

不斷重復這個過程直到棧空或者棧頂大于新元素，再將新元素入棧。

敘述起來很復雜，還是看下圖吧，像個一步步填坑的過程。

下面給出代碼

class Solution {
public:int trap(vector<int>& height) {int n = height.size();stack<int> s;int ans = 0;for (int i = 0; i < n; ++i) { while (!s.empty() && height[s.top()] <= height[i]) {int k = s.top();s.pop();if (!s.empty()) {int left = s.top();ans += ( i - left - 1 ) * (min(height[i], height[left]) - height[k] );}}s.push( i );}return ans;}
};

時間復雜度$O(n)$，空間復雜度$O(n)$

3. 參考

leetcode
0x3f