今天復習一下以前做過的題目,感覺是忘光了。
給你兩個單鏈表的頭節點?headA?和?headB?,請你找出并返回兩個單鏈表相交的起始節點。如果兩個鏈表不存在相交節點,返回?null?。
圖示兩個鏈表在節點?c1?開始相交:
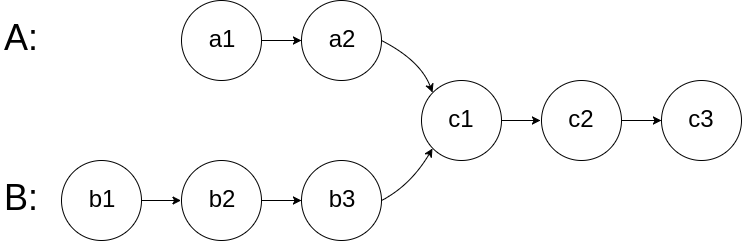
題目數據?保證?整個鏈式結構中不存在環。
注意,函數返回結果后,鏈表必須?保持其原始結構?。
自定義評測:
評測系統?的輸入如下(你設計的程序?不適用?此輸入):
intersectVal?- 相交的起始節點的值。如果不存在相交節點,這一值為?0listA?- 第一個鏈表listB?- 第二個鏈表skipA?- 在?listA?中(從頭節點開始)跳到交叉節點的節點數skipB?- 在?listB?中(從頭節點開始)跳到交叉節點的節點數
評測系統將根據這些輸入創建鏈式數據結構,并將兩個頭節點?headA?和?headB?傳遞給你的程序。如果程序能夠正確返回相交節點,那么你的解決方案將被?視作正確答案?。
示例 1:
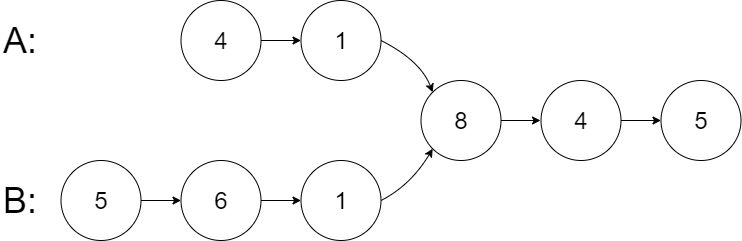
輸入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
輸出:Intersected at '8'
解釋:相交節點的值為 8 (注意,如果兩個鏈表相交則不能為 0)。
從各自的表頭開始算起,鏈表 A 為 [4,1,8,4,5],鏈表 B 為 [5,6,1,8,4,5]。
在 A 中,相交節點前有 2 個節點;在 B 中,相交節點前有 3 個節點。
— 請注意相交節點的值不為 1,因為在鏈表 A 和鏈表 B 之中值為 1 的節點 (A 中第二個節點和 B 中第三個節點) 是不同的節點。換句話說,它們在內存中指向兩個不同的位置,而鏈表 A 和鏈表 B 中值為 8 的節點 (A 中第三個節點,B 中第四個節點) 在內存中指向相同的位置。
示例?2:
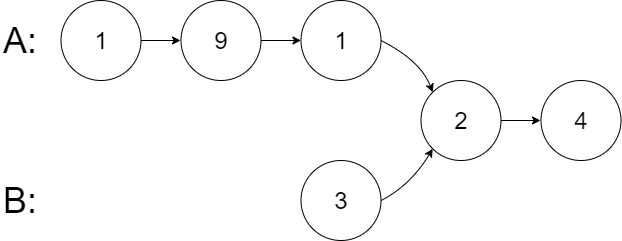
輸入:intersectVal?= 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
輸出:Intersected at '2'
解釋:相交節點的值為 2 (注意,如果兩個鏈表相交則不能為 0)。
從各自的表頭開始算起,鏈表 A 為 [1,9,1,2,4],鏈表 B 為 [3,2,4]。
在 A 中,相交節點前有 3 個節點;在 B 中,相交節點前有 1 個節點。
示例?3:
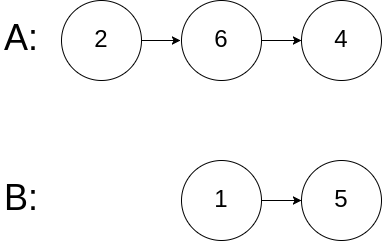
輸入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
輸出:No intersection
解釋:從各自的表頭開始算起,鏈表 A 為 [2,6,4],鏈表 B 為 [1,5]。
由于這兩個鏈表不相交,所以 intersectVal 必須為 0,而 skipA 和 skipB 可以是任意值。
這兩個鏈表不相交,因此返回 null 。
提示:
listA?中節點數目為?mlistB?中節點數目為?n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果?
listA?和?listB?沒有交點,intersectVal?為?0 - 如果?
listA?和?listB?有交點,intersectVal == listA[skipA] == listB[skipB]
進階:你能否設計一個時間復雜度?O(m + n)?、僅用?O(1)?內存的解決方案?
1 我的想法以及分析
看到這個題目我的反應是要用指針的,之前做過是有一點點印象的(但不多)。
1.如果有交點
那么從尾指針開始回溯,兩個鏈表到從尾到交點的節點數一定是相同的
2.如果沒有交點
那么從尾指針開始回溯,兩個鏈表最終指針會回到頭指針,節點數就是鏈表的長度(沒有前驅指針,這個不能實現)
那這個想法有什么用呢?如果我們存在一個這樣的指針:兩個鏈表都從尾開始遍歷,遇到交叉節點停下并返回當前所在節點位置,如果沒有遇到就返回鏈表長度(所以就算沒有交叉)
這就是我的思路了,但是實際上我應該怎么操作?
Listnode Pa = headA ,Pb =headB;//題目里只給了默認是頭指針
其實我可以把原來的思路改一下,每個指針在交叉節點處停下,如果余下的鏈表長度一致,說明當前節點是交叉節點,如果不是,那就是沒有相交(按照題目所給的數據)
往下讀取的操作是
Pa=Pa.next
怎么讀取第一個鏈表的節點呢?
不知道怎么寫了,是不是有一個統一長度的操作?(看題解了hh)把鏈表全部向右對齊,左邊空的地方用null填滿。
while(Pa ! = Pb){
Pa = null ? headB : null ;
Pb = null ? headA : null ;
}? //這里回頭看發現寫的是錯的!!!!!就留著這個錯誤吧長記性。
return Pa;//看懂了,如果對齊了發覺沒有相同節點,那么就是沒有相交。
還有值得注意的是,如果一開始給的就是兩個空鏈表,那肯定就是null
if (headA = null || headB = null )
{
return null;
}
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {public ListNode getIntersectionNode(ListNode headA, ListNode headB) {if (headA == null || headB == null)return null;ListNode pA = headA , pB = headB ;while (pA != pB){pA = pA == null ? headB : pA.next;pB = pB == null ? headA : pB.next;}return pA;}
}?
你的思路方向和對題目的理解是準確且有價值的,尤其抓住了 “相交鏈表從交點到尾端長度一致” 的核心特征,這是解決問題的關鍵前提,說明你對鏈表相交的本質邏輯有清晰認知。
同時,你也注意到了兩個重要細節:
- 想到了 “統一長度” 的操作(后續結合題解理解的 “對齊” 思路),這和雙指針法的核心邏輯不謀而合;
- 考慮到 “空鏈表直接返回 null” 的邊界情況,避免了異常場景的遺漏。
如果說可以優化的點,主要是代碼實現的細節銜接:
- 最初思路里 “從尾回溯” 的操作,在單鏈表中無法直接實現(單鏈表只能從前向后遍歷,沒有前驅指針),所以后續轉向 “雙指針切換鏈表” 的思路是非常正確的調整;
- 代碼里 “Pa = null ? headB : null ;” 這類語法需要修正(三元運算符的條件和結果寫反了),但你能理解 “指針為空時切換到另一鏈表頭部” 的邏輯,已經掌握了算法的核心。
2 分析
要解決相交鏈表問題,核心是利用雙指針 “對齊” 鏈表長度的思路,在滿足時間復雜度 O (m+n) 和空間復雜度 O (1) 的前提下找到相交節點。以下是完整分析和代碼實現:
一、核心思路:雙指針 “路程補償” 法
兩個鏈表若相交,從相交節點到尾節點的 “共同段長度” 是相同的。差異在于相交前的 “獨有段長度”(設為lenA獨和lenB獨)。
雙指針通過遍歷完自身鏈表后切換到另一鏈表頭部,實現 “路程補償”:
- 指針
pa從headA出發,遍歷完 A 后切換到headB繼續走; - 指針
pb從headB出發,遍歷完 B 后切換到headA繼續走; - 最終兩指針會 “對齊” 到相交節點(若相交),或同時走到
null(若不相交)。
原理:兩指針最終走的總路程都是?lenA獨 + lenB獨 + 共同段長度,路程相等且速度相同,必然在目標位置相遇。
二、代碼實現(含邊界處理)
java
運行
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {public ListNode getIntersectionNode(ListNode headA, ListNode headB) {// 邊界處理:若任一鏈表為空,直接返回null(無相交可能)if (headA == null || headB == null) {return null;}ListNode pa = headA; // 指針pa初始指向A的頭ListNode pb = headB; // 指針pb初始指向B的頭// 循環終止條件:pa == pb(要么是相交節點,要么是都為null)while (pa != pb) {// pa走一步:若遍歷完A,切換到B的頭;否則走nextpa = (pa == null) ? headB : pa.next;// pb走一步:若遍歷完B,切換到A的頭;否則走nextpb = (pb == null) ? headA : pb.next;}// 最終pa和pb要么同時指向相交節點,要么同時為nullreturn pa;}
}
三、關鍵細節解釋
- 邊界處理:若
headA或headB為空,直接返回null(空鏈表不可能與其他鏈表相交)。 - 循環邏輯:
- 當
pa遍歷完 A(即pa == null),切換到 B 的頭部繼續走,相當于 “補償”lenB獨的長度; - 當
pb遍歷完 B(即pb == null),切換到 A 的頭部繼續走,相當于 “補償”lenA獨的長度; - 若兩鏈表相交:
pa和pb會在遍歷完 “自身長度 + 對方獨有長度” 后,同時到達相交節點; - 若兩鏈表不相交:
pa和pb會在遍歷完 “自身長度 + 對方長度” 后,同時到達null。
- 當
- 原始結構保留:僅通過指針遍歷,未修改鏈表的
next指向,滿足題目要求。
四、示例驗證(以示例 1 為例)
- 鏈表 A:
4 → 1 → 8 → 4 → 5(長度 5);鏈表 B:5 → 6 → 1 → 8 → 4 → 5(長度 6)。 pa的路徑:4→1→8→4→5→null→5→6→1→8(第 9 步到相交節點 8);pb的路徑:5→6→1→8→4→5→null→4→1→8(第 9 步到相交節點 8);- 最終
pa == pb(都指向 8),返回該節點,符合預期
題友說:
“關于第二種解法發表下我的見解,統一長度說白了就是為了兩個鏈表向右對齊,打個比方listA長度為5,listB長度為6,不好比較,那就把前面補充成null(先這樣想)
listA=[null,4,1,8,4,5] listB=[5,6,1,8,4,5]
那這樣長度就一樣了,我們就能同時從開頭移動A和B進行比較。
那回到正常的思路,想A和B長度一樣,長度就都設置為A+B唄。那就往B最左邊補充A長度(5)個null,A最左邊補充B長度(6)個null。那就變成
listA=[null,null,null,null,null,null,4,1,8,4,5] listB=[null,null,null,null,null,5,6,1,8,4,5]
這樣長度一樣,好比較了吧,不過都是null,鏈表怎么移動啊,你就把A里面的6個null換成B的數據,B里面的null換成A的數據唄,反正都是要白白移動的,相交點在最后面,這樣補全是為了我們好操作鏈表。
那這樣理解的話這題就沒問題了。代碼是官方第二種解法的代碼。”
3 (未完待續)哈希集合解法:相交鏈表問題的另一種思路
這個解法還沒嘗試過。
除了之前討論的雙指針法,哈希集合也是解決相交鏈表問題的經典思路,其核心是通過存儲一個鏈表的所有節點,再遍歷另一個鏈表查找 “共同節點”,具體分析如下:
一、思路與算法邏輯
哈希集合的核心是利用 “集合元素唯一性” 的特性,將一個鏈表的節點全部存入集合后,通過檢查另一個鏈表的節點是否在集合中,判斷是否相交及找到相交節點。步驟如下:
- 存儲鏈表 A 的節點:遍歷鏈表
headA,將每個節點(注意是存儲節點本身,而非節點值)加入哈希集合visited。 - 查找鏈表 B 的節點:遍歷鏈表
headB,對每個節點執行判斷:- 若該節點在
visited中:說明此節點是兩個鏈表的 “第一個共同節點”(因為是從headB頭開始遍歷),直接返回該節點。 - 若遍歷完
headB所有節點都不在visited中:說明兩鏈表不相交,返回null。
- 若該節點在
二、代碼實現(Java)
java
運行
import java.util.HashSet;
import java.util.Set;/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {public ListNode getIntersectionNode(ListNode headA, ListNode headB) {// 哈希集合:存儲鏈表A的所有節點Set<ListNode> visited = new HashSet<ListNode>();ListNode temp = headA;// 第一步:遍歷鏈表A,將所有節點加入集合while (temp != null) {visited.add(temp);temp = temp.next;}// 第二步:遍歷鏈表B,查找集合中存在的節點temp = headB;while (temp != null) {if (visited.contains(temp)) {return temp; // 找到第一個相交節點,直接返回}temp = temp.next;}// 遍歷完B仍未找到,說明無相交return null;}
}
三、關鍵細節說明
- 存儲 “節點” 而非 “節點值”:
題目中明確 “值相同的節點可能是不同對象”(如示例 1 中 A 的 “1” 和 B 的 “1” 是不同節點),因此必須存儲節點的引用(地址),而非僅比較值,避免誤判。 - “第一個共同節點” 的必然性:
遍歷headB時,第一個在集合中找到的節點就是相交起點 —— 因為headB從頭部開始遍歷,且相交后的所有節點都在集合中,第一個匹配的節點即為最早的相交節點。 - 原始結構保留:
僅通過指針遍歷和集合存儲,未修改任何鏈表的next指向,滿足題目 “保持原始結構” 的要求。
四、復雜度分析
| 維度 | 分析 |
|---|---|
| 時間復雜度 | O (m + n):m 為headA長度,n 為headB長度,需各遍歷一次,無嵌套循環。 |
| 空間復雜度 | O (m):需存儲headA的所有 m 個節點,空間開銷隨headA長度線性增長。 |
五、與雙指針法的對比
| 對比維度 | 哈希集合法 | 雙指針法 |
|---|---|---|
| 時間復雜度 | O (m + n)(相同) | O (m + n)(相同) |
| 空間復雜度 | O (m)(需額外存儲一個鏈表) | O (1)(僅用兩個指針,最優) |
| 實現難度 | 邏輯直觀,易理解 | 需理解 “路程補償” 邏輯 |
若題目對空間開銷無嚴格限制,哈希集合法是更易想到的解法;若要求O (1) 空間(如進階要求),則雙指針法更優。




全解析2)

![[優選算法專題二滑動窗口——最大連續1的個數 III]](http://pic.xiahunao.cn/[優選算法專題二滑動窗口——最大連續1的個數 III])
)
)








的各種數據)

