題目鏈接

最大連續1的個數 III

題目描述

題目解析

問題本質

• 輸入：二進制數組nums（只包含 0 和 1）和整數k
• 操作：最多可以將k個 0 翻轉成 1
• 目標：找到翻轉后能得到的最長連續 1 的子數組長度

這個問題的核心是要找到一個區間，在允許翻轉最多k個 0 的情況下，這個區間內的 1（包括翻轉得到的 1）是最長的。

解題思路：滑動窗口法

滑動窗口（雙指針）是解決這類 "最長連續子數組" 問題的高效方法，基本思想是：

1. 用兩個指針left和right維護一個區間（窗口）[left, right]
2. 保證窗口內的 0 的數量不超過k（即可以通過翻轉使整個窗口都變為 1）
3. 不斷擴大窗口（移動right），當窗口不滿足條件時縮小窗口（移動left）
4. 記錄過程中出現的最大窗口長度

算法流程：

1. ?初始化： left = 0 , right = 0 , ret = 0 ；

2. ?當 right ?于數組??的時候，?直下列循環：

? ? ?i：進窗口，1無視，0計數表++；

? ? ?ii：判斷計數表是否 >k;

? ? ? ? ? 是則讓左側元素滑出窗?，更新哈希表的值，直到 0 的個數恢復正常；

? ? ?iii：更新結果，right++；

3. ?循環結束后， ret 存的就是最終結果。

關鍵代碼邏輯解析

// 當窗口中0的數量超過k時，需要縮小窗口
while(zero > k) {if(nums[left++] == 0) zero--;
}

這段代碼是算法的核心，它確保了窗口的合法性：

• 當 0 的數量超過 k 時，通過移動左指針縮小窗口
• 只有當移除的元素是 0 時，才減少zero的計數
• 循環結束后，窗口內 0 的數量一定≤k

ret = max(ret, right - left + 1);

這行代碼用于更新最長有效窗口的長度，每次移動右指針后都要檢查當前窗口是否是最長的。

完整代碼

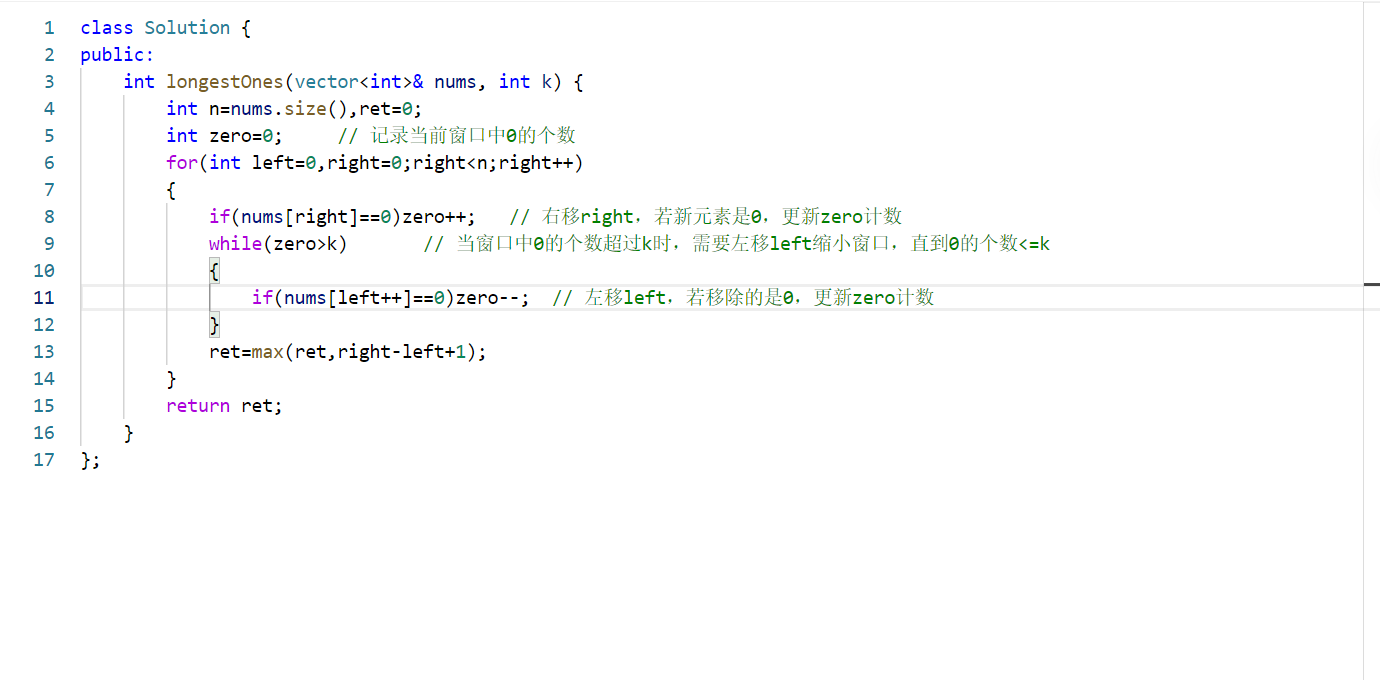
算法優勢分析

1. 時間效率：

   • 每個元素最多被left和right各訪問一次
   • 總時間復雜度為 O (n)，n 為數組長度
   • 相比暴力解法（嘗試所有可能的子數組）的 O (n2) 有顯著提升

2. 空間效率：

   • 只使用了常數個額外變量（left、right、zero、ret等）
   • 空間復雜度為 O (1)