引言

在機器學習的聚類任務中，K-means因其簡單高效廣為人知，但它有一個致命缺陷——假設簇是球形且密度均勻，且需要預先指定簇數。當數據存在任意形狀的簇、噪聲點或密度差異較大時，K-means的表現往往不盡如人意。這時候，DBSCAN（Density-Based Spatial Clustering of Applications with Noise） 作為基于密度的聚類算法，憑借其無需預設簇數、能識別噪聲、處理任意形狀簇的特性，成為工業界和學術界的神器

本文將從原理到代碼，帶你徹底搞懂DBSCAN，并通過實戰案例掌握其核心技巧。

一、DBSCAN核心概念：用“密度”定義簇

要理解DBSCAN，首先需要明確5個核心概念：

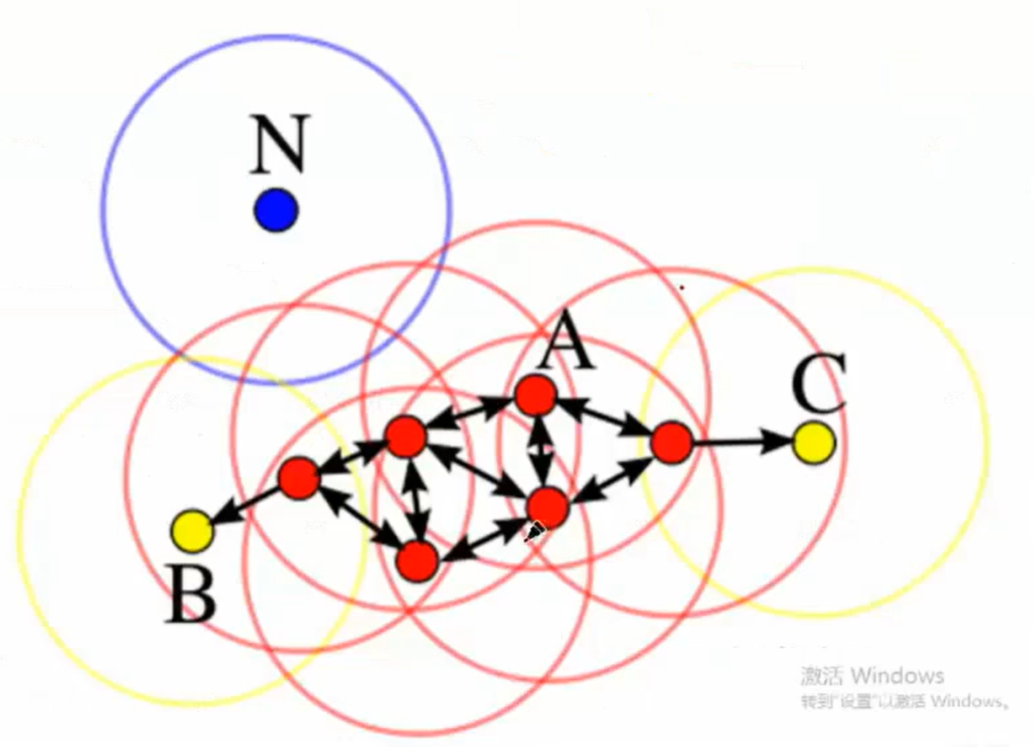
1. ε鄰域（ε-Neighborhood）

對于數據點 $p$，其ε鄰域是指所有與 $p$ 的距離不超過 $\epsilon$ 的點的集合，數學上表示為：
Nε(p)={q∈D∣distance(p,q)≤ε}N_\varepsilon(p) = \{ q \in D \mid \text{distance}(p, q) \leq \varepsilon \}Nε?(p)={q∈D∣distance(p,q)≤ε}
其中 $D$ 是數據集，$\text{distance}$ 常用歐氏距離（連續數據）或曼哈頓距離（高維稀疏數據）。

2. 核心對象（Core Object）

如果數據點 $p$ 的ε鄰域內至少包含 $\text{min\_samples}$ 個點（包括 $p$ 自己），則 $p$ 是一個核心對象。
換句話說，核心對象是“密度足夠高”的點，是簇形成的基礎。

3. 直接密度可達（Directly Density-Reachable）

如果點 $q$ 位于核心對象 $p$ 的ε鄰域內（即 $q\in N_{\epsilon }(p)$），則稱 $q$ 從 $p$ 出發是直接密度可達的。

4. 密度可達（Density-Reachable）

如果存在一個點序列 $p_1,p_2,...,p_n$，其中 $p_1=p$，$p_n=q$，且每個 $p_{i+1}$ 從 $p_i$ 直接密度可達，則稱 $q$ 從 $p$ 出發是密度可達的。
密度可達是直接密度可達的傳遞擴展，但不具備對稱性（即 $q$ 密度可達 $p$ 不代表 $p$ 密度可達 $q$）。

5. 密度相連（Density-Connected）

如果存在一個核心對象 $o$，使得 $p$ 和 $q$ 都從 $o$ 密度可達，則稱 $p$ 和 $q$ 是密度相連的。
密度相連的點屬于同一個簇。

6. 簇與噪聲

• 簇：數據集中最大的密度相連點集（即無法通過密度可達擴展更多點）。
• 噪聲：不屬于任何簇的點（不被任何核心對象密度可達）。

二、DBSCAN算法流程：從核心對象到簇的構建

DBSCAN的核心邏輯是“從核心對象出發，擴展密度可達的點形成簇”。具體步驟如下：

1. 計算所有點的ε鄰域：遍歷數據集，為每個點計算其ε鄰域內的點數量。
2. 篩選核心對象：保留那些ε鄰域內點數量 ≥ min_samples的點，標記為核心對象。
3. 擴展簇：從任意一個未被訪問的核心對象出發，遞歸地將其所有密度可達的點加入當前簇，并標記為已訪問。
4. 處理噪聲：所有未被訪問且不屬于任何核心對象的點，標記為噪聲。

三、代碼實戰：用Python實現DBSCAN

1. 環境準備與數據生成

我們使用 scikit-learn 提供的合成數據，并添加噪聲。首先安裝依賴：

pip install numpy pandas matplotlib scikit-learn

生成數據代碼：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs, make_noise
from sklearn.preprocessing import StandardScaler# 生成3個真實簇（含噪聲）
X, y_true = make_blobs(n_samples=300, centers=3, cluster_std=[1.0, 2.0, 0.8],  # 不同簇的密度差異random_state=42
)
X = StandardScaler().fit_transform(X)  # 標準化數據# 添加5%的噪聲點（偏離真實簇）
noise = make_noise(n_samples=int(0.05*len(X)), noise_scale=3.0, random_state=42)[0]
X = np.concatenate([X, noise])# 可視化原始數據
plt.scatter(X[:, 0], X[:, 1], c='gray', s=10, label='Unclustered Data')
plt.title("Raw Data with Noise")
plt.legend()
plt.show()

2. 使用scikit-learn的DBSCAN

sklearn.cluster.DBSCAN 已經封裝了高效的DBSCAN實現，我們直接調用并調參：

from sklearn.cluster import DBSCAN# 初始化DBSCAN，關鍵參數：eps=ε，min_samples=min_samples
dbscan = DBSCAN(eps=0.8, min_samples=5)
clusters = dbscan.fit_predict(X)  # 輸出：-1表示噪聲，其他為簇標簽# 統計結果
n_clusters = len(set(clusters)) - (1 if -1 in clusters else 0)  # 排除噪聲標簽-1
n_noise = np.sum(clusters == -1)
print(f"Estimated number of clusters: {n_clusters}")
print(f"Estimated number of noise points: {n_noise}")# 可視化聚類結果
plt.scatter(X[:, 0], X[:, 1], c=clusters, s=10, cmap='viridis')
plt.title(f"DBSCAN Clustering (eps=0.8, min_samples=5)")
plt.colorbar(label='Cluster ID (-1=Noise)')
plt.show()

3. 關鍵參數調優：如何選擇ε和min_samples？

DBSCAN的效果高度依賴兩個參數：

• eps（ε）：鄰域半徑，太小會導致很多簇被分割，太大可能合并不同簇。
• min_samples：核心對象的最小鄰域點數，通常設置為維度+1（如2維數據設為3-5）。

調參技巧：k-distance圖
k-distance圖通過計算每個點到其第k近鄰的距離并排序，繪制折線圖。曲線的“拐點”對應的距離即為合適的ε（通常k=min_samples-1）。

from sklearn.neighbors import NearestNeighbors
import numpy as np# 計算每個點的k近鄰距離（k=min_samples-1=4）
min_samples = 5
k = min_samples - 1
neighbors = NearestNeighbors(n_neighbors=k)
neighbors_fit = neighbors.fit(X)
distances, indices = neighbors_fit.kneighbors(X)# 排序距離并繪制
distances = np.sort(distances, axis=0)[:, 1]  # 取第k近鄰的距離（排除自己）
plt.plot(distances)
plt.xlabel("Points sorted by distance")
plt.ylabel(f"{k}-th Nearest Neighbor Distance")
plt.title("k-distance Plot for ε Selection")
plt.grid(True)
plt.show()

解讀k-distance圖：
曲線從左下到右上逐漸上升，當出現一個明顯的“跳躍”（拐點）時，對應的距離即為合適的ε。例如，若拐點在距離0.8處，則設置eps=0.8。

四、DBSCAN的優缺點與適用場景

優點：

• 無需預設簇數：自動根據數據密度劃分簇。
• 抗噪聲能力強：明確識別噪聲點（標簽-1）。
• 處理任意形狀簇：不依賴簇的球形假設。

缺點：

• 參數敏感：ε和min_samples的選擇對結果影響大。
• 高維數據效果下降：高維空間中距離度量失效（維度詛咒）。
• 密度不均勻時表現差：若簇間密度差異大，難以找到統一的ε。

適用場景：

• 數據分布有明顯密度差異（如用戶分群中的高價值/低活躍用戶）。
• 存在噪聲或離群點（如金融欺詐檢測）。
• 簇形狀不規則（如地理區域的用戶分布）。

五、總結

DBSCAN是一種強大的密度聚類算法，核心是通過“核心對象”和“密度可達”定義簇，天然抗噪聲且能處理任意形狀的簇。實戰中需重點調參ε和min_samples，推薦使用k-distance圖輔助選擇ε。下次遇到傳統聚類算法無法解決的復雜數據時，不妨試試DBSCAN